双向S-属性粗糙集及其性质
郭志林
双向S-属性粗糙集及其性质
郭志林
(商丘师范学院数学系,河南商丘476000)
针对S-粗糙集中元素的动态特性,在属性集及属性测度理论基础上,提出了双向S-属性粗糙集的概念,讨论了双向S-属性粗糙集的性质,并就双向S-属性粗糙集的精度进行了讨论.
双向S-粗糙集;属性集;属性测度;粗糙集;粗糙度
Pawlak粗糙集模型[1,2]的一个局限性是它所处理的分类必须是完全正确的或是肯定的.因为它是严格按照等价类来分类的,因而它的分类是精确的,即“包含”或“不包含”,而没有某种程度上的“包含”或“属于”,所以粗糙集扩展模型的研究已成为粗糙集理论新的研究热点[3,4].Z.Pawlak粗糙集只是研究了系统的静态特性.针对具有动态特性的集合X⊂U,史开泉教授在文[5]中提出了S-粗糙集(singular rough sets),给出了S-粗糙集的两类结构,对S-粗糙集的特性和应用给出了进一步的讨论[5-9].在粗糙集模型中,论域U上的任意一个经典集合A不一定能用知识库(U,R)中的知识来精确的描述,这时就用A关于(U,R)的一对上下近似来描述.但在实际生活中人们涉及的知识或概念往往是模糊的不确定的,我们只能确定它具有某些属性.这样,对于对象空间U的一个对象x和属性集R上的属性集合A,我们不能简单地说x是“绝对”属于A还是不属于A,而只能说x在多大程度上属于A.这时用它的属性来描述就显得非常方便.本文根据程乾生教授提出的属性数学[10,11]的有关概念,结合元素的动态特性,在文献[12]的基础上,提出了双向S-属性粗糙集的概念,建立了双向S-属性粗糙集的数学模型,就满足不同属性测度要求的属性集,给出带参数α,β[13]的双向S-属性粗糙集模型.并讨论了双向S-属性粗糙集的性质.
1 预备知识
1.1 双向S-粗糙集
定义1.1.1[5]给定U,F是定义在U上的元素迁移族,称X**⊂U是U上的双向奇异集合(t wo direction singular sets),简称双向S-集合,如果f,¯f∈F,而且

其中X′=X{x|x∈X,¯f(x)=u∈X}称作X的亏集,={x|x∈X,¯f(x)=u∈X}是X⊂U的¯f-萎缩.
这里,X是Z.Pawlak粗糙集(R-(X),R-(X)中的集合,X⊂U;“萎缩”一词的意义是:集合X中的元素得到删除,X变成,中元素的个数少于X中元素个数,Card() 定义1.1.2[5]设X**是U上的双向S-集合,称(R,F)o(X**)是X**的下近似,如果 称(R,F)o(X**)是的X**上近似,如果称集合对((R,F)o(X**),(R,F)o(X**))是X**⊂U的双向奇异粗糙集(two direction singular rough sets),简称双向S-粗糙集. 称bnR(X**)是X**⊂U的边界,而且 关于双向S-粗糙集的意义及应用请参考文献[5-9]. 1.2 属性集与属性可测空间 定义1.2.1[10,11]设U是研究对象的全体,称为对象空间,X为U中元素的某类属性,称为属性空间或最大属性集,属性空间X的任一子集A称为属性集. 属性集A与普通集合具有类似的运算法则,详细内容请参考文献[10,11].定义1.2.2[10,11]设R为X上的一些属性集所组成的集合,如果R满足(1)如果A∈R,则¯A∈R;(2)如果A∈R,B∈R,则A∪B∈R,那么,称R为属性代数,如果属性代数R还满足:∀Ai∈R,i=1,2,…,有∪iAi∈R,则称R为属性σ代数,称(X,R)为属性可测空间. 定义1.2.3[10,11]设x为X中的一个元素,A为一个属性集,μA(x)表示“x具有属性A”的程度,称为x∈A的属性测度(0≤μA(x)≤1). 定义1.2.4[10,11]设(X,R)为属性可测空间,称μ(x)为(X,R)上的属性测度,如果 (1)μA(x)≥0,∀A∈R;(2)μX(x)=1;(3)若Ai∈R,Ai∩Aj=Ø(i≠j),则μ μ(x))为属性测度空间. 设U为对象空间,(X,R,μ(x))为属性测度空间.X**是R⊂X上的双向S-集合,按定义,∀x∈U,0≤μx(X**)≤1.若μx(X**)=0,则认为x完全不属于X**,若μx(X**)=1,则认为x完全属于X**,若0<μx(X**)<1,则说x依测度μx(X**)属于X**,这时在完全属于X**和完全不属于X**之间呈现出一种中间的过度状态.有时,我们需要研究满足一定的属性测度要求的属性集的性质,由此,我们给出带参数α,β[13]的双向S-属性粗糙集模型. 定义2.1 设U为对象空间,(X,R,μ(x))为属性测度空间. X**是R⊂X上的双向S-集合,则X**关 其中[x]R为元素x在属性R下的等价类.若XR**(x)=X¯R**(x),则称X**是可定义的,否则称X**是属性粗糙集(attribute rough sets),称X¯R**(x)是X**关于(X,R,μ(x))的正域,称~X¯R**(x)是关于(X,R,μ(x))的负域,称X¯R**(x)∩(~X¯R**(x))为X**的边界(~X¯R**(x)为X¯R**(x)的补集). 当属性R比较明确时,我们将下标R取掉,XR**(x)简记为X**,X¯R**(x)简记为X¯**. 定理2.1 设(X,R,μ(x))为属性测度空间.X**,Y**是R⊂X上的双向S-集合,由定义2.1给出的下近似和上近似具有下列性质: 证明 我们只证明前半部分性质,后半部分性质类似可证明. (1)显然. (6)由定义2.1,显然. 定义2.2 设(X,R,μ(x))为属性测度空间,X**是R⊂X上的双向S-集合,定义X**关于(X,R,μ(x))的粗糙度为ρR(X**),如果 当|¯X**|=0时,约定ρR(X**)=0; 显然,0≤ρR(X**)≤1,0≤ηR(X**)≤1. 若X**是可定义的,则ρR(X**)=0,ηR(X**)=1. 定义2.3 设U为对象空间,(X,R,μ(x))为属性测度空间. X**是R⊂X上的双向S-集合,则X**关于属性测度空间(X,R,μ(x))依参数0≤β<α≤1的下近似(R,F)o(X*(α*))和上近似(R,F)o(X*(β*))分别定义为 若(R,F)o(X*(α*))=(R,F)o(X*(β*)),则称X**关于属性测度空间(X,R,μ(x))依参数α,β是可定义的,否则称X**是不可定义的或依参数α,β的属性粗糙集. X**关于属性空间(X,R,μ(x))依参数α,β的正域、负域和边界分别定义为 (R,F)o(X*(α*))可以解释为U中肯定属于属性集X**的属性测度不小于α的那些对象的全体,(R,F)o(X*(β*))可解释为U中可能属于属性集X**的属性测度不小于β的那些对象的全体.显然 这样,(R,F)o(X*(α*))又可以解释为U中肯定属于属性集X**的属性测度不小于α的那些对象所在属性类的并集,(R,F)o(X*(β*))可解释为U中可能属于属性集X**的属性测度不小于β的那些对象所在属性类的并集. 定义2.4 设U为对象空间,(X,R,μ(x))为属性测度空间.X**是R⊂X上的双向S-集合,对于0≤β<α≤1,定义X**关于参数α,β的粗糙度ρ(X**,α,β)为 当|(R,F)o(X*(β*))|=0时,约定ρ(X**,α,β)=0. 定理2.2 当X**为经典集合时,∀α,β∈(0,1],(R,F)o(X*(α*))和(R,F)o(X*(β*))分别退化为X**在Pawlak意义下关于(U,R)的下近似RX**和上近似R¯X**. 证明 ∀α∈(0,1],由于X**是经典集合,因此μX**(x)∈{0,1},从而 同理可证(R,F)o(X*(β*))=R¯X**. 性质3.1 设(X,R,μ(x))为属性测度空间.X**,Y**是R⊂X上的双向S-集合,则对于参数0≤β<α≤1有 证明 由定义2.3和定理2.1直接可得. 由定义2.3容易得到 性质3.2 (1)0≤ρ(X**,α,β)≤1, (2)若β固定,则ρ(X**,α,β)随α增加而增加,若α固定,则ρ(X**,α,β)随β增加而减少. 性质3.3 设U为对象空间,(X,R,μ(x))为属性测度空间.X**,Y**是R⊂X上的双向S-集合,且X**⊆Y**,0≤β<α≤1,则 (1)若(R,F)o(X*(β*))=(R,F)o(Y*(β*)),则ρ(Y**,α,β)≤ρ(X**,α,β), (2)若(R,F)o(X*(α*))=(R,F)o(Y*(α*)),则ρ(X**,α,β)≤ρ(Y**,α,β). 证明 由性质3.1(4)知(R,F)o(X**(α))⊆(R,F)o(Y**(α))且(R,F)o(X**(β))⊆(R,F)o(Y**(β)) 从而由定义2.4即得(1),(2)成立. 性质3.3说明由X**⊆Y**不能简单的判别ρ(X**,α,β)和ρ(Y**,α,β)的大小. 性质3.4 设U为对象空间,(X,R,μ(x))为属性测度空间.X**,Y**是R⊂X上的双向S-集合,0≤β< α≤1,则 证明 由性质3.1知 由于对于任意的有限集A,B有 从而 设S也是X上的一些属性集所组成的集合,其构成的属性测度空间为(X,S,μ(x)).若双向S-集合X**关于属性测度空间(X,S,μ(x))的上、下近似分别记为(x)和(x),依参数0≤β<α≤1的下近似和上近似分别记为(R,F)(X)和(R,F)(X),记ρS(X**,α,β)和ρR(X**,α,β)分别为X**关于属性测度空间(X,S,μ(x))和(X,R,μ(x))中关于α,β的粗糙度,则有 性质3.5 若S⊆R.X**是S⊂R⊆X上的双向S-集合,0≤β<α≤1,则 性质3.6 若S⊆R,X**是S⊂R⊆X上的双向S-集合,则 (1)ρS(X**)≤ρR(X**), (2)ρS(X**,α,β)≤ρR(X**,α,β). (2)由性质3.5(2)有, 从而由定义2.4, 性质3.6说明划分越细,所得近似的粗糙度越小.由此,我们可以通过调整参数α,β的取值,或是通过对对象空间划分的加细来减少属性集合的粗糙度,从而使问题的解决更灵活更贴近实际. 本文针对双向S-粗糙集的动态特征,将双向S-粗糙集与属性可测理论结合起来,得到了双向S-属性粗糙集模型及依参量的双向S-属性粗糙集模型,并对参量的不同取值讨论了粗糙度的不同变化情况,从而说明双向S-粗糙集是对Pawlak粗糙集和S-粗糙集的进一步完善和补充,为动态属性决策提供了理论论据.限于篇幅,我们将在后继文章中继续讨论不同参数α,β对双向S-属性粗糙集的影响以及这种模型下集合的相对可辨别性、属性的近似依赖性等. [1] PAWLAK Z.Rough Sets[J].International Journal of International Sciences,1982,11:341-356. [2] PAKLAK Z,SKOWRON A.Rudi ments of Rough Sets[J].Infor m ation Sciences,2007,177:3-27. [3] PAWLAK Z,SKOWRON A.Rough Sets:Some extensions[J].Infor m ation Sciences,2007,177:28-40. [4] YAO Y Y,ZHAO Y.Attribute Reduction in Decision Theoretic Rough SetModels.Information Sciences,2008,178(17):3356-3373. [5] 史开泉,崔玉泉.S-粗糙集和它的一般结构[J].山东大学学报(理学版),2002,37(6):471-474. [6] SH I Kaiquan.S-rough Sets and Application in Diagnosis-recognition forDisease[J].IEEE Proceedings of the First International Conference on M achine Learning and Cybem etics,2002,4(1):50-54. [7] 史开泉,姚炳学.函数S-粗糙集与规律辨识[J].中国科学E:信息科学,2008,38(4):553-564. [8] 史开泉,赵建立.函数S-粗糙集与规律安全-认证[J].中国科学E:信息科学,2008,38(8):1234-1243. [9] 史开泉,崔玉泉.S-粗糙集与粗决策[M].北京:科学出版社,2006. [10] 程乾生.属性集和属性综合评价系统[J].系统工程理论与实践,1997,9:1-9. [11] 程乾生.属性识别理论模型及其应用[J].北京大学学报(自然科学版),1997,33(1):12-20. [12] 郭志林.属性测度空间的粗糙集模型[J].模糊系统与数学,2009,23(2):162-166. [13] 张文修,吴伟志,梁吉业,等.粗糙集理论与方法[M].北京:科学出版社,2005. Two-direction Singular Attribute Rough Sets and It′s Properties GUO Zhi-lin Considering the dynamic characteristics of the elements in rough sets,two direction singular attribute rough setsmodel is presented based on the theory of attribute sets and attribute measure.Moreover,the properties of the two direction singular attribute rough sets,the precision of it is discussed. t wo direction singular rough sets;attribute sets;attribute measure;rough sets;roughnessmeasure O159 A 2009-12-01; 2010-09-05 河南省自然科学基金(092102210152);河南省政府政策研究招标课题(B373) 郭志林(1963-),男,回族,副教授,研究方向为粗糙集理论及应用.E-mail:guozhilin112@126.com
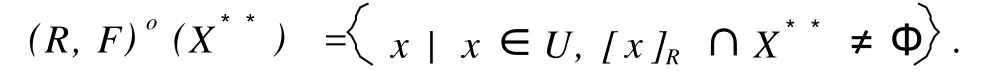
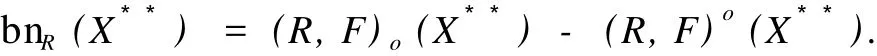
2 双向S-属性粗糙集
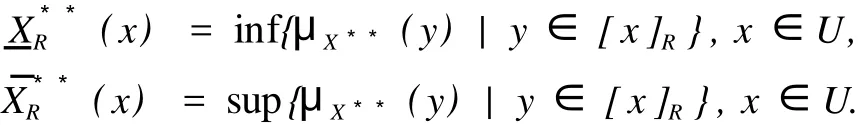
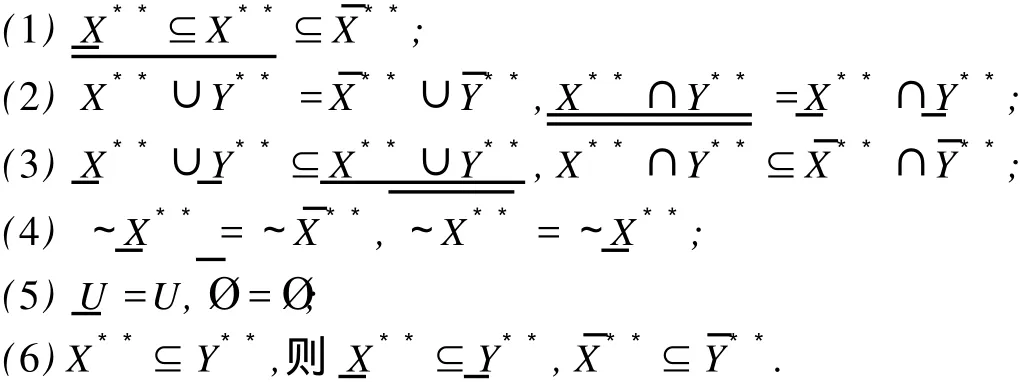
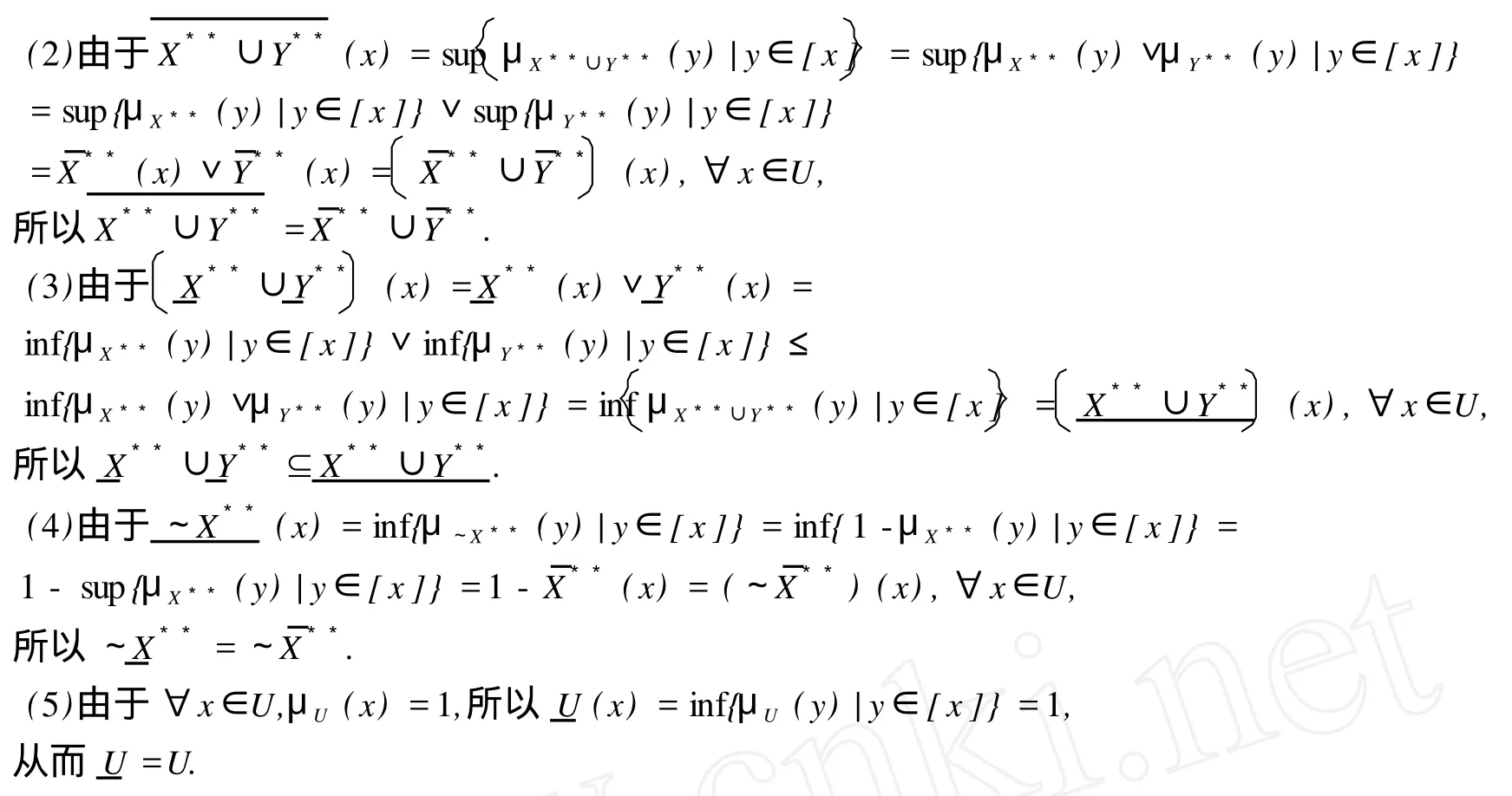
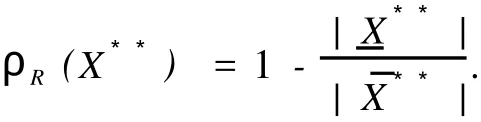
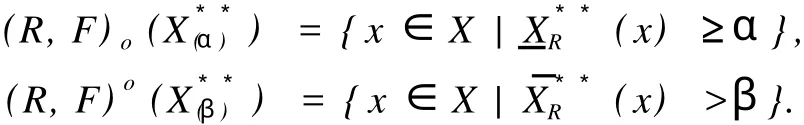
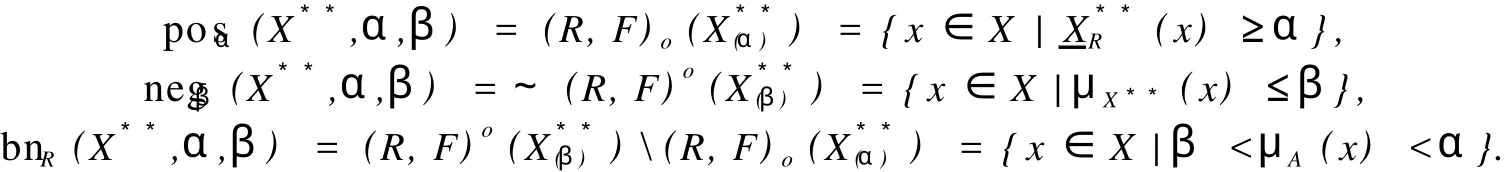
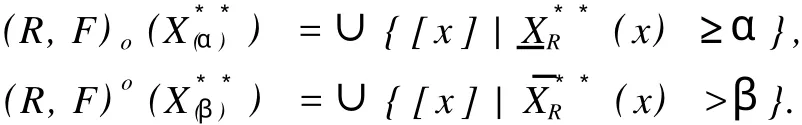
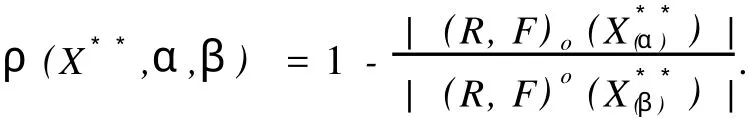
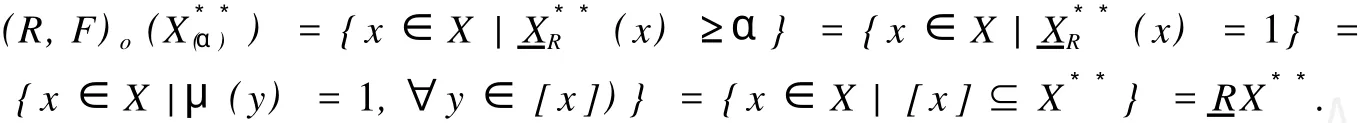
3 双向S-属性粗糙集的性质
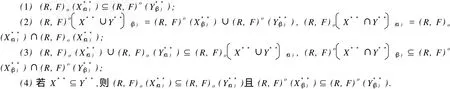
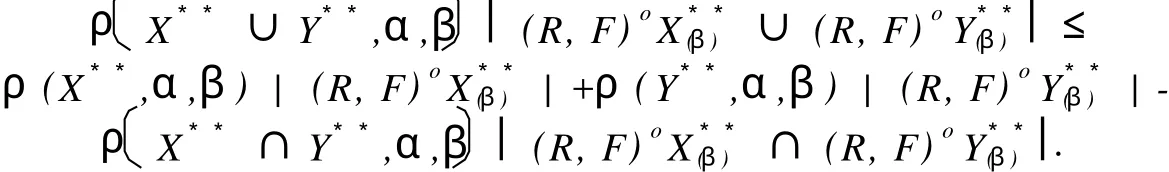
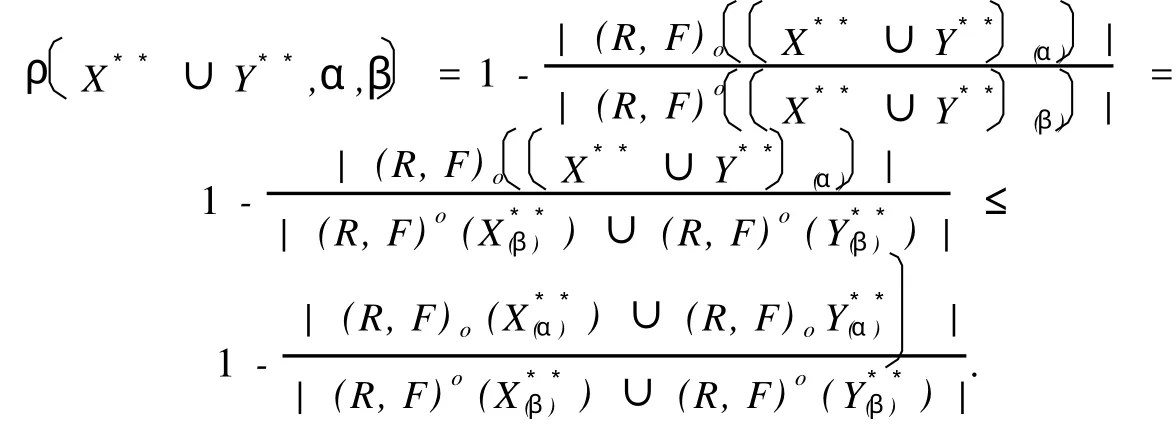
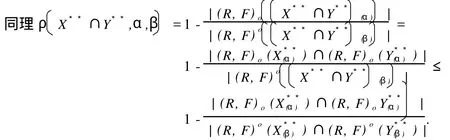
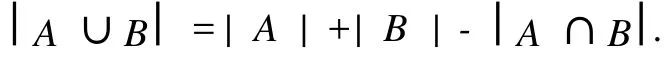
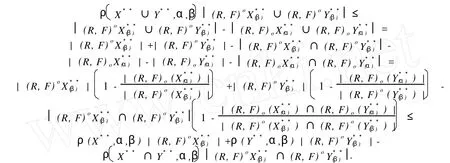



4 结束语
(Departm ent ofM athematics,Shangqiu Nor mal College,Shangqiu476000,China)

