基于小波理论与混沌矩阵的图像加密技术

朱敏慧

基于小波理论与混沌矩阵的图像加密技术

朱敏慧

(西安工程大学理学院,陕西西安710048)

提出了一种基于小波变换以及混沌序列的快速图像加密算法.利用小波变换(DWT)的基本原理,对秘密图像以及由混沌序列生成的广义混沌图像进行小波变换,然后把小波变换后系数进行融合,最后利用小波逆变换进行图像重构得到结果图像.数值试验表明该算法简单易行,抗攻击能力较强.

小波变换;信息加密;置乱;混沌序列

随着多媒体和互联网技术的飞速发展,通过网络对媒体信息产品进行下载、复制、转售和编辑,甚至恶意对信息进行篡改与破坏,使数字媒体作品的安全问题日益突出,而使用密码对图像进行加密是最有效的办法.其中数字水印[1-3]和图像加密[4-6]是目前研究最为广泛的领域.

混沌是一种非线性动力学规律控制的行为,表现为对初始值和系统参数的敏感性、白噪声的统计特性和混沌序列的遍历特性,其吸引子的维数是分维,有十分复杂的分形结构,具有不可预测性.由于混沌序列有如此优良的特性,从20世纪80年代末,混沌开始被应用于保密通信领域,其中尤其受密码学界重视的是混沌序列密码方法.用混沌加密方法能极大地简化传统序列密码的设计过程.在利用计算机生成混沌序列时,由于计算机有限精度效应,生成的混沌序列最终将退化为周期序列,从而影响到信息加密的安全.为了提高利用混沌序列进行加密的算法的安全性,常见的解决方案是进行多重混沌加密,但这样增加了运算量,会影响到加密的效率.

小波分析是近20年发展起来的新兴学科,是当前数学领域中迅猛发展的一个新方向,具有丰富的数学理论意义和广泛的工程应用价值.从数值分析的角度看,它是Fourier分析的一个突破性进展,给许多相关学科的研究带来了新思想,也为图像处理领域提供了一种更有效的分析工具[7,8].小波变换之所以在图像处理领域具有巨大优势,是因为小波变换是一个强有力的多分辨率分析工具,人眼视觉的生理和心理实验表明:图像的小波多分辨分解与人眼视觉的多通道分解规律一致,另外,小波变换的低嫡性、去相关性和选基灵活性等特点,也为其成功应用于该领域提供了天然优势.由于小波理论本身的研究日趋完善,小波多尺度分析方法的应用愈来愈广泛,尤其是在信号和图像处理中良好的时频特性,使得小波域中的信息加密技术成为近年来的研究热点.

本文给出了一种基于小波变换和混沌序列的数字图像加密算法,数字实验表明:该方法思想简单易于实现,加密效果较好,抗攻击性较强,安全性较好.

1 基本原理

1.1 离散小波变换(DWT)

所谓小波,即存在于一个小区域的波.其数学定义是:设ψ(t)为一平方可积函数,即ψ(t)∈L2(R),若其Fourier变换ψ(ω)满足:则称为一个基本小波或小波母函数,并称上式是小波函数的可容许条件.

将小波母函数ψ(t)进行伸缩和平移,设其伸缩因子(又称尺度因子)为a.平移因子为τ,令其平移伸缩后的函数为ψa,τ(t),则有

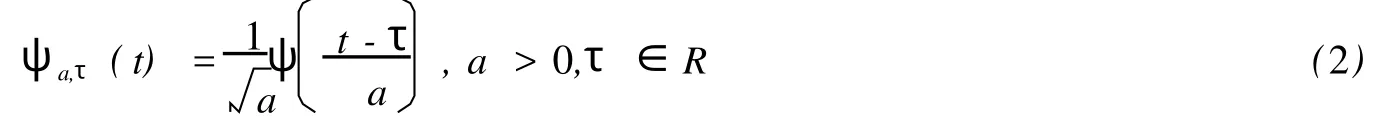
称ψa,τ(t)为依赖于参数a,τ的小波基函数.由于尺度因子a、平移因子τ是连续变化的值,因此ψa,τ(t)为连续小波基函数.它们是由同一母函数ψ(t)经伸缩和平移后得到的一组函数系列.

将L2(R)空间的任意函数f(t)在小波基下展开,称其为函数f(t)的连续小波变换CWT,变换式为:

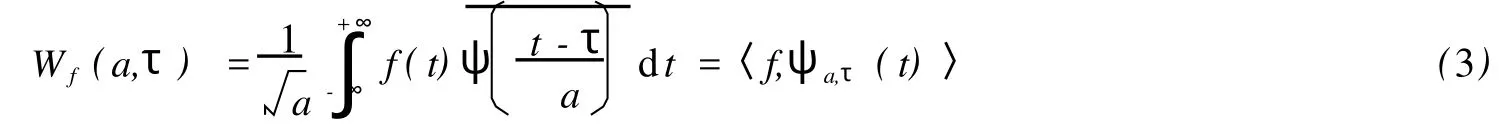
任何变换都必须存在逆变换(亦称反变换)才有实际意义.对连续小波变换而言,可以证明,若采用的小波满足可容许性条件,则其逆变换I CWT存在,也即根据信号的小波变换系数就可精确地恢复原信号,并满足下述连续小波变换的逆变换公式:

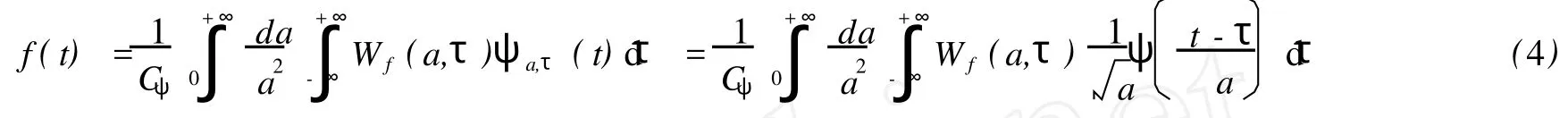
由连续小波变换的概念知道,在连续变化的尺度a及时间τ值下,小波基ψa,τ(t)具有很大的相关性,因此信号f(t)的连续小波变换系数的信息量是冗余的.实际运用中,很多情况下,需要考虑的是压缩数据及节约计算量,如在图像压缩、数值计算等领域,希望在不丢失原信号信息的情况下,尽量减小小波数的冗余度.因此有必要讨论连续小波ψ(a,τ)和连续小波变换Wf(a,τ)的离散化,也就是针对连续的尺度参数a和连续平移参数τ进行离散化.在连续小波中,考虑函数:

在离散化时,通常对尺度按幂级数进行离散化,即取a=am0,(m为整数,a0≠0,一般取a0=2),并且相应的位移间隔取2mTs得到的离散小波函数:

于是,任意函数f(t)的离散小波变换DWT为:

DWT与CWT不同,在尺度-位移相平面上,它对应一些离散的点,因此称之为离散小波变换.

如图1形象地表示了图像的两层小波分解.可以看出,图像在每一个分解层上都被分解成四个频带,分别为LL,LH,HL,HH;接着下一层分解只仅仅对低频分量LL进行分解.因此利用小波变换,图像被分解成逼近图像和细节图像之和,可认为它是一个将图像在相互垂直的空间频率上进行变换的过程.离散小波变换在提取图像低频信息的同时,又获得了3个方向的高频边缘细节信息.

图1 图像的两层小波分解Fig.1 2-levelwavelet decomposition of image

1.2 混沌系统[9]

以典型的Logistic混沌映射作为生成混沌序列的混沌系统,Logistic映射表示为:

通过实验发现,当3.569946…≤μ≤4,Logistic映射的输入和输出都分布在区间(0,1)上,且工作处于混沌状态,即此时由初始条件x0在Logistic映射的作用下所产生的序列{xk,k=0,1,2,…}具有非周期的、不收敛并对初始值非常敏感的性质.

Logistic映射经过一定次数的迭代后,在线段(0,1)上分布了大量的混沌点,其概率密度ρ(t)的解析表达式为

式(9)为Chebyshev分布.

1.3 基于n次Bézier曲线构造广义混沌序列

n次Bézier曲线为

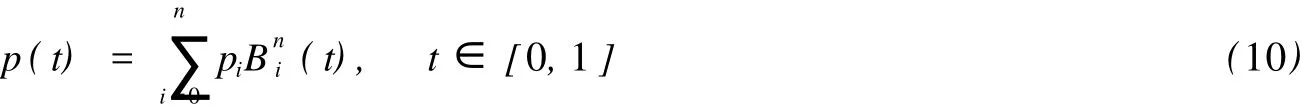
其中Bni(t)为n次Bernstein基函数,p0,p1,…,pn为控制点.

假定已给n+1个混沌序列{a1i,a2i,…,ani,…}(i=1,2,…,n+1),其中上标i表示第i个混沌序列,则利用n次Bézier曲线构造的广义混沌序列为:

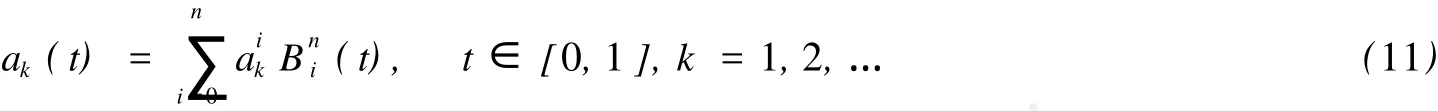
其中t为参数.相应的广义混沌序列的混沌动力学方程为:

其中F(＊)表示生成混沌映射.

根据式(8)、(11)可以在已知的混沌序列的基础上,生成混沌矩阵C I.具体方法如下:给定初值μi和, i=1,2,…n+1,由公式(11)经过N-1次混沌迭代运算得到混沌实值序列α1,α2,…,αN,通过排序变换将这N个值由小到大排序,生成β1,β2,…,βN,并确定αi在β1,β2,…,βN中的位置编号,形成地址集合G1={g1, g2,…,gN},反复操作M次,便生成混沌矩阵C I:

1.4 加密算法

Step1:输入n,密钥αi、μi(i=1,2,…,n)和t,其中n为混沌序列的个数,αi、μi(i=1,2,…,n)为每一个混沌序列的初始值,t为参数;

Step2:输入密钥α0,其中α0为融合参数;

Step3:利用式(8)、(11)可以在已知的混沌序列的基础上,生成混沌图像C I;

Step4:对秘密图像SI和混沌图像CI进行小波变换,分别得到SI的小波变换系数SLLC,SLHC,SHLC, SHHC和CI的小波变换系数CLLC,CLHC,CHLC,CHHC;

Step5:对Step4中所得的SI的小波变换系数和CI的小波变换系数利用融合系数α0进行融合;

Step6:利用小波逆变换对Step5所得的融合结果进行重构得到结果图像EI.

1.5 恢复算法

Step1:输入n,密钥α0、αi、μi(i=1,2,…,n)和t;

Step2:利用式(8)、(11)可以在已知的混沌序列的基础上,生成混沌图像C I;

Step3:对结果图像EI和混沌图像CI进行小波变换,分别得到EI的小波变换系数ELLC,ELHC, EHLC,EHHC和C I的小波变换系数CLLC,CLHC,CHLC,CHHC;

Step4:对Step3中所得的EI的小波变换系数和C I的小波变换系数利用密钥α0进行融合逆运算;

Step5:利用小波逆变换对Step4所得的结果进行重构得到恢复图像R I.

2 试验结果与分析

2.1 数字图像加密和恢复实例

图2基于本文算法给出数字图像加密和恢复的实例:其中Lena图(256×256)为秘密图像;利用三个混沌序列及二次有理Bezˊier曲线生成混沌矩阵,密钥分别为:n=2,α0=0.1,α1=0.1,μ1=4,α2=0.2,μ2= 3.9,α3=0.3,μ3=3.8,t=0.4;对秘密图像Lena图和生成的混沌图像C I应用Daubecchies小波变换(db1).

图2 数字图像加密和恢复实例Fig 2 Encryption of digital i mage and example of restoration

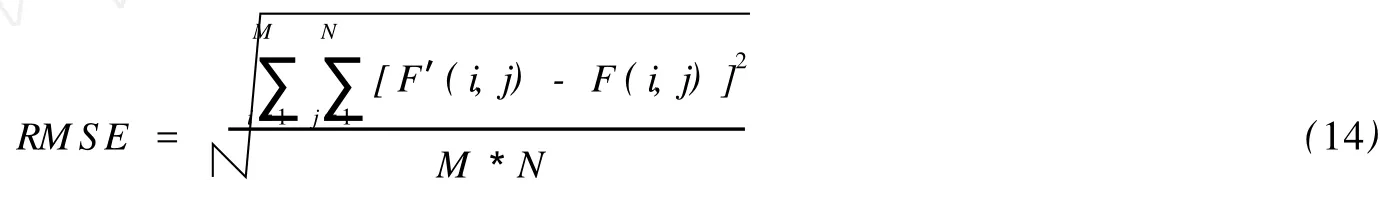
其中,Fi,j、Fi,′j分别表示原始图像和恢复图像(i,j)位置处的像素值,且1≤i≤M,1≤j≤N.RMSE越小,说明两幅图像越相像.

2.2 客观评价准则

传统的客观评价方法用恢复图像偏离原始图像的误差来衡量恢复图像的质量,最常用的有均方根误差(RMSE:RootMean Squared Error)和峰值信噪比(PSNR:Peak Signal to Noise Ratio)[10].

RMSE的表达式为

PSNR的表达式为

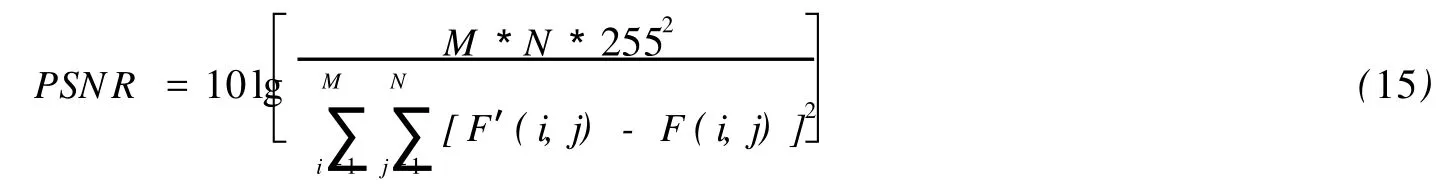
单位是dB,峰值信噪比PSNR越大,说明图像的保真度越好,两幅图像越相似. PSNR本质上与RMSE相同,其关系表达式为

利用本文算法恢复图像与原始秘密图像的峰值信噪比PSNR为78.36,由此可知两幅图像的保真度较好,两幅图像非常像;RMSE为均方根误差0.795 4,从而可以得出算法的恢复效果较好.

2.3 密钥空间分析

从基于2次Bézier曲线构造广义混沌序列的过程可以看出应用于数字图像加密的密钥有9个,大大提高了加密的安全性;更进一步如果利用K个混沌序列生成广义混沌序列并应用于数字图像加密时密钥会达到2K+1+1个之多;另外,可以利用不同的混沌序列生成混沌矩阵.

从效率方面分析,生成混沌矩阵的算法时间复杂度均为O(M×N),这说明采用广义的混沌序列加密时,不会提高算法的时间复杂度.

2.4 噪声攻击

图像在传输过程中,常常受到某种干扰而含有各种噪声.图3a和图3b为分别对含秘密图像添加了密度为0.5%和1%的高斯噪声后进行图像恢复的结果;图4a和图4b为对含水印图像添加了0.5%和1%椒盐噪声后进行图像的结果从结果,可以看出,本文算法高斯噪声和乘性噪声具有较好的稳健性.

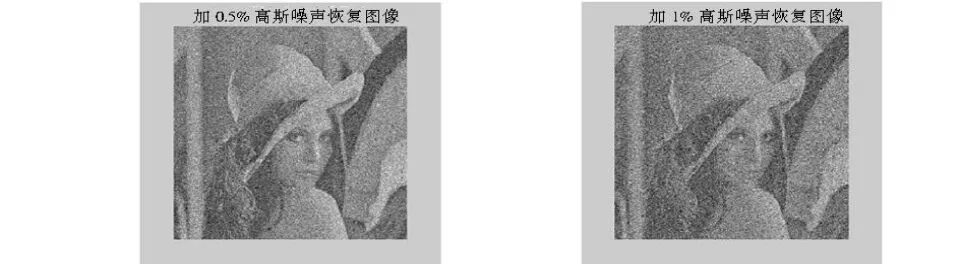
图3 对结果图像添加高斯噪声后的恢复图像Fig 3 I mage of restoration which increasing Gauss noise of result image

图4 对结果图像添加椒盐噪声后的恢复图像Fig 4 I mage of restoration which increasing salt noise of result i mage

2.5 密钥敏感性分析

3 结论

本文给出了一种基于小波变换和混沌图像的数字图像加密算法,该算法思想简单,易于编程,具有较好的安全性,且恢复图像质量较高.另外可以利用不同的混沌系统生成混沌图像、且融合参数α0可以利用混沌序列,以增加密钥空间.

[1] KUMSAWAT P,ATTKIT MONGCOL K,SR IKAEW A,SUJ ITJORN S.Wavelet-based I mageWatermarkingUsing the Genetic Algorithm[C]//Knowledge-based Intelligent Information Andengineering Systems.8th International Conference,KES2004.Proceedings(Lecture Notes in Artificial IntelligenceVol.3215),2004,3:643-649.

[2] BAO P,MA Xiao-hu.I mage Adaptive Watermarking UsingWaveletDomain Singular Value Decomposition[J].IEEE Trans.on Circuits and System s forV ideo Technology,2005,15(1):96-102.

[3] 丁志中,梁秋娟.一种具有良好鲁棒性的彩色图像水印算法[J].中国科学技术大学学报,2010,40(2):172-177.

[4] 熊绍强.一种基于混沌变换的图像加密算法[J].重庆科技学院学报,2009,11(6):139-141.

[5] ZHANGLin-hua,L I AO Xiao-feng,WANG Xue-bing.An I mage Encryption Approach Based on ChaoticMaps[J].Chaos,Solitons and Fractals,2005,24(3):759-765.

[6] 孙秋冬,顾永杰,马文新,等.基于小波变换的数字图像双重随机置乱加密[J].上海第二工业大学学报,2008,25(4): 271-275.

[7] 徐 晨,赵瑞珍,甘小冰.小波分析一应用算法[M].北京:科学出版社,2004.

[8] 葛哲学,沙 威,等.小波分析理论与MATLABR2007实现[M].北京:电子工业出版社,2007.

[9] 李昌刚,韩正之,张浩然.一种基于随机密钥及“类标准映射”的图像加密算法[J].计算机学报,2003,26(4):465-470.

[10] 孙兆林.MATLAB 6.X图像处理[M].北京:清华大学出版社,2002:192-197.

Technology of I mage Encrypting Based on Wavelet and Chaotic

ZHU Min-hui
(School of Science,Xi’an Polytechnic University,Xi’an710048,China)

A quckly image encrypting algorithm based on wavelet transfor mation and chaos sequence is introduced. Firstly,the secret image is scrambled.Secondly,the secret image and the chaotic image generated by extended chaotic sequence are decomposed into low-frequency and high-frequency images,then the wavelet coefficients are calculated,the fused wavelet coefficients are composed,and the fusion image is got by inverse wavelet transfor mation. Finally,the performance of the fusion algorithm is evaluated and analysed.The experimental results show that the proposed method is simple and viable.

wavelet transformation;information enryption;scrambling;chaotic sequence

TN911.73

A

0253-2395(2010)04-0533-05

2010-04-18;

2010-05-21

国家自然科学基金(10671155);西安工程大学校管科研资助项目

朱敏慧(1977-),女,陕西富平人,讲师.E-mail:xiao-zhu123@sohu.com