一类离散Hamilton系统指定最小周期的次调和解
肖华峰
一类离散Hamilton系统指定最小周期的次调和解
肖华峰
(广州大学数学与信息科学学院,广东广州510006)
文章研究了一类离散Hamilton系统次调和解的存在性.通过使用一种分解技巧,估计周期解的最小周期对应泛函的能量,得到Hamilton系统指定最小周期的次调和解存在性的一些充分条件.把这些充分条件应用到离散单摆方程中,可以得到单摆方程次调和解存在性的一些充分条件,改进了已有文献中的结果.
临界点;次调和解;指定最小周期;离散Hamilton系统
0 引言
一方面,差分方程被视为微分方程的离散形式,可以用来逼近微分方程.另一方面,在研究计算机、经济学神经网络、生态学及控制论等学科过程中出现了大量的差分方程,这就需要对差分方程进行更深入和广泛的研究,在过去几十年里,许多学者研究了差分方程的定性性质,如非共轭性、稳定性、吸引性、振荡性和边值问题[1,3].但是,对于差分方程周期解的研究,结果还是相对较少,其原因是缺乏有效的工具.2003年,郭志明、庾建设首次应用变分方法来研究差分方程的周期解[5,6],为了应用临界点理论来研究差分方程,他们建立了一个变分框架,然后把二阶差分方程的周期解的存在性问题转化成为对应变分泛函的临界点的存在性的问题.此后,差分方程周期解的研究成果不断涌现.例如,对差分方程边值问题的研究可以参考[11,14],对周期解的研究可以参考[2,5,6,7,9,12],对同宿轨的研究可以参考[4,8,13],对异宿轨的研究结果相对较少①XI AO H F,YU J S.Heteroclinic Orbits for a Discrete Pendulum Equation[J].J D iff Equat Appl,(accept)..
尽管对差分方程的研究的结果如此之多,但是,对于周期解的最小周期问题的研究结果相对较少.2004年,庾建设等人首次研究了如下离散单摆方程的上调和解的存在性
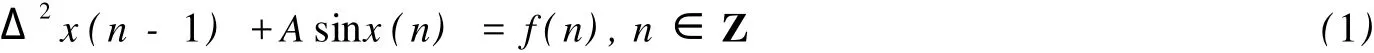
其中,A是一个正常数,f:Z→R是一个T周期函数,Δ是向前差分算子,定义为Δx(n)=x(n+1)-x(n), Δ2x(n)=Δ(Δx(n)),当非线性项是一个奇函数,他们得到次调和解存在性的一个充分条件[12].最近,龙玉华应用Clark定理研究了二阶离散Hamilton系统次调和解存在性.通过运用扰动技巧和对偶最小作用原理,她获得了次二次Hamilton系统次调和解存在性的一些充分条件.
另一方面,在研究微分方程的次调和解的过程中,庾建设引入了一种分解技巧.通过估计周期解对应的泛函的能量值的方法,给出了周期解对应的最小周期估计,从而得到指定周期的次调和解的存在性的一些充分条件.本文的目的是利用这种技巧来得出如下二阶离散Hamilton系统的指定周期的次调和解存在性的一些充分条件

其中,x=(x1,x2,…,xm)′∈Rm,F∈C1(Z×Rm,R),Fx(n,x)=(∂F/∂x1,∂F/∂x2,…∂F/∂xm)∈C(Z×Rm, Rm).把这些条件应用到离散单摆方程中,改进了文献[3]关于次调和解的存性的结果.
1 主要结果
记E∶={x|x=(…,x(-n),…,x(0),x(1),…,x(n),…),x(n)∈Rm,n∈Z}={x(n)}∞n=-∞.对于x,y∈E,a,b∈R,定义
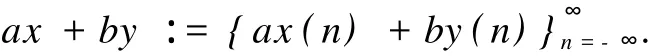
则E是一个向量空间.
给定正整数p,T,定义E的子空间EpT如下
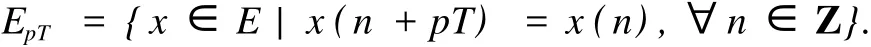
EpT上的范数‖·‖和内积(·,·)定义如下:
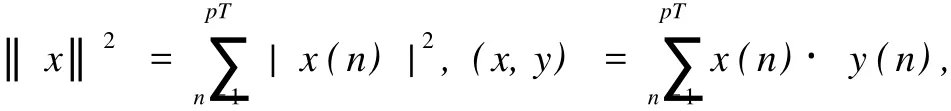
其中,|·|和·为欧氏空间的标准范数和内积.
定义一个线性算子ψ:EpT→RmpT
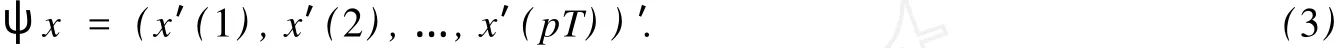
由(3)定义的ψ是一个线性同构,且‖x‖=|ψx|.因此(EpT,(·,·))是一个Hilbert空间,它同构于欧氏空间RmpT.
定义sp为p的最小因子,ω=2π/T,Z[1,m]={1,2,…,m}.假设
(A1)F(n,x)∈C1(Z×Rm,R)是一个偶函数,且关于n是T周期,即对任意n∈Z,x∈EpT,F(-n,-x) =f(n,x),F(n+T,x)=F(n,x).
(A2)存在常数A>0,β>0满足


(A4)如果x=x(n)是一个最小周期为qT的周期函数,其中q是有理数,而且Fx(n,x)是一个最小周期是qT的函数,则q必是一个整数.
定理1.1 令F满足(A1)-(A4).对任意整数p>1,如果还有如下两个不等成立
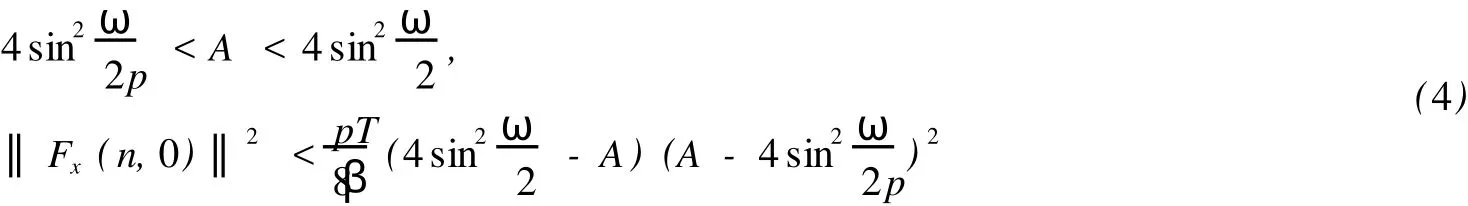
(A3)存在某个常数h∈[0,2sin2(ω βp/2p))满足
则系统(2)至少有一个以pT为最小周期的周期解.
为了证明定理1.1,我们考虑定义在EpT的如下泛函

类似于参考文献[5],(2)的周期解的存在性等价于变分泛函J的临界点的存在性,由于空间EpT与空间RmpT同构的,于是泛函J(x)可以改写为
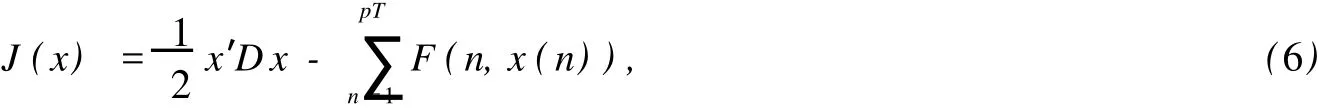
其中x∈EpT,x=(x′(1),x′(2),…,x′(pT))′,矩阵D由参考文献[6]中所定义.直接计算,矩阵D的特征值为λk=4sin2(kπ/pT),k=0,1,2,…,pT-1.于是矩阵D有pT个m重特征值λ0,λ1,λ2,…,λpT-1
对任意1≤i≤[(pT-1)/2],定义
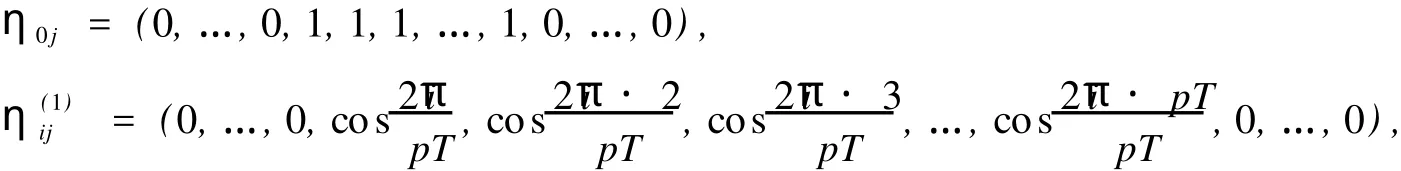
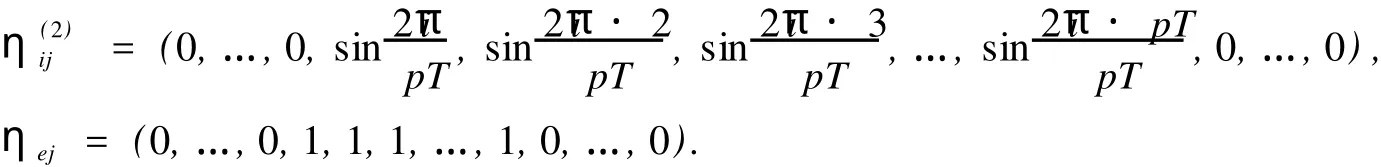
I 当pT是偶数时,
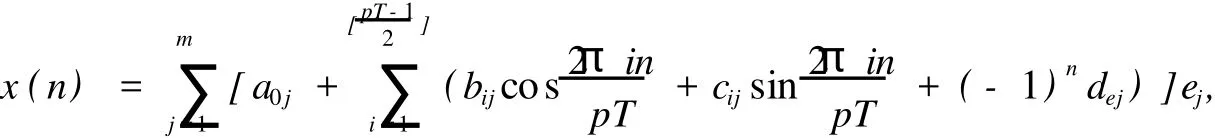
II 当pT是奇数时,
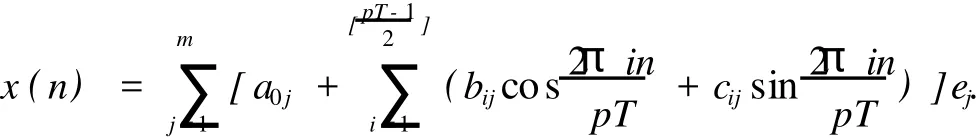
定义EpT子空间~EpT如下:
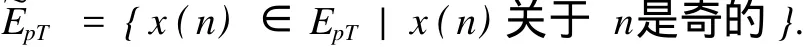
引理1.1 如果x是泛函J在~EpT上的临界点,则x是泛函J在EpT上的临界点并且x的最小周期是T的整数倍.
证明 如果x是泛函J在子空间~EpT上的临界点,则
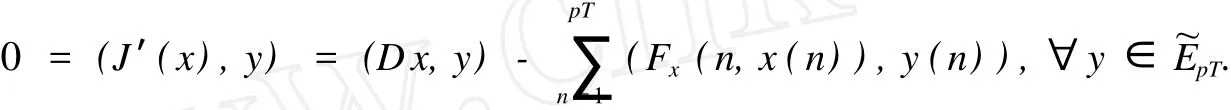
但是对于任意y∈EpT满足y⊥~EpT,有y关于n是偶的,而F(n,x)关于n是偶的,从而Fx(n,x)关于n是奇的,于是可以得到
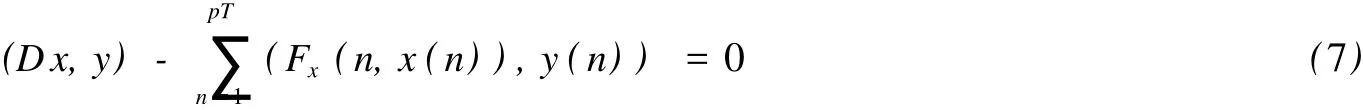
即,对于任意的y∈EpT,有(J′(x),y)=0.这就说明x是J在空间EpT上的临界点.
如果存在某个整数q,使得x的最小周期pT/q,由于x满足
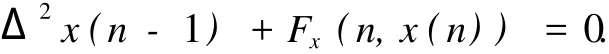
所以,Fx是最小周期也是pT/q.于是假设(A4)隐含p/q必是一个整数.证毕.
引理1.2 J在空间~EpT上有下界并且满足P.S.条件.
证明 由(A3),对于任意,存在一个常数R1>0满足
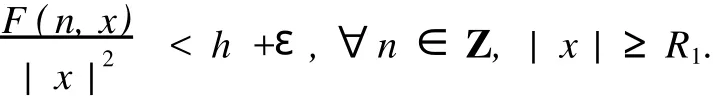
令F1={n|n∈Z[1,PT],|x(n)| 由于F(n,x)是连续,所以∑n∈F1F(n,x(n))有界,于是存在正常数M1满足 当‖x‖→∞时, 所以,J(x)有下界并且任意的P.S.序列有界.因为~EpT是一个有限维空间,P.S.序列必存在一个收敛子列.证毕. 由上面的讨论得J在空间~EpT达到其极小值,记极小值点为x0. 定理1.1的证明 我们只需要证明x0的最小周期是pT.假设存在某个正整数q>1使得x0的最小周期 是pT/q,则x的表达式具有如下形式 定义x1(n),x2(n)如下 则x1是T周期的,并且x1⊥x2,因为Fx(n,0)关于n是T周期的,因此x1⊥Fx(n,0). 根据假设(A2)有 选取¯x(n)=δsin(ωn/p)e1,则直接计算得到 显然,Fx(n,0)是T周期的,于是 如果存在正数δ满足 则J(¯x)≤J(x0),如果J(¯x)=J(x0)则¯x为泛函J在EpT上的一个临界点,它具有最小周期pT,这样我们就证明了定理.如果J(¯x)≤J(x0),这与x0是J在子空间~EpT上的最小值矛盾. 为了证明(9),令δ=h‖x1‖,则 由假设(4) 上式变形就是(11),因此定理结论成立.证毕. 定理1.2 假设F满足(A1),(A3),(A4)以及 (A5)存在常数B>0,A>~A>0满足 对任意整数p>1,进一步假设 并且则系统(2)至少存在一个以pT为最小周期的周期解. 证明 类似于定理1.1的证明,我们只需要证明x0的最小周期是pT. 取 我们有 于是 由x0的定义,我们有J(x0)≤J(¯x),如果J(x0)=J(¯x),则x0是泛函J在空间~EpT上的一个临界点,它的最小周期是pT,这就完成了定理的证明.如果J(x0) (14)隐含 这与假设(12)矛盾.证毕. 文献[12]中,庾建设等给出了如下的结果 定理2.3 假设: (F1)函数f:Z→R是最小周期为T的T周期的奇函数.则方程(1)至少有一个奇T周期解.更加一步,如果存在某个整数p>1, (F2) (F3)其中,¯δ是方程sinδ=(ω2/Ap2)δ在区间(0,π)的解,¯f=(f(1),f(2),…,f(pT))T.则方程(1)至少有一个以pT为最小周期的周期解. 应用定理1.1到离散单摆方程,我们得到以下结果: 定理2.4 假设f(n)是一个以T为最小周期的周期函数.如果存在常数A使得则方程(1)至少存在一个以pT为最小周期的周期解. 证明 我们取F(n,x)=A(1-cosx)-f(n)x,则Fx(n,0)=f(n)并且在(4)中,令β=,有这就是假设(15).因此定理1.1假设成立.应用定理1.1,就证明了这个定理.证毕. 在定理2.3中的条件(F3),作者用无理函数来作为条件给出单摆方程次调和解的存在性.由于无理方程在处理的时候比较麻烦,因此,在实际应用过程中很难验证,而在定理2.4,我们去掉了无理方程,用不等式给出单摆方程次调和解的存在性,因此,在实际应用中,我们的条件要好验证些. 推论2.1 假设f(n)是以T为最小周期的周期的函数.如果存在常数A满足 则存在一个P>0满足,对于任意素数p>P,(1)至少存在一个以pT为最小周期的周期解. 证明 令p→∞,(13)约化成为‖f‖2≤3pπA/(ω)(4sin2-A),这就是假设(16),应用定理2.4就证明了这个定理. [1] BOHNER M.Linear Hamiltonian Difference Systems:Disconjugacy and Jacobi-type Conditions[J].J M ath AnalAppl,1996:804-826. [2] CHEN P,FANG H.Existence of Periodic and Subharmonic Solution for Second-order P-LaplacianDifference Equations[J].Adva D iff Equa,2007,2007:9. [3] CHEN S Z.Disconjugacy,Disfocality,and Oscillation of Second Order Difference Equations[J].J D iff Equat,1994,107:383-394. [4] DENG X Q,CHENG G.HomoclinicOrbits for SecondOrderDiscrete Hamiltonian Systemswith PotentialChanging Sign[J].Acta ApplM ath,2008,103:301-314. [5] GUO ZM,YU J S.Existence of Periodic and Subhar monic Solutions for Second-order Superlinear Difference Equations[J].Sci China(SerA),2003,46:506-515. [6] GUO ZM,YU J S.The Existence of Periodic and Subharmonic Solutions for Solutions of Subquadratic Second OrderDifference Equations[J].J London M ath Soc,2003,68:419-430. [7] LONG Y H.Applicationsof ClarkDuality to Periodic SolutionswithMinimal Period forDiscrete Hamiltonian Systems[J].J M athAnalAppl,2008,342:726-741. [8] MA M J,GUO ZM.HomoclinicOrbits for SecondOrder Self-adjointDfference Equations[H].J M ath AnalAppl,2006,323:513-521. [9] XUE Y F,TANG CL.Existence of a Periodic Solution for Subquadratic Second-orderDiscrete Hamiltonian System[J].Nonlinear Anal,2007,67:2072-2080. [10] YU J S.Subhar monic Solutions with Prescribed Mini mal Period of a Class of Nonautonomous Hamiltonian Systems[J].J Dyn D iff Equat,2008,20:787-796. [11] YU J S,GUO ZM.BoundaryValue Problems of Discrete Generalized Emden-Foeler Equation[J].Sci China SerA,2006,49: 1303-1314. [12] YU J S,LONG Y H,GUO ZM.Subharmonic Solutionswith PrescribedMini mal Period of a Class of a Discrete Forced Pendulum Equation[J].J Dyna D iff Equat,2004,16:575-586. [13] YU J S,SH I H P,GUO ZM.Homoclinic Orbits for Nonlinear Difference Equations Containing Both Advance and Retaration [J].J M ath Anal Appl,2009,352:799-806. [14] YU J S,ZHU B S,GUO ZM.Positive Solutions forMultiparameter Semipositone Discrete BoundaryValue ProblemsVia VariationalMethod[J].Adv D ifference Equ,2008,2008:15. Subharmon ic Solutions with PrescribedM in i mal Period of a Class of D iscrete Ham ilton ian System s XI AO Hua-feng By using a decomposition technique to estimate the energy of a solution in ter ms of the minimal period of the solution,we obtain some sufficient conditions for the existence of subhar monic solutionswith prescribed minimal period of discrete Hamiltonian systems.When the results are applied to the discrete pendulum equation,some sufficient conditions,which are simpler to verify than those in the literature,for the existence of subharmonic solutions are obtained. critical point;subhar monic solutions;prescribed minimal period;discrete Hamiltonian systems O175.7 A 0253-2395(2010)04-0486-07 2009-10-19; 2010-01-04 国家自然科学基金(10871053);博士点基金(20061078002) 肖华峰(1980-),男,湖南衡阳人,博士,研究领域:差分方程、时滞方程,E-mail:hnhyxhf@yahoo.com.cn 文章编号:0253-2395(2010)04-0513-06
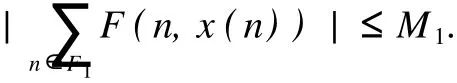
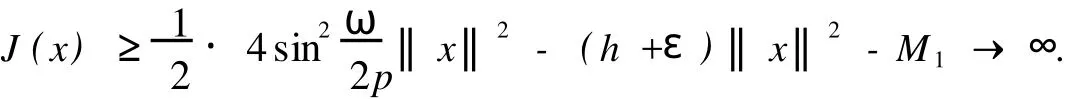
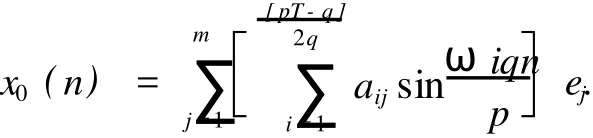

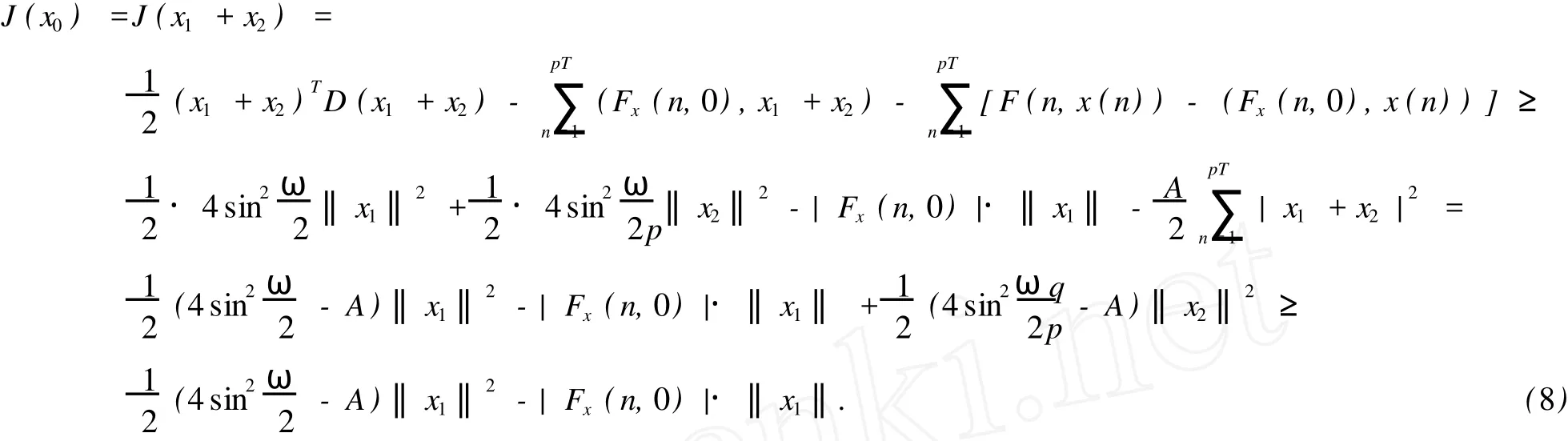


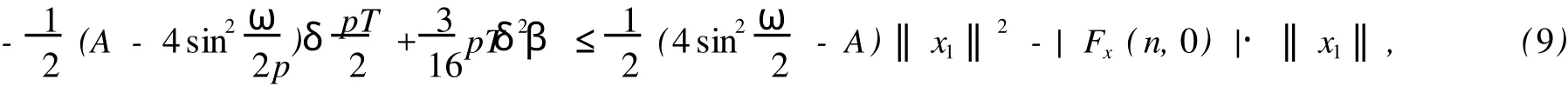


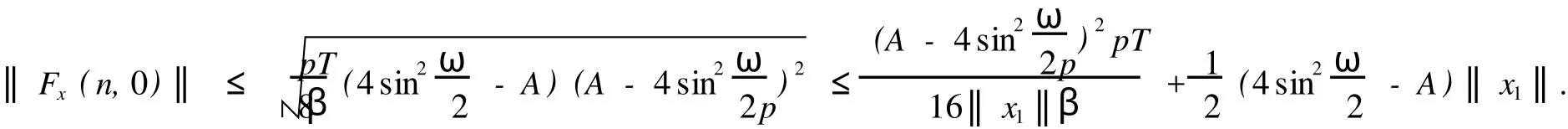
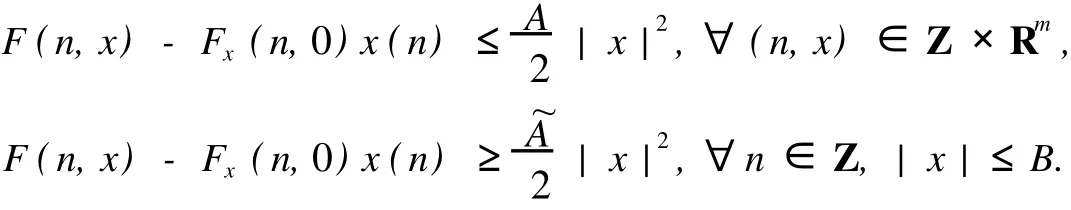
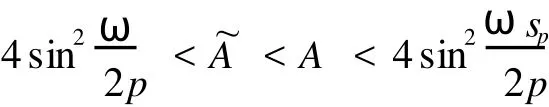
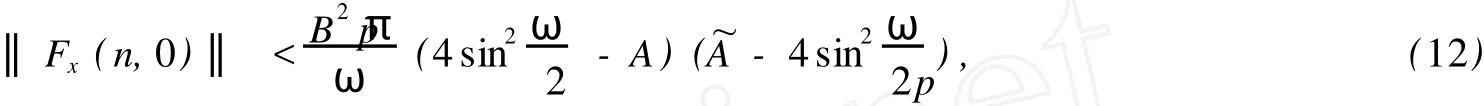

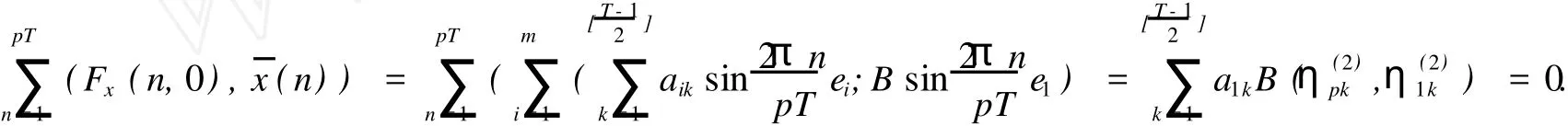
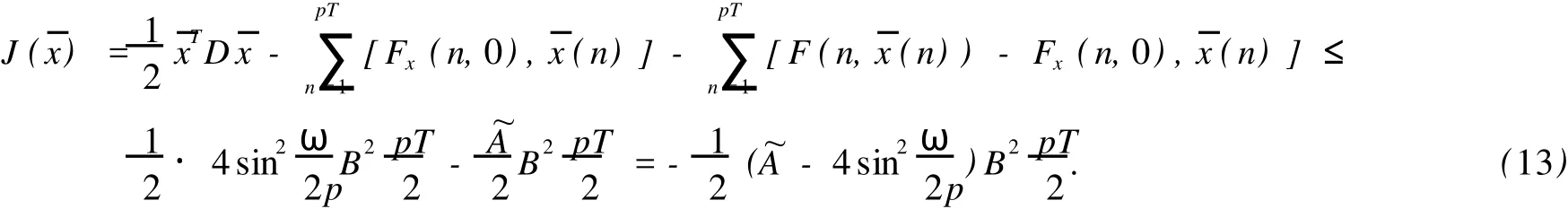

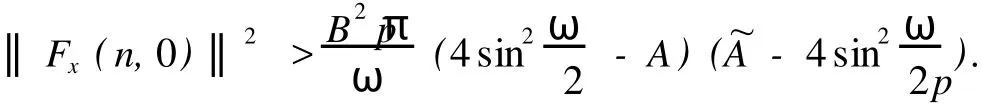
2 应用到单摆方程
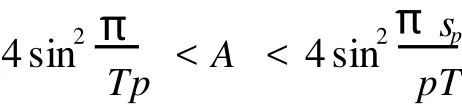

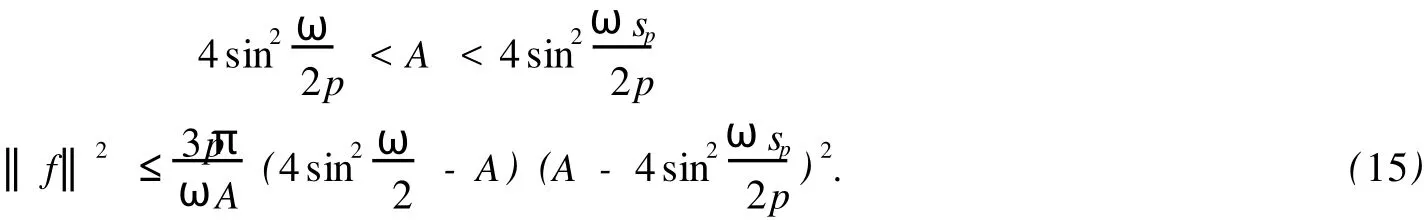
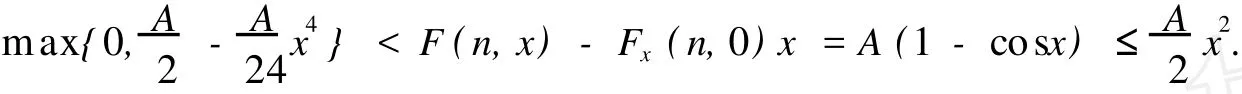
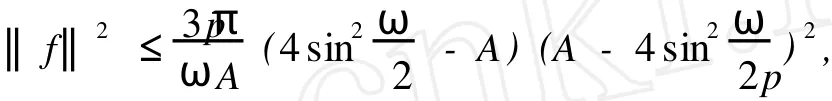

(College of M athem atics and Infor mation Sciences,Guangzhou University,Guangzhou510006,China)

