p2q阶群的完全分类
陈松良
p2q阶群的完全分类
陈松良
(贵州师范学院数学与计算机科学学院,贵州贵阳550018)
设p,q为奇素数,且p>q.文章对p2q阶群进行了完全分类并获得了其全部构造:当q/|p2-1时,恰有2个彼此不同构的类型;当q|p-1时,恰有个彼此不同构的类型;当q|p+1时,恰有3个彼此不同构的类型.
有限群;同构分类;群的表示
设p,q是奇素数,p>q.文献[1](例4.5.1)研究了pq2阶群,得到了其全部构造.本文将研究p2q阶群,并决定p2q阶群的全部构造.
设G是p2q阶群,P是G的一个Sylowp-子群,Q是G的一个Sylowq-子群.由于p>q,所以由Syolw定理(文[2]之定理7.1)得P◁G,从而G=PQ.显然,P或为p2阶循环群,或为p2阶初等交换群,因此可以作如下讨论.
1 P是循环群
这时,可设G=〈a,b〉,而ap2=1=bq,b-1ab=ar,且rq≡1(modp2).显然,P=〈a〉的自同构群Aut(P)是p(p-1)阶循环群,所以b诱导的P的自同构的阶为d=(q,p(p-1)).于是当q|/p-1时,必有d=1,即b诱导的P的自同构只能是恒等自同构,从而G是交换群,因此G必是p2q阶循环群,即
G=〈a|ap2q=1〉.(1)
当q|p-1时,则d=1或q,如果d=1,那么G的构造如(1).如果d=q,那么G不是交换群.这时,由文[3]之定理3.7,可设α是模p与p2的一个公共原根,则由[a,bq]=1可知r是ri=α,i=1,2,…,q-1,之一.取r=r1=α,则得G之一构造如下:

假若取r=ri,1 然而,(2)与(3)是同构的.事实上,如果在(2)中令b1=bi,那么G=〈a,b〉=〈a,b1|ap2=1=bq1,b-1 1ab1= ari〉.因此当q|p-1时,G除为循环群外,还恰有一个非交换群,且其构造同构于(2). 这时,可设P=〈a,b|ap=bp=1=[a,b]〉,Q=〈c〉,于是P的自同构群Aut(P)的阶是(p2-1)(p2-p).当q|/p2-1时,则Q诱导的P的自同构只能是恒等自同构,从而G是交换群,其构造如下: 当q|p2-1时,Q除了诱导P的恒等自同构外,还可能诱导P的一个q阶自同构,因此这时G除了是交换群之外,也可以是非交换群.我们可分为下面两种情况进行讨论. 2.1 群G是超可解群 这时,群G必有一个p阶正规子群,不妨设〈b〉◁G.从而〈b〉Q是pq阶群,于是当q|p-1时,由[2]之命题7.3得 其中α为模p的一个原根. 因为c互素作用在P上,所以据文[4]之定理8.4.6,不妨设〈a〉也是G的正规子群.于是可设c-1ac= as,从而sq≡1(modp),故必有s≡rimodp,i=0,1,2,…,q-1. 由于已假定G是非交换群,所以CP(c)≠P,当CP(c)是p阶群时,不妨设CP(c)=〈a〉,于是s≡1(mod p).因此得G的构造是: 如果CP(c)=1,则r与s模p都不同余于1,不妨设r≡(modp)(否则可用c的适当方幂代替c),于是必有s≡rimodp,i=1,2,…,q-1令 易见(6)与(7)中的每一个都是不同构的.在[7]中若Gi≅Gj,i,j∈{2,3,…,q-1},i≠j,则存在k∈{1,2,…, q-1}及正整数m,n,s,t使得 并且在Gi中当由此得 当k≠1时,由(12)得t≡0(modp),再由(8)得s≢0(modp),由此及(11)又得 由(13)及(9)得m≡0(modp),再由(8)得n≢0(modp),从而由(10)得k≡j(modq).由此及(13)得 当k=1时,类似上面的讨论,可得i=j.反之,若(14)成立,则Gi≅Gj.因此 2.2 群G不是超可解群 这时,P必是G的极小正规子群,从而Q是G的极大子群,且NG(Q)=Q.于是由[5]之定理V.7.6,知G是补为Q而核为P的Frobenius群,所以q|p2-1. 因为Q=〈c〉,所以c可以看成p元域Fp上的2阶矩阵.显然c在P上的作用是不可约的,所以c没有1维不变子空间,于是c的特征多项式f(λ)是p元域Fp上的2次不可约多项式.又因为λq-1是c的零化多项式,所以f(λ)是λq-1的因式.众所周知,λp2-λ是Fp上的所有一次不可约多项式和二次不可约多项式的积,于是f(λ)也是λp2-1-1的因式,但在Fp上λp-1-1=(λ-1)(λ-2)…(λ-(p-1)),所以f(λ)不是λp-1-1的因式,因而(q,p-1)=1,从而必有q|p+1.反之,若q|p+1,则(λq-1,λp-1-1)=λ-1,从而(λq-1)/(λ-1)是(q-1)/2个互不相同的2次不可约多项式的积.用|c|表示矩阵c的行列式,则由于cq=1, 总而言之,当q|p-1时,如果G是非交换的有初等交换Sylowp-子群的p2q阶超可解群,那么它恰有可以知|c|q≡1(modp).又|c|p-1≡1(modp),且q与p-1互素,可知|c|≡1(modp),从而可设c的特征多项式为f(λ)=λ2-β λ+1.因此,可得G的构造为: 显然,对任何不被q整除的正整数k,ck都是Q的生成元(共q-1个),而且ck的特征多项式(记为fk(λ))都是2次不可约多项式,且当i≠j时fi(λ)=fj(λ)的充要条件是ci与cj相似,亦即pi≡j(modq).因对任何固定的i,恰有一个j≠i,使得pi≡j(modq),从而推知fi(λ),1≤i≤q-1,中恰有(q-1)/2个互不相同的,所以当f(λ)是整除λq-1的任一个不可约多项式时,按上述方法得到的G的构造必与(15)同构. (i)当q/|p2-1时,G恰有2个彼此不同构的类型,其构造分别是:(1),(4); (iii)当q|p+1时,G恰有3个彼此不同构的类型,其构造分别是:(1),(4),(15). 当q=3时,定理1显然有下面的推论. 推论1(文[1]之例4.5.2) 设p为奇素数,且p>3,而G是3p2阶群.则当3|/p-1时,G恰有3个彼此不同构的类型;而当3|p-1时,G恰有6个彼此不同构的类型. 综上所述,我们得到下面的定理: 定理1 设p,q为奇素数,且p>q,而G是p2q阶群.则: [1] 张远达.有限群构造[M].北京:科学出版社,1982. [2] AKOERUB J L,BELL R B.Groups and Representation[M].Beijing:World Publishing Corporation,1997. [3] NATHANSON M B.ElementaryMethods in Number Theory[M].Beijing:World Publishing Corporation,2003. [4] KURZ WEI L H,STELLMACHER B.The Theory of Finite Groups[M].New York:Springer-Verlag,2004. [5] HUPPERTB.Endliche Gruppen I[M].Berlin:Springer-Verlag,1967. On the Classification of Fin ite Groups of Orderp2q CHEN Song-liang Letp,qbe odd primes such thatp>q,andGbe a finite group of orderp2q.It is discussed that the isomorphic classification ofG,and their presentations are completely described.The results showed that:Ifq|/p2-1,G had 2 nonisomorphic presentations;Ifq|p-1,Ghadnonisomorphic presentations;Ifq|p+1,Ghad 3 nonisomorphic presentations. finite group;isomorphic classification;presentation of group O152.1 A 0253-2395(2010)04-0493-03 2010-01-19; 2010-05-23 贵州师范学院自然科学研究资助项目 陈松良(1964-),男,湖南双峰人,博士,副教授,从事代数学及其应用研究.E-mail:chsl2006@yahoo.com.cn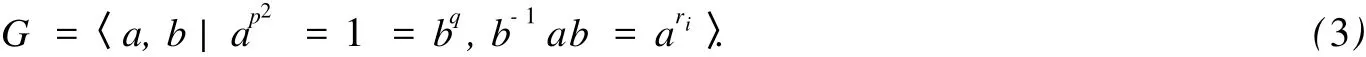
2 P是初等交换群
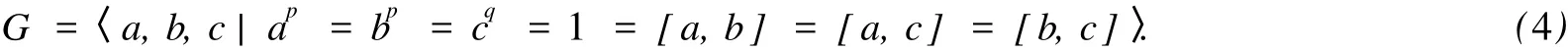







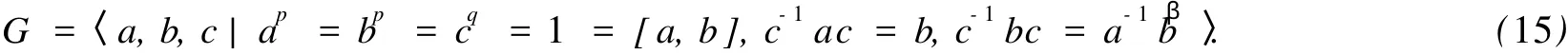
3 结论
(School of M athem atics and Computer Science,Guizhou Nor m al College,Guiyang550018,China)

