判断一类双系统同时精确可观测的充分条件

杨 威,李胜家

判断一类双系统同时精确可观测的充分条件

杨 威,李胜家

(山西大学数学科学学院,山西太原030006)

利用反自伴算子生成系统是精确可观测的Hautus条件,得到判断如下双系统同时精确可观测的充分条件.

线性系统;Hautus条件;同时精确可观测性

弹性系统的振动控制和边界控制是数学工作者和工程人员们一直以来所关心的一种重要的分布参数系统问题.近些年来,人们对于弹性系统的边界控制进行了广泛的研究,在分布参数边界控制系统的精确可控性、可观测性、稳定性和最优控制的研究中得取了一些很好的结果,见文献[1-3].此外,在分布参数系统已得结论的基础上,许多学者开始寻找双系统乃至多系统同时可控和同时可观测的判断条件.本文考虑如下两个无穷维抽象线性系统(A1,C1)和(A2,C2)的同时精确可观测性,其状态分别用z1和z2表示:

其中,“·”表示对时间t的微分,A1和A2分别是相应状态空间上强连续算子半群的生成元,C1和C2为相容性观测算子.

同时精确可控性和可观测性首先是由Russell在文[4]中所提出的,它也是Lions在文[5]第六章所研究的内容.该问题主要讨论如何判断无穷维双系统是同时精确可控和同时精确可观测的.但是到目前为止还没有一个能够从本质上判断无穷维双系统是同时精确可控和同时精确可观测的充要条件,它仍然是一个公开问题.许多学者都对该问题进行了深入的研究,并且得到了一些比较好的结果,见文献[6-8].本文利用反自伴算子生成系统是精确可观测的Hautus条件,得到了判断上述双系统同时精确可观测的充分条件.

1 主要定理及其应用

假设X是Hilbert空间,算子A是空间X上强连续半群(T(t))t≥0的无穷小生成元.定义Hilbert空间X1=(D(A),‖·‖1),其中‖z‖1=‖(βI-A)z‖,β∈ρ(A)固定.在文[9]中,关于无穷维空间上反自伴算子生成系统是精确可观测的Hautus条件为:设反自伴算子A在Hilbert空间X上生成C0-半群(T(t))t≥0, Y是Hilbert空间且算子C∈L(X1,Y)是对于半群(T(t))t≥0的相容性观测算子,那么系统(A,C)是精确可观测的当且仅当存在正常数M,m使得:

定理1 对于j∈{1,2},设反自伴算子Aj是Hilbert空间Xj上强连续半群(Tj(t))t≥0的无穷小生成元,Y是Hilbert空间且Cj∈L(Xj1,Y)是对于半群Tj的相容性观测算子.设系统(A1,C1)和(A2,C2)都是精确可观测的,如果系统还满足对于任意的z1∈D(A1),z2∈D(A2),函数

在x=0处有φ′(0)≥0,那么一定存在时刻T0>0,使得双系统(A1,C1)和(A2,C2)在任何时刻T>T0是同时精确可观测的.

证明:由于系统(A1,C1)和(A2,C2)都是精确可观测的,故存在Mi,mi>0(i=1,2),满足:

定义:

为了说明双系统(A1,C1)和(A2,C2)的同时精确可观测性,只需证明系统(A,C)是精确可观测的.利用(1), (2)两式:对于任意的Φ∈H1(R),z1∈D(A1),z2∈D(A2),有:

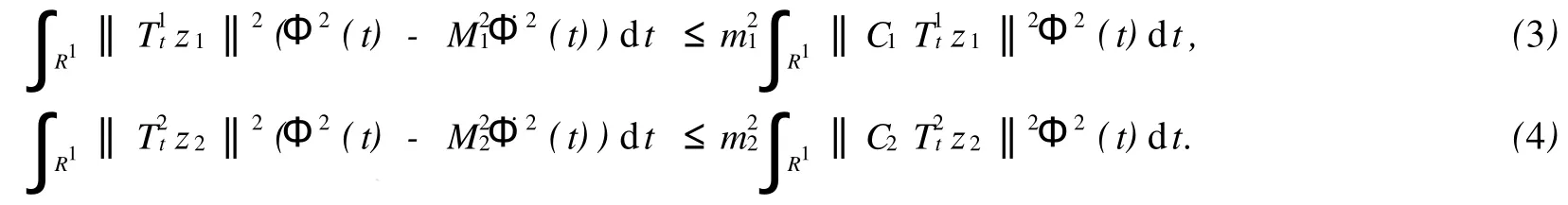
即:

事实上,取M2=M21+M22,m2=2(m21+m22),并且利用(3),(4)式有:

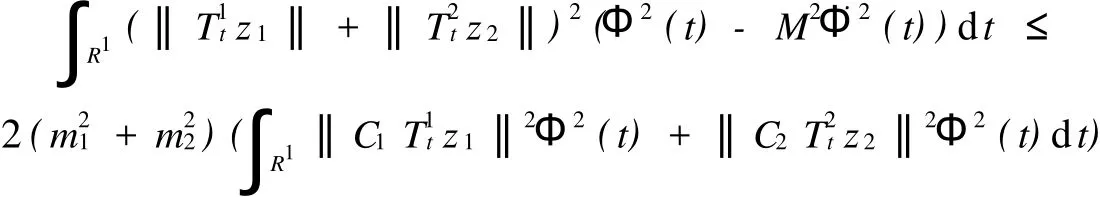
由于对于任意的z1∈D(A1),z2∈D(A2),函数φ(x)=‖C1T1tz1+xC2T2tz2‖2在x=0处有φ′(0)≥0.所以有

即:对于任意的Φ∈H1(R),z1∈D(A1),z2∈D(A2),存在正常数M,m使(6)式成立.

下面给出(6)式左端的一个下界,由于算子A1,A2均是反自伴算子,故算子仍然为一个反自伴算子,故半群是一个酉群,因此:

其中

对ψ≠0且τ充分大时,就有Iτ(ψ)>0.因此,便得双系统(A1,C1)和(A2,C2)同时精确可观测不等式:

如果选取:

则当τ>Mπ时,Iτ(ψ)>0,故系统(A1,C1)和(A2,C2)在时刻T>T0=Mπ是同时精确可观测的.

例1 考虑长度为π的弹性弦波动方程:定义状态空间为X=H10(0,π)∩L2[0,π],在下述内积的定义下,该空间为一个Hilbert空间:定义算子A:D(A)→X为:其中D(A)=[H2(0,π)∩H10(0,π)]×H10(0,π).用Z＊表示非零整数,那么对于任意的n∈Z＊,记φn(x)=sin(nx).容易验证下面一组向量(Φn)n∈Z＊:

为算子A的相应于特征值λn=in,n∈Z＊的特征向量,并且构成空间X的一组标准正交基.同时,算子A还生成空间X上的等距半群T(t):

其中,ψn(x)=cos(nx),∀n∈Z＊.利用指数族{eint}n∈Z＊在L2[0,2π]中的正交性,可知:

因为φ-n=-φn且ψ-n=ψn,故有:

再利用(ψn)n≥0和(φn)n≥0在L2[0,π]中的正交性,有:

因此,可知算子C是相容性观测算子且系统(9)在时刻T≥2π是精确可观测的.同样的方法,还是考虑系统(9),但此时选用的观测算子为:

所以,仍然有算子～C是相容性观测算子且系统(A,～C)在时刻T≥2π是精确可观测的.

利用定理1可知:系统(A,C)和(A,～C)在T>2π的某个时刻以后是同时精确可观测的.

[1] KOMORNIK V.Exact Controllability and Stabilization-The Multiplier Method[M].RAM Res Appl Math,John Wiley Chichester U K Masson Paris,1994.

[2] YAO Peng-fei.On the Observability Inequalities for Exact Controllabiltiy of Wave Equations with Variable Coefficients [J].S IA M J Control Optim,1999,37:1568-1599.

[3] CHAI Shu-gen,LIU Kang-sheng.Observability Inequalities for the Transmission of Shallow Shells[J].S ystems Control Letters,2006,55:726-735.

[4] RUSSEL D L.The Dirichlet-Neumann Boundary Control Problem Associated with Maxwell’s Equations in a Cylindrical Region[J].S IA M J Control Optim,1986,24:199-229.

[5] LIONS J L.Exact Controllability,Stabiliztion and Perturbations for Distributed Systems[J].S IA M Review,1988,30:1-68.

[6] HANSEN S W,ZHNAGB Y.Boundary Control of a Linear Thermoelastic Beam[J].J Math A nal A ppl,1997,210:182-205.

[7] TUCSNAK M,WEISS G.Simultaneous Exact Controllability and some Applications[J].S IA M J Control Optim,2000, 38:1408-1427.

[8] AVDONIN S A,WILLAM.Simultaneous Control Problems for Systems of Elastic Strings and Beams[J].S ystems Control Letters,2001,44:147-155.

[9] RAMDANI K,TAKAHASHI T,TENENBAUM G,et al.A Spectral Approach for the Exact Observability of Infinite-dimensional Systems with Skew-adjoint Generator[J].J ournal of Functional A nalysis,2005,226:193-299.

Sufficient Conditions for Judging Simultaneous Exact Observability of a Class of Two Systems

YANG Wei,LI Sheng-jia
(School of Mathematical Science,S hanxi University,Taiyuan030006,China)

By using of Hautus conditons for exact observability with a skew-adjoint generator,we obtain the sufficient conditons for simultaneous exact observability of the following two systems.

linear system;Hautus conditions;simultaneous exact observability

O177

A

0253-2395(2010)02-0169-04

2009-04-08

山西省自然科学基金(2007011002)

杨 威(1982-),男,山西大同人,助教,主要从事分布参数控制系统研究.E-mail:yangwei@sxu.edu.cn

文章编号:0253-2395(2010)02-0238-06