“数形结合”在物理教学中的应用

◆何 涛

(甘肃省秦安县第一中学)

“数形结合”在物理教学中的应用

◆何 涛

(甘肃省秦安县第一中学)

所谓“形”就是用图形来表示物理状态与物理过程,“数”就是物理量,“数形结合”就是在物理模型的图形上标出已知量和未知量。特别是对多过程问题,由于过程复杂,物理量又多,采用“数形结合标点标量”,能使物理过程非常清晰,使已知量和未知量非常明确,使物体的受力和运动的关系非常明朗,从而简单地寻找出物理规律和公式,解决实际问题。

“数形结合”物理教学 应用

所谓“形”就是用图形来表示物理状态与物理过程,“数”就是物理量,“数形结合”就是在物理模型的图形上标出已知量和未知量。特别是对多过程问题,由于过程复杂,物理量又多,采用“数形结合标点标量”,能使物理过程非常清晰,使已知量和未知量非常明确,使物体的受力和运动的关系非常明朗,从而简单地寻找出物理规律和公式,解决实际问题。

一、高中物理教学中“数形结合”思想方法

新课程实施的基本思路是“重过程”,分析过程就建立物理模型,而这一过程最终落实在图形上,加上物理量,就把物理模型和物理量采用“数形结合”的形式表现出来。

例如,位移 (直线运动最简单的概念之一):是从初位置向末位置做的有向线段 (作出有向线段 a-b、a-c、a-d,并标出 S1、S2、S3就可以直观的说明其大小方向)。在研究位移和时间、速度、时间的关系时,课本上是以图表形式出现,这种图表很难观察到位移和时间、速度和时间的直接关系,当然我们讲课要以“数形结合”的方法。再如,动能定理的推导过程:利用数形结合 (作图、标点、标量)直观的反映状与态的过程,以及状态量和过程量的关系。特别是在动量定理和动量守恒定律的研究中强调方向性,往往会出现因方向混淆的错误。利用数形结合就能很直观的反映出各矢量的大小和方向。这是我们教学中行之有效的方法。

我们教学中不能无物(就是研究对象),研究运动时不能无过程 (就是建立物理模型)。利用数形结合就很好的表现出了这种形式。这样的表示方法更符合实际,学生感到更亲切、思维更活跃、教学效果更明显。

二、数形结合在多过程题型中的应用

在高中阶段的物理学习中,特别是高中一年级的新生,反映比较普遍的问题就是:高中物理难学,课堂上教师讲的内容,基本能听懂,但在处理一些物理问题时感到很茫然,觉得无从下手。究其原因,大多数学生在处理物理问题时,首先是不能建立起相应的物理情景,当然也就谈不上相应的物理模型的建立。即使是有了解题的思路,因为过程不清楚、已知未知量不明确,还是无法寻找出相应的关系,无法选出合理原来和合理的公式。

上课讲题或学生问题时,我的就让他们根据生活经验,先做实验,自己感受实验全过程,自己画出过程图形,并标出已知未知量,这样做后大多数学生都能解决实际问题了。这种作图的过程就是就是建立物理模型,有了模型并且有了清楚的物理量当然问题就容易解决了。在解决有多过程较难的物理习题时,学生头脑中对物理过程的一个清晰的“数形”图景则是解决问题的关键和保证。下面以力学中运动模型的应用为例加以说明。

例:从地面以一定的速度竖直向上抛出一小球,小球从抛出点上升到最高点所用的时间为 t1,从最高点下落到抛出点所用的时间为 t2。若空气的作用不能忽略,则对于 t1和 t2的大小关系,下列判断中正确的是( )

A.=t1=t2B.t1t2D.无法判断 t1和 t2哪个较大。

【思维导图】

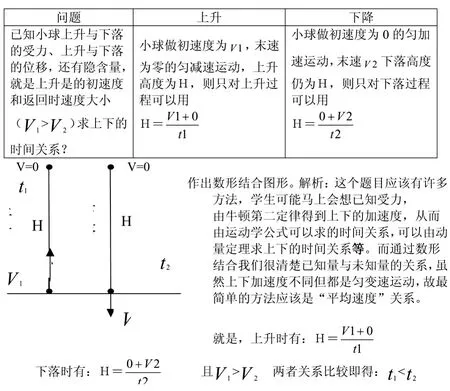
方法讨论:

(1)运动关系的分析中由于涉及的物理量较多,且运动过程复杂,要明确各种关系和运动规律,最合理的方法就是采用“数形结合”。

(2)因为运动学中公式多,过程复杂。有人就问到,为什么要采用平均速度,为什么他自己想不到,究竟解题怎么才能选用简单的方法、合理的公式。我们采用数形结合,这样就会“跳出”你需要的原理和最简单的公式。

(3)我们分析题目通常“数形结合”标点标量。这样做后,不仅明确物理过程、物理量以及物理量之间的关系,同时又设出了未知量特别是临界量。这样,我们就可以采用“程序法”从前到后列出方程。而这种方法是我们解决多过程、比较复杂的题目的最好方法。

(4)引导学生合理建立物理模型,作出解题必须的“数形结合”图形。这不仅能够培养学生良好的思维习惯,使其加深对物理概念和规律的理解,提高解题技巧,达到举一反三的效果,而且对于开发学生智力,发展创造性思维,都起到积极的作用。