优化解题策略,凝练思维品质——解题教学中数学思维敏捷性的培养尝试

◆华维林

(甘肃省永登县第二中学)

优化解题策略,凝练思维品质
——解题教学中数学思维敏捷性的培养尝试

◆华维林

(甘肃省永登县第二中学)

通过对思维敏捷性形成的因素分析,探究培养和发展学生优良数学思维的科学途径,在教学过程中,优化解题策略,提升解题效能,凝练思维品质,增强自信,战胜高考。

思维敏捷性 策略 简缩 探究 效能

良好的数学思维品质向来是高考考查的重点,尤其是对数学思维敏捷性的考查,更加体现了高考命题的匠心独用。学生的思维品质的好坏,直接影响学生的高考成绩,从而间接地影响学生个人的发展。因此,我们应该探究学生的数学思维敏捷性的成因,认识其特点,在教学中制定相应的学习策略,提高教学效果。

一、进行陈述性知识的概括和提炼

储备知识,梳理知识,比较、归纳和总结知识之间的区别与联系,形成知识网络,优化认知结构,以便在解题时有效地激活知识、准确地提取知识、同时扩展思维活动区域,增大思维运动量,减少烦琐的计算,快速地解决问题。

例 1.正方形 ABCD-A′B′C′D′的棱长为α,求异面直线 BD与 B′C的距离。

分析:将异面直线 BD与 B′C的距离转化为两平行平面 A′DC和 B′D′C之间的距离,易知其距离为。其知识储备应是“线线平行、面面平行”等相关定理以及正方体的相关性质。如果采用向量坐标法,就会增大运算量,而且容易出错。事实上,深厚的陈述性知识是知识和能力发生迁移的基础。

二、进行程序性知识的提炼和概括

主要以数学思想为指导,在掌握好通性和通法 (如配方法、待定系数法、换元法、坐标法等)的基础上,通过各种解题方法的比较,进行解题方法的提炼,优化解题策略,提高解题的效能。

1.以数形结合思想为指导,提炼特殊法为数形结合法

2.以特殊与一般思想为指导,提炼特殊法为检验法和排除法

从题干或选择支出发,(通过选取特殊值代入、将问题特殊化或构造满足题设条件的特殊函数或图形特殊位置,)利用问题在某一特殊情况下不真,则它在一般情况下不真这一原理,达到肯定一支或否定三支 (去谬)的方法,称为特殊法。

例 3.(排除法)一个等差数列的前 n项和为 48,前 2n项和为 60,则它的前 3n项和为 ( )

解 结论中不含 n,故本题结论的正确性与 n取值无关,可对 n取特殊值,如 n=1,此时 a1=48,a2=S2-S1=12,a3=a1+2d= -24,所以前 3n项和为 36,选 D。

评析:解一是顺向推理的方法,而解二是反常规的解法,是逆向思维,突破思维定式,达到了更便捷、更迅速的效果。

3.以有限与无限思想为指导,提炼特殊法为极限法。

例 5.(2005北京):对任意的锐角α,β,下列不等关系中正确的是:

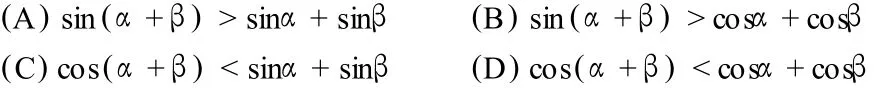
分析:取α与β为 30度、45度、60度等可以排除 A、B,但无法排除 C、D,若进行论证,则更难。若使α趋向于 0,β趋向于 0,则排除A、B、C,选D。

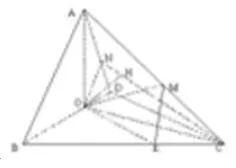
(Ⅰ)求证:面 ABD⊥面 BCD;(Ⅱ)求异面直线 AB与 CD所成的角的大小;

(Ⅲ)求点 E到平面 ACD的距离。

分析:方法一 (几何法):(Ⅰ)由 CA=CB=CD=2知,点 C在面 ABD内的射影为BD的中点O,由线面垂直易得出面面垂直。

(Ⅱ)取 AC的中点M,由平移法知∠OEM为异面直线AB与 CD所成的角,由已知条件易得其大小为

(Ⅲ)因OE平行面ADC,故通过将点面距离转化为线面距离。取AD中点N得ON⊥AD,且 CO⊥面ABD,由三垂线定理易得面ONM⊥面 ADC,过 O作 OH⊥CN于 H,则 OH为点 O到面 ADC的距离,即为点 E到面ADC的距离。或者等积法来求,即VE-ACD=VA-CDE,结果为