将正n边形分成大小形状相同的n等份有无穷多种方法

李海

（和田师专数学系 新疆和田 848000）

将正n边形分成大小形状相同的n等份有无穷多种方法

李海

（和田师专数学系 新疆和田 848000）

我们在中期报告中只是证明了正四边形，在此我们还是用“中点分形法”证明对正n边形命题也成立，又想出了另外的一种证明方法“旋转多边形法”，从而在此基础上推广了一个结论：对一般的图形 P只要具有以下两点性质：1.旋转一个角度θ后与原图形重合；2.存在一个正整数n，使得那么就能将此图形分成大小形状相同的n等份。也可以将其类似等分。

正n边形；分法；等分；无穷

在中期报告中我们证明了正四边形可以分成大小、形状相同的四等份，且有无穷种分法。现我们用“中点分形法”证明对正n边形该结论也成立。

据中期报告的分法可知，取正n边形边的中点，连接这些点，组成的仍为正n边形，找出其中心，连其中心和中点，如图1所示：

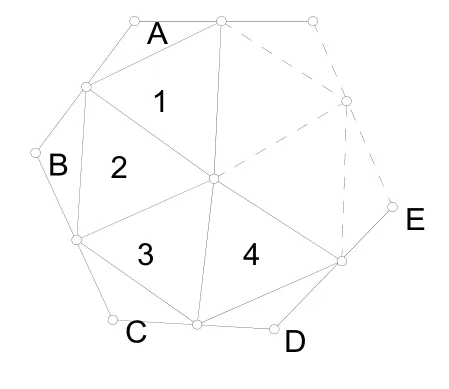
图1

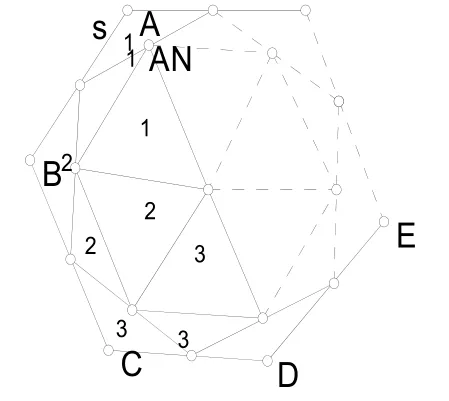
图2

1A，2B，3C，4D都是大小形状相同的，这就是一种分法。更进一步，在刚刚那个正n边形的基础上，可以用同样的办法。如图2所示，就是在刚刚所得正n边形的基础上做得，其中相同数字的块组成一个大块，111，222，333……都是大小形状相同的，故这又是一种分法。如此反复下去，对于正n边形，把它分成大小、形状相同的n等份有无穷种方法。这个方法简单易行，而且还很直观。

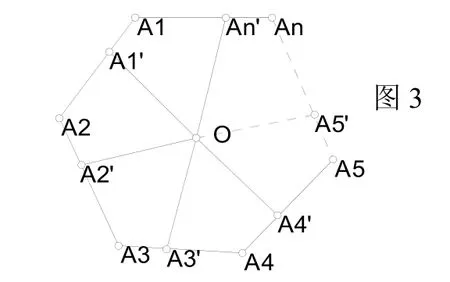
在此基础上，我们又想到另外的一种证明方法“旋转多边形法”：记正n边形的中心为O，分别在边上取使得连接则又因为正n边形绕O旋转与原多边形重合，其中与与与重合，′与′与与重合，即有四边形与四边形重合，…四边形与四边形重合，所以有四边形四边形四边形与四边形大小形状完全相同，而且是对应边上使得成立的任意点，故有无穷多种取法，从而分法有无穷多种，命题得证。

经过上面对正n边形的分法，我们进一步推广证明了对一般的图形P只要具有以下两点性质：

1.旋转一个角度θ后与原图形重合；

由性质1知该图形存在旋转中心，设该图形的旋转中心为O，然后在该图形的任一边（若该图形是由曲线围成，则只须在该曲线上任取一点即可）上选取一点A1，连接旋转中心和该点，将直线OA1按顺时针方向旋转角度θ与该图形交于A2点，将此手续进行n次，分别与该图形交于A3、A4…An点，连接OA2、OA3…OAn，很容易验证这n个图形大小形状相同，由点A1的任意选取性可知该分法有无穷种，证毕。

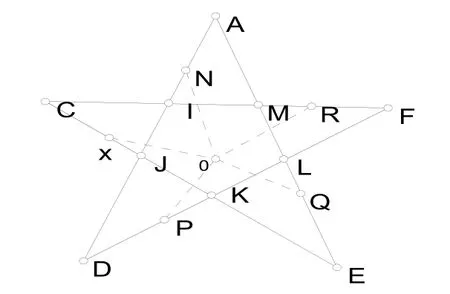
图4

如图4：图形五角星ACDEF，N，X，P，Q，R是在边上取得点，保证NI=XJ=PK=LQ=RM，就可以知道多边形ANORM，CXONI，DPOXJ，EQOPK，FROQL，大小形状都相等，此为一种分法。因为N，X，P，Q，R是在边上任意取得，故有无穷多种分法。

特别的，我们可以猜测在三维空间中，对于正多面体，我相信也可以用我们的分法来将其等分。

以上只是通过几何作图方法简单的证明了推广的结论，由于所学知识有限，对旋转体和图形结构还不能深入研究，因此在这不能从理论上系统证明，因此该证明待续。

经过这一段时间的学习与研究，我们从系统上证明了可将正 n边形等分成大小、形状相同的n等份，且有无穷种分法。我们先从正四边形中着手，由简单到复杂，由具体到抽象，一步一步地完成，得到我们所要证明的结论。然后我们还作了进一步推广，对具有上述性质1和性质2的一般图形P仍然可以等分成大小、形状相同的n等份，且有无穷种分法。

这里，我们只是从几何作图方法简单证明了该结论。不过我们还是希望可以用数学软件把分图的过程表达出来。经过一起讨论思考，我们猜想：对于一般的n维欧氏空间，当它满足一定条件后，仍可以像上述结论一样，可以等分成具有相同性质（大小、形状或者说是基、维数等性质）的n等份，且有无穷种分法，这有待于我们进一步学习与探究。

[1]李尚志，陈发来.数学实验[M].高等教育出版社，1999.

[2]戴一奇，胡冠章，陈卫.图论与代数结论[M].清华大学出版社，1995.

[3]李海.将正四边形分成大小形状相同的四等份有无穷多种方法[J].和田师专学报，2010（1）.

和田师专研究计划基金资助项目《将正N边形分成大小形状相同的N等份有无穷多种方法》部分研究成果，项目编号：1076509073

李海（1985-），男，江西吉安人，和田师专数学系助教，从事数学教育工作与研究。

2010-07-12