足球体的构造和性质

徐兴国

（1.华东师范大学数学系 上海 200000；2.扬州教育学院 江苏扬州 225600）

足球体的构造和性质

徐兴国

（1.华东师范大学数学系 上海 200000；2.扬州教育学院 江苏扬州 225600）

本文从足球体的构造出发，分析讨论了足球体的各种几何性质，如面面角、单位体积、顶点坐标等，并在其基础上，进一步讨论了足球体所对应的足球体群及其性质，最后介绍了它的简单应用。

足球体；构造；几何性质；群

早在千年以前，古希腊人就发现了正多面体。所谓正多面体是指：多面体的各个面都是全等的正多边形，并且各个多面角都是全等的多面角。三维空间中的正多面体有且仅有5种，分别为正四面体、正六面体、正八面体、正十二面体和正二十面体，其构造方法及性质可参考文。[1]半正多面体与正多面体类似，是一类具有高度对称性的几何体，其定义为：使用两种或以上的正多边形为面的凸多面体。它们拥有非常美的几何外形，如图 1。下面介绍的足球体就是其中的一种，因其形如足球，故称为足球体。

图1

1.足球体的构造

足球体是由20个正六边形和12个正五边形拼接而成的，如图1。a.其具体参数如下：

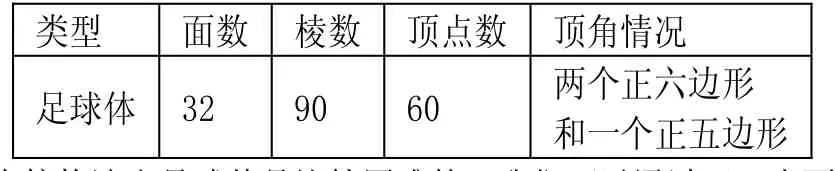
类型 面数 棱数 顶点数 顶角情况足球体 32 90 60 两个正六边形和一个正五边形

直接构造出足球体是比较困难的，我们可以通过正二十面体间接的来构造出足球体，方法如下：取正二十面体每条棱上的三等分点，然后在每个面上将它们连接起来，再截去每个顶点处的正五棱锥，剩下的几何体便是足球体，如图 2。为了行文的方便与统一，这里规定被切割的正二十面体的边长为1。

2.足球体的几何性质

2.1 面面角。足球体的面面角有两种，一种是正六边形与正六边形所成二面角，设为∂；另一种是正六边形与正五边形所成的二面角，设为β。接下来就分别求∂与β的值。

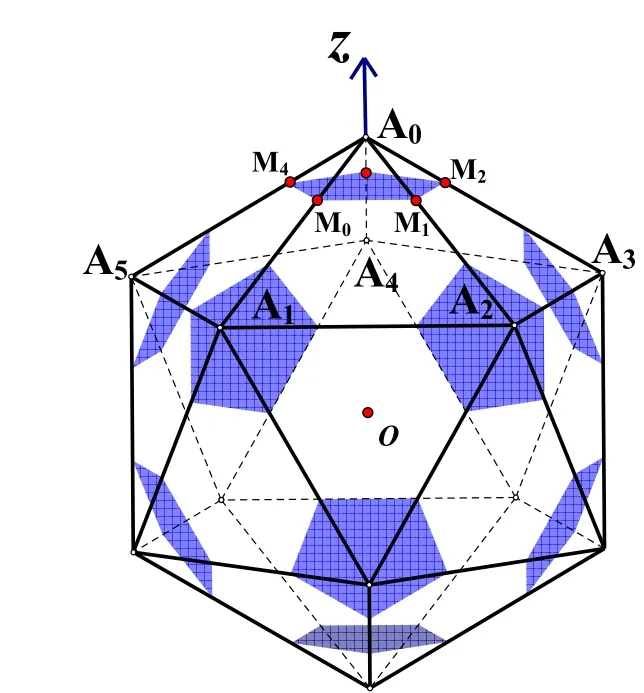
图2

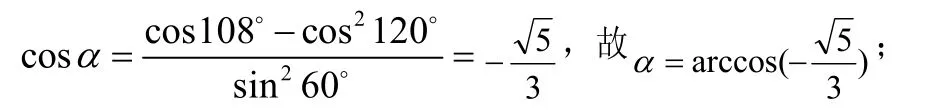
同理可得：

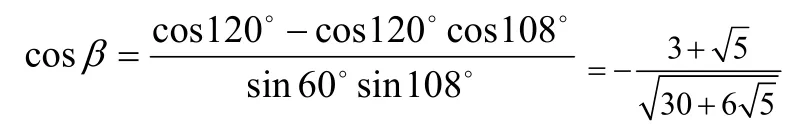
2.2 足球体的体积。将足球体的中心与各顶点连接，就将足球体分割成了12个全等的正五棱锥与20个正全等正六棱锥，易得：

2.3 足球体各顶点的坐标。足球体共有60个顶点，为了求出它们的顶点坐标，先来求一求它的母体——正二十面体的顶点坐标。将正二十面体中心O和原点重合（如图2）一对顶点A0和B0置于z轴上，A0在正 z向，按正 z轴的右手螺旋方向，顺序记作Ai，在xoz平面内的偏正x轴方向，在xoy平面下方的六个顶点分别记为Bi，0≤i≤5，关于原点对称的两个顶点有相同的下标。不难计算出它们的坐标：

坐标A （0，0，5 0 8 5+ ）8 A （1 1 10 + ，0，1(5 5) 8 1+ ）85 A （1 1 1(5 5) 2 10 − ，2 1 1(3 5) 2 2 + ，8 1+ ）85 A （1−+，12 1 3，25 12 8 1+ ）85 A （−+，1+ ）12 1−，1 4 25 12 8 85 A （1 1 1(5 5) 210− ，− +，5 1 1(3 5) 2 2 8 1+ ）85

下面来计算足球体的顶点坐标。由于足球体的顶点都是原二十面体棱的三等分点，设足球体第一层上的顶点按正z轴右手螺旋方向，顺序记为由定比分点的定义可得再由定比分点公式可得：

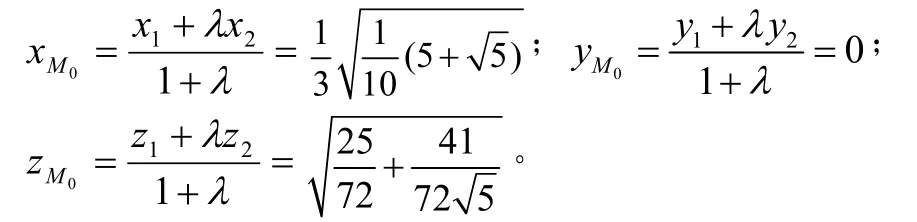
坐标M （0 1 1(5 5) 3 10 + ，0，25 41 72 72 5 + ）M （1 1 1(5 5) 6 10 − ，1 1(3 5) 6 2 + ，25 41 72 72 5 + ）M （−+，+ ），16 2 12 1 25 41 72 72 5 65 M （−+，+ ）12 1− ，25 41 72 72 5 65 3 16 M （+）1 1(5 5) 6 10 − ，− +，4 1 1(3 5) 62 25 41 72 72 5

对于足球体的其它顶点坐标都可以运用定比分点公式按同样的方法求得，这里不再机械性的重复。

3.足球体群

足球体可以由正二十面体对称切割而成，它传承了正二十面体的诸多性质。所以首先来了解一下正二十面体群，把正二十面体中心放在空间坐标原点，则正二十面体的位置可由一条棱的位置来确定，每个对称变换可由这条棱在变换后的新位置来描述，经过对称变换这条棱可置于 30条棱中的任何一条位置，再考虑棱的两种取向，因此正二十面体群包含2×30=60个元素，正二十面体群的阶数为60。

3.1 足球体群的元素。通过对正二十面体群的研究可得足球体群的阶数为60。由图2可得：由Bj指向Aj的六个轴都是足球体的五次转动轴，绕它们转动的变换分别记为Tj，其中两个相对侧面中心的连线都是三次转动轴，绕它们转动的变换分别记为Rj，其中1≤j≤10；两个相对棱的中点的连线都是两次转动轴，饶它们转动π的变换分别记为Sj，其中1≤j≤15。足球体具有很高的对称性。通过简单的空间变换很容易得到，五次转动使所有五次轴和所有三次轴分别互相等价且都为双向轴，所有二次轴也互相等价，因此足球体群包含五个类：恒元构成一类，15个二次轴转动元素Sj构成一类， 绕10个三次轴转动角的元素构成一类，绕6个五次轴转动角的元素构成一类，转动角的元素构成另一类。它们包含的元素数目分别是1，15，20，12和12，足球体群没有非平庸的不变子群， 但是足球体群有一个明显的子群D5它由z沿轴的五次转动和处于xy平面的五个二次轴转动元素组成。

3.2 分解为循环子群的乘积。在群论中，经常把点群表达成按一定次序排列的若干循环子群的乘积形式。这些循环子群元素的乘积不一定能交换，但它们的乘积没有重复。把它们的元素按给定次序乘起来，能唯一确定的表达群中每一个元素。

足球体群有相互垂直的二次轴，在三个互相垂直的二次轴的对称位置有三次轴，它们构成子群T。T群有12个元素，指数为5，陪集代表元素可以选T0的幂次。这样足球体群的每个元素都可以表达为的幂次和子群T元素的乘积，即其中都是循环群，足球体群元素表示为这四个循环子群的乘积形式结果见文[3]，又因为所以足球体群的生成元可以是和

4.小结

足球体不仅拥有美丽的几何外形与奇特的数学性质，而且具有丰富的应用价值。例如：把足球体的各个棱面进行适当的划分，就可以形成全部由三角形，并以不同方式组成的球形网架结构体系的几何形。这种空间结构不但可以用做大型公共建筑或某些大型工业建筑物的屋顶盖结构，也可以将每个面做成预置板块，经过拼装做成中小型旅游建筑、娱乐性建筑、临时性建筑的外围兼承重结构，乃至纪念性建筑或城市雕塑等的外观艺术造型。这样的结构既可以满足功能和造型要求，又便于预置安装、施工快、造价低，达到适用、经济、美观的效果，在2010年中国世博会的各国展馆中不乏其身影。

[1]薛党鹏.单位正多面体的体积探究[J].数学教学，2009.

[2]马中骐.物理学中的群论[M].科学出版社，2006.

[3]沈康身.历史数学名题赏析[M].上海教育出版社，2002.

Football’s structure and character

This article introduces the Football’s structure, then analyzes its geometry character, such as angle, volume, coordinates. Ultimately, Football group and its character are studied.

Football; structure; character; group;

徐兴国，男，扬州教育学院高邮校区数学系助教，华东师范大学在读硕士。

2010-07-23