支持向量机及其应用研究
林长方
(1.华侨大学计算机科学与技术学院 福建泉州 362021;2.漳州卫生职业学院信息技术部 福建漳州 363000)
支持向量机及其应用研究
林长方
(1.华侨大学计算机科学与技术学院 福建泉州 362021;2.漳州卫生职业学院信息技术部 福建漳州 363000)
文章在分析统计学习理论和支持向量机理论的基础上,分别从人脸检测和识别、说话人/语音识别、网络入侵检测、手写体数字识别及其他应用研究等方面对SVM的应用研究进行了综述,并讨论了SVM的优点和不足,展望了其应用研究的前景。
支持向量机;机器学习;统计学习理论
0.引言
支持向量机(Support Vector Machines或SVM)[1]是由贝尔实验室的Vladimir N.Vapnik博士等人在1995年基于统计学习理论基础上提出的一种专门研究小样本情况下的新型的机器学习方法。与传统统计学相比,SVM算法不是以经验风险最小化原则为基础的,而是建立在结构风险最小化原则基础之上的,是一种新型的结构化学习方法。SVM与神经网络、决策树不一样,它不是利用经验的启发式算法来修剪结构,而是通过改变一个控制参数来连续调节模型复杂度和结构,并且这种调节是自动的。可以说SVM是真正意义上的机构可以自动选择的学习机,它能很好地解决有限数量样本的高维模型的结构问题,具有良好的分类能力和预测性能。由于SVM在许多应用领域表现出较好的推广能力,自20世纪90年代提出以后,迅速引起各领域的注意和研究兴趣。目前对SVM的研究主要有以统计学习理论为基础的理论研究、各种改进的SVM方法、针对大型问题的有效算法以及各种应用领域的推广等。
1.结构风险最小化原则[2,3]
统计学习理论从理论上较系统地研究了经验风险最小化原则成立的条件、有限样本下经验风险与期望风险的关系(推广性的界)及如何利用这些理论找到新的学习原则和方法等问题。关于两类分类问题,它的结论是:对指示函数集中的所有函数(包括使经验风险最小的函数),经验风险 Remp(f)和实际风险R(f)之间至少 1-η的概率满足如下关系:

其中h是函数集的VC维,l是样本数。
结构风险最小化思想是把函数集S={f(x,w)}分解为一个函数子集序列(子集结构):S1⊂S2…⊂Sk⊂…⊂S,使各个子集按照 VC维的大小(Φ的大小)排列:h1≤h2≤…≤hk≤…,在每个子集中寻找最小经验风险,在子集间折中考虑经验风险和置信范围,以取得实际风险的最小,如图1所示。
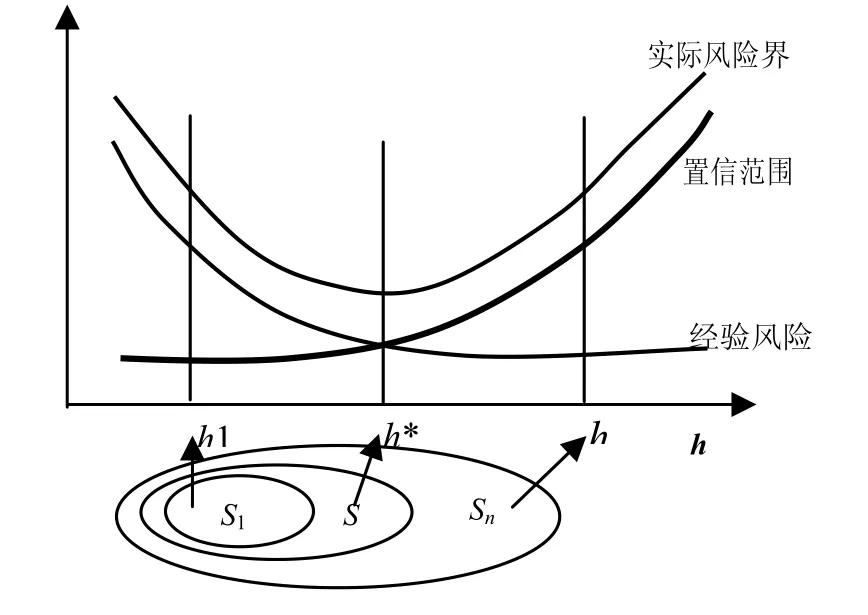
图1 结构风险最小化示意图
2.支持向量机
SVM最早应用于两类分类问题,其主要目标是寻找线性可分情况下的最优分类超平面,其基本思想可以用图2表示。图中实心、星号的两类点代表正、负两类样本。选定方向ω,取一个分类超平面H,平行移动H得到的两个极端位置H1和H2,都可以将正、负样本正确区分开,取H=(H1+H2)/2为最优分类超平面。H可以使正、负两类样本被正确分开,且分类间隔达到最大。

图2 线性可分情况
2.1 线性支持向量机。有两种情况:
2.2.1 线性可分情况。假设训练样本集:
T={(xiyi)|xi∈{-1,+1},i∈{1,…,l}}大小为l,由两个类别组成。若存在分类超平面H:(ω⋅x)+b=0,经适当变换得
根据点到直线的距离公式,超平面H1或H2上任意一点到H的距离为:|ω⋅x+b|/||ω||=1/||ω||。两超平面H1和H2之间的距离为2/||ω||,为使 H距离正负样本距离最大从而达到分类间隔最大就得使||ω||最小。那么,H可通过下面的正定二次规划来求解。

针对上面的二次规划问题有唯一的极小点,用Lagrange乘子法把(3)、(4)化成其对偶形式
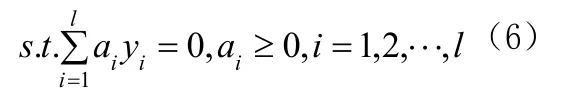
若ai>0,称相应的xi为支持向量。于是H为ai((yi(ω⋅xi)+b)−1)=0,而其采用分类决策函数为:
2.2.2 线性不可分情况。若训练集是线性不可分的,或事先不知道是否线性可分。于是在式(2)中加入非负变量ξi,使分类超平面H满足:
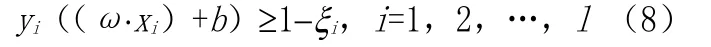
从而(3)、(4)函数变为:

这里ξi可看作训练样本关于(广义)分离超平面的偏差,ξi=0时问题变成线性可分情况,C>0是自定义的惩罚系数,用来控制样本偏差与机器泛化能力之间的平衡。
用Lagrange乘子法把(9)、(10)优化成其对偶形式

其中ai>0,i=0,1,…,l是每个样本对应的拉格朗日乘积因子。若ai>0,称相应的xi为支持向量,而其采用分类决策函数为:
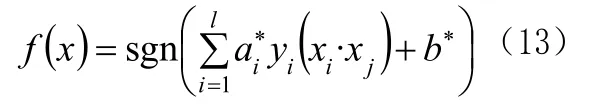
2.2 非线性支持向量机。对于非线性可分的分类问题,SVM的主要思想是将输入向量x映射到一个高维的特征向量空间H,并在H中构造最优分类面。即通过映射Φ使实心、星号代表的正负样本在高维特征空间中可以用线性判断函数分类。借助前面线性SVM超平面的求解,只需将公式中的x换成Φ(x),xi⋅xj变为非线性影射的内积Φ(xi)⋅Φ(xj)(可由满足Mercer定理的条件的核函数K(xi,xj)代替),就可以在特征空间上得到一个分类超平面。此时分类超平面改为(ω⋅Φ(x))+b=0,前面的(9)保持不变,(10)改为:s.t.yi((ω⋅Φ(xi))+b)≥1−ξi,从而构造非线性判别函数由(11)转化为:保持不变,决策函数(13)转化为:(即支持向量机)。
3.支持向量机的应用
SVM在理论上具有突出的优势,在实践应用方面最早由贝尔实验室针对美国邮政手写数字库的相关识别进行了研究,[1]取得了相对成功。在最近几年,有关SVM的应用研究得到了很多领域的学者的重视,在人脸检测和识别、说话人/语音识别、网络入侵检测、手写体数字识别及其他应用研究等方面取得了大量的研究成果,从最初的简单模式输入的直接SVM方法研究,进入到多种方法取长补短的联合应用研究,对SVM本身也进行了多方面的改进研究。
3.1 人脸检测和识别。即:任给一幅图像,判断其中是否存在人脸,如果存在,则返回人脸的位置、大小、位姿等。Osuna等[4]首先将SVM方法用于人脸检测与识别问题,取得了较好的实验结果。该方法使用了大量人脸样本和“自举”方法收集的“非人脸”样本来训练 SVM,并且使用逼近优化的方法减少支持向量的数量,在检测阶段对每个19×19像素的窗口使用SVM进行分类以确定是否为人脸。但直接使用SVM方法需要大量存储空间,且支持向量会较多(约占训练样本总数20%),速度较慢。为此,汪健等[5]提出一种递进式的人脸检测算法——背景消减、肤色分割与SVM方法相结合的人脸检测算法。尚凯等[6]提出了基于两级分类器和SVM的人脸检测研究,该方法中,第一级采用特征基方法,对待检测区域进行粗筛选,过滤掉大量非人脸背景信息,然后再用第二级SVM进行验证。实验结果表明这些算法都能提高检测速度,使系统更有效率。
人脸检测研究中更复杂的情况是姿态的变化。吴俊强等[7]提出基于LLE的彩色图象人脸检测,运用局部线形嵌入(LLE)的非线性降维方法,解决非线性结构的高维数据(图象)低维表示的问题,实现高维输入数据点映射到一个全局低维坐标系,同时保留了邻接点之间的空间关系。实验结果表明方法效率较高,而且不受姿态、表情和光照等影响。叶航军等[8]针对多姿态人脸检测的姿态判定提出了一种基于SVM的判定算法,将人脸姿态划成6个类别,从一个多姿态人脸库中手工标定训练样本集和测试样本集,训练基于 SVC和 SVR姿态分类器,分别取得 1.67%和 3.33%的分类错误率,其中SVC的分类效果明显优于传统方法中效果最好的ANN方法。
3.2 说话人/语音识别。说话人识别是根据语音波形中反映说话人生理和行为特征的语音参数,自动鉴别说话人身份的一项生物认证技术,贝尔实验室在20世纪50年代开发了第一个识别10个英文数字的语音识别系统——Audry系统。在过去的十几年里,SVM被证明是说话人识别的一种有效方法。[9]它可以达到,甚至超过动态时间规整(DTW)、语音信号线性预测编码(LPC)、隐马尔科夫模型(HMM)、人工神经元网络(ANN)等识别方法的效果。但是当训练样本集增大或噪音等因素影响,SVM的效率会明显下降。为此,赵振东等[10]提出基于VQ―SVM的说话人识别系统研究,将SVM在矢量量化(VQ)系统上进行二次识别来提高噪声环境下的说话人识别率,实验结果表明该方法可提高识别效率。丛菡菡[11]则针对训练样本增大效率降低的情况提出了基于双分界面的 SVM(TWSVMs)的说话人识别系统的研究,该识别系统在建立模型的过程中使用高斯混合模型进行特征提取,有效地减少了数据集的规模,取得更高的识别率,且对环境具有良好的鲁棒性,降低了算法的时间复杂度。
3.3 网络入侵检测。网络入侵检测系统主要处理多类攻击数据和正常数据,关键在于正常和异常行为模式库的建立。以往常用方法包括神经网络、数据挖掘等,然而这些方法需要大量的训练样本,实际操作不可能满足,容易导致误检率和漏检率偏高。现由于 SVM本身所具备的优势而被广泛用于入侵检测系统,取得良好的检测效果。[12]目前应用于入侵检测的SVM主要有二分类SVM、N分类SVM、针对无标记数据分类以及大量训练样本的 SVM。徐文龙等[13]提出的直推式支持向量机(TSVM)就是一种针对无标记样本的 SVM,它是一种不依赖于推广性思想的经验推理,基本思想是把未标记样本的特征加入到入侵检测算法的设计中去,弥补传统的归纳式支持向量机(ISVM)带来的缺陷。而针对了大量训练样本SVM导致的分类速度过慢,曾志强等[14]提出了基于约简SVM的网络入侵检测模型,方法是在特征空间中对支持向量进行聚类,寻找聚类质心在输入空间中的原像,将其作为约简向量,以实现支持向量削减。
3.4 手写体数字识别。手写体数字识别是光学字符识别技术(OCR)的一个分支,主要研究如何利用计算机自动辨认人手写在纸张等介质上的阿拉伯数字。现在的识别方法很多,如基于模板匹配或结构特征的方法、使用模糊推理的方法、基于矩和变换的方法、基于神经网络的方法等。贝尔实验室最先利用SVM对美国邮政手写体数字库进行实验,[1]人工识别平均错误率为 2.5%,基于神经网络(五层)识别错误率为5.1%,而利用三种SVM方法(分别采用3种核函数)针对直接采用16×16的字符点阵形式输入的数据识别错误率为4.0%、4.1%和4.2%,实验结果表明SVM的优越性能。如今在数字识别研究中越来越关注对特征的提取以提高识别效率。柳回春等[15]针对UK心理测试自动分析系统的手写体数字识别问题,利用结构特征和统计特征相结合,组合SVM与RBF神经网络等其它方法,实验表明该方法合理有效。夏国恩等[16]利用局部特征向量与全局特征向量提出了一种基于组合特征的手写体数字识别方法,采用USPS字库进行测试,结果表明识别效率明显优于其他方法。
3.5 其他应用。由于SVM的优越性,使其在其他很多方面也得到广泛应用。彭玉林[17]提出了SVM在遥感图象分析与处理中的应用。董本清[18]进行了SVM在工程领域的应用研究,主要针对SVM参数优化问题提出了一种基于混沌粒子群的核参数优化方法,通过收集寻找并生成数据集,利用SVM进行分类以及回归,实现SVM在工程领域的应用。李素梅等[19]针对VBR视频信号所具有的时变性、非线性和突发性等特点,提出了一种用于VBR视频通信量预测的差分输入SVM网络模型,实验结果表明:SVM网络模型的预测误差为0.0018,而梯度径向基函数神经网络模型的预测误差为0.0029,可见SVM网络模型的预测精度提高约40%。其他如应用SVM进行文本分类,[20]应用SVM进行气候预报[21]等。同时注意到近年来,SVM在基因工程,化学化工等方面也取得了很多有益的应用研究成果。
4.结论与讨论
SVM以统计学习理论为坚实基础,具有很多突出的优越性能:如基于结构风险最小化,克服了传统方法的过学习和陷入局部最小的问题;存在全局优化、泛化性能好;算法复杂度与特征空间维数无关等。但是作为一种新技术,SVM也存在着很多局限性,有很多问题还需要深入研究。
4.1 核函数及其参数对SVM的推广性能有很大影响,针对一个具体问题,使用哪种类型的核函数并找到一组最优(或次优)的核参数对应用成功与否至关重要。因此,如何快速、自动、准确地确定与数据匹配的核参数是一个值得深入研究的问题。
4.2 求解问题的速度和规模制约SVM的应用。线性SVM由于自身特点,能够设计出更好的训练算法,不仅速度快而且能处理规模达到百万的数据,而在设计非线性SVM训练算法,尤其是处理大规模数据的快速算法,是今后要重点关注的问题。虽然增量学习算法在处理大规模问题、实时问题方面有优势,如黄启春等[22]就为了扩展SVM在大规模数据集和成批出现数据领域的应用提出了基于支持向量机的增量式算法,取得一定的成果,但总体上研究进展还不大。
4.3 需加强对SVM规则抽取的研究。SVM与神经网络一样都属于暗箱模型,即缺乏输出结果的解释性,它不象决策树可以很容易地从决策树中抽取逻辑规则。
4.4 现有SVM理论仅讨论具有固定惩罚系数C的情况,而实际上正负样本的两种误判往往造成损失是不同的。
4.5 SVM在实际应用中的性能取决于特征提取的质量和SVM两方面,特征提取是获得好的分类的基础。为此,汪廷华等[23]就针对现有的加权支持向量机(WSVM)和模糊支持向量机(FSVM)只考虑样本重要性而没有考虑特征重要性对分类结果的影响的缺陷,提出了基于特征加权的支持向量机方法。但对特征提取的研究还没有引起足够的重视。
可见SVM在目前仍然存在很多问题需要进一步的研究,但由于其本身所具有的独特优越性,我们有理由相信SVM的理论和应用研究都有着广泛的前景。
[1]边肇祺,张学工.模式识别[M].清华大学出版社,2000.
[2]Vladinir N. Vapnik. The Nature of Statistical Learning Theory-Second Edition. Springer-Verlag,New York,2000.
[3]Vapnik V.统计学习理论[M].许建华,张学工,译.电子工业出版社,2004.
[4]Osuna E,Freund R,Girosi F. Training support vector machines:an application to face detection[C].Proceedings of the Computer Vision and Pattern Recognition.Puerto Rico,1997,P130-136.
[5]汪健,张虹.MSSFD——种递进式人脸检测算法[J].微电子学与计算机,2007(12).
[6]尚凯,徐东平,于红芸.基于两级分类器和SVM的人脸检测研究[J].计算机与数字工程,2008(11).
[7]吴俊强,周激流,何坤.基于LLE的彩色图象人脸检测[J].四川大学学报(自然科学版),2006(4).
[8]叶航军,白雪生,徐光.基于支持向量机的人脸姿态判定[J].清华大学学报(自然科学版),2003(1).
[9]Collobert R,Bengio S. SVMTorch:Support vector machines for large-scale regression problems[J].Journal of Machine Learning Research,2001(1),P143-160.
[10]赵振东,胡喜梅,田景峰.基于 VQ—SVM的说话人识别系统[J].华北电力大学学报,2009(5).
[11]丛菡菡.基于TWSVMs的改进说话人识别系统[J].实验科学与技术,2008(2).
[12]Batur C,Zhou L,Chan C C. Support vector machines for fault detection[C].//CDC2002.Proceedings of the 41st IEEE Conference on Detection and Control. Las Vegas:IEEE computer society press,2002,P1355-1356.
[13]徐文龙,姚立红,潘理,等.基于TSVM的网络入侵检测研究[J].计算机工程,2006(18).
[14]曾志强,高济,朱顺痣.基于约简 SVM的网络入侵检测模型[J].计算机工程,2009(17).
[15]柳回春,马树元,吴平东,等.UK心理测试自动分析系统的手写体数字识别[J].北京理工大学学报,2002(5).
[16]夏国恩,金炜东,张葛祥.基于组合特征的手写体数字识别方法[J].计算机应用研究,2006(6).
[17]彭玉林.支持向量机在遥感图像分析与处理中的应用[J].通信技术,2008(9).
[18]董本清.支持向量机在工程领域的应用研究[D].湖南大学,2007.
[19]李素梅,张延,常胜江.用支持向量机网络实现 VBR视频通信量的预测[J].电子学报,2006(2).
[20]杨霞,宋顺林.基于加权近似支持向量机的文本分类研究[J].计算机工程与设计,2009(15).
[21]韦惠红,李才媛,邓红,等.SVM方法在武汉区域夏季暴雨预报业务中的应用[J].气象科技,2009(2).
[22]黄启春,刘仰光,何钦铭.基于支持向量机的增量式算法[J].浙江大学学报(工学版),2008(12).
[23]汪廷华,田盛丰,黄厚宽.特征加权支持向量机[J].电子与信息学报,2009(3).
Support Vector Machines and Application Research
Based on the analysis of Statistical Learning Theory(SLT)and Support Vector Machine (SVM), the article makes a review of the application research of SVM from the perspectives of face detection and recognition, speaker or speech recognition, network intrusion detection, handwritten digit recognition, etc. With the discussion of advantages and disadvantages of SVM, the prospect of its application research is also expected.
Support vector machine; Machine learning; Statistiacl learning theory
林长方(1978-),男,福建漳州人,在读硕士,漳州卫生职业学院信息技术部讲师,主要从事数据库技术、机器学习研究。
2010-06-23

