基于直觉模糊集算子的多属性群决策方法

吴怀岗，张 晴

（1.南京大学 工程管理学院，南京 210008；2.南京师范大学 计算机科学与技术学院，南京 210046）

0 引言

随着社会问题的日益复杂化以及科学研究的不断深入，传统的模糊集理论因其不能完整地表达所研究问题的全部信息而在实际应用中受到越来越多的制约和挑战[1]。Atanassov[2]对传统的模糊集进行了拓展，提出了直觉模糊集的概念。由于直觉模糊集同时考虑了隶属度、非隶属度和犹豫度这三方面的信息，使得它在对事物属性的描述上提供了更多的选择方式，在处理不确定信息时具有更强的表现能力，因此直觉模糊集理论在学术界及工程技术界引起了广泛的关注。文献[3]对直觉模糊集环境下的几何集结算子进行了研究，提出了直觉模糊加权几何(IFWGA)算子，直觉模糊有序加权几何(IFOWGA)算子和直觉模糊混合几何(IFHG)算子，并且基于IFHG算子，给出了相应的决策方法。文献[4]对直觉模糊集环境下的算术集结算子进行了研究，提出了直觉模糊算术平均(IFAA)算子和直觉模糊加权算术平均(IFWAA)算子，并且基于IFAA算子和IFWAA算子，给出了相应的群决策方法。文献[5]给出模糊数直觉模糊集两个改进算子,在此基础上,提出用精确函数解决记分函数无法决策的问题,以保证记分函数的严密性与合理性。文献[6]针对模糊数直觉模糊信息的集成问题，提出一种属性权重确知且属性值以模糊数直觉模糊数形式给出的多属性群决策方法。本文拟将传统的topsis方法与灰关联分析方法相结合，并且引入直觉模糊集理论，以期为解决多属性群决策问题提供一个新的方法和思路。

1 直觉模糊集理论

直觉模糊集由Atanassov提出[2]，是传统模糊集的一种扩充和发展。直觉模糊集增加了一个新的属性参数：非隶属度函数，它能够更加细腻地描述和刻画客观世界的模糊性本质。

定义1[2]设X是一个非空经典集合，X={x1,x2,…，xn}，X上形如A={＜x,uA(x),vA(x)＞|x∈X}的三重组称为X上一个直觉模糊集。其中uA(x),vA(x):X→[0,1]，均为X的隶属函数，且0≤uA(x)+vA(x)≤1，这里uA(x),vA(x)分别是X上元素x属于A的隶属度和非隶属度，表示为支持元素x属于集合A的证据所导出的肯定隶属度的下界和反对元素x属于集合A的证据所导出的否定隶属度的下界。

对于X上的每一个直觉模糊集，称πA(x)=1-uA(x)-vA(x)为直觉模糊集A中元素x的直觉指数，表示元素x属于A的犹豫度。 显然，0≤πA(x)≤1，x∈X。

定义 2 A={＜x,uA(x),vA(x)＞|x∈X},B={＜x,uB(x),vB(x)＞|x∈X}为任意两个直觉模糊数，则

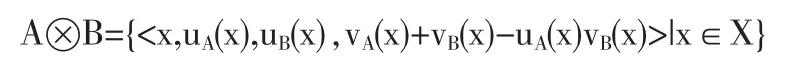
定义3 设Q为直觉模糊集，Aj=(uj,vj,πj)为一组直觉模糊数，wj为其权重，满足 wj∈[0,1]和

令 IFWA：Qn→Q，若

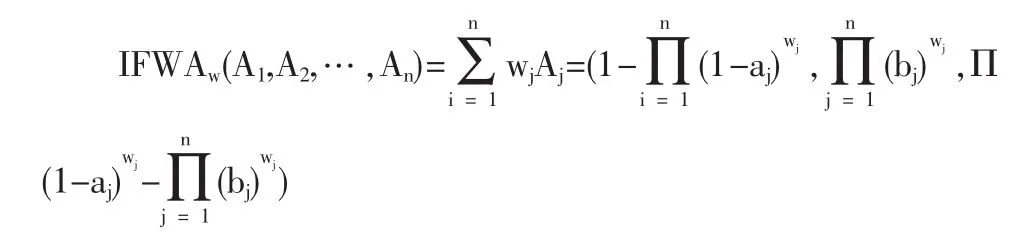
则称函数IFWA为n维直觉模糊加权平均算子。

2 基于直觉模糊集算子的多属性群决策方法

设 A={A1,A2,…，Am}为方案集，X=(X1,X2,…，Xn)为属性集，下面结合传统topsis法和灰关联分析法，给出一种解决多属性群决策问题的方法。

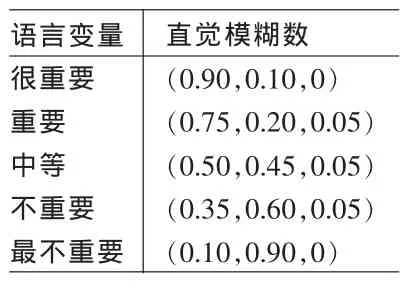
表1 语言变量表示重要性

表2 语言变量表示属性值

表3 决策者重要性

步骤1：确定每个决策者的权重

假定组成决策小组的决策者有l个，决策者的重要性用语言变量表示，见表1。

设Dk=(uk,vk,πk)为第k个决策者的权重，用下面的公式将直觉模糊数转化为实数：

步骤2：构造决策矩阵

在群决策中，所有的个体决策得出的决策矩阵必须进行集结，得到最终的综合所有决策者意见的决策矩阵。设R(k)=为每个决策者的决策矩阵，本文利用直觉模糊加权平均算子进行集结，得到矩阵R=(rij)m×n，其中

这里：

本文用语言变量表示属性值，见表2。

步骤3：决定属性权重

每个决策者心中属性的权重也不一定相同，所以我们也需要利用直觉模糊加权平均算子对权重进行集结。设为第k个决策者赋予属性的权重值，则集结所有决策者的权重值，得出最终属性权重

所有属性权重 W=[w1,w2,…，wn]。

步骤4：加权决策矩阵

将权重与决策矩阵相乘，得出加权矩阵R'：

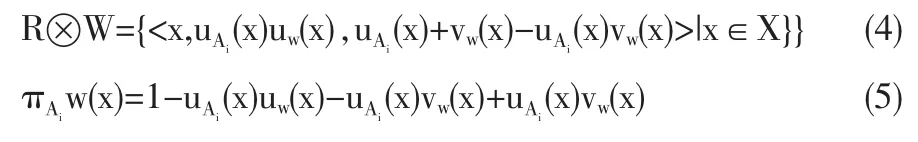
步骤5：确定正理想解

设J1和J2分别表示效益型、成本型的下标集，可用下列公式确定正理想解A*=(uA*W(xj)，uA*W(xj))，其中

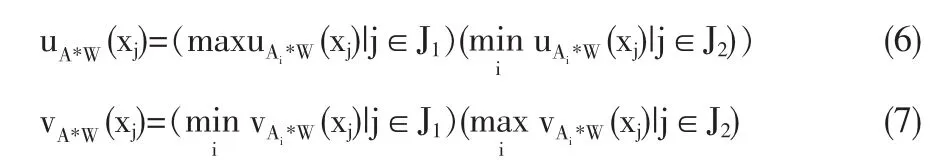
步骤6：计算各方案与理想解的关联度

根据灰色关联分析方法可知[7～9]，方案和理想最优方案A*关于指标Xj的关联系数为

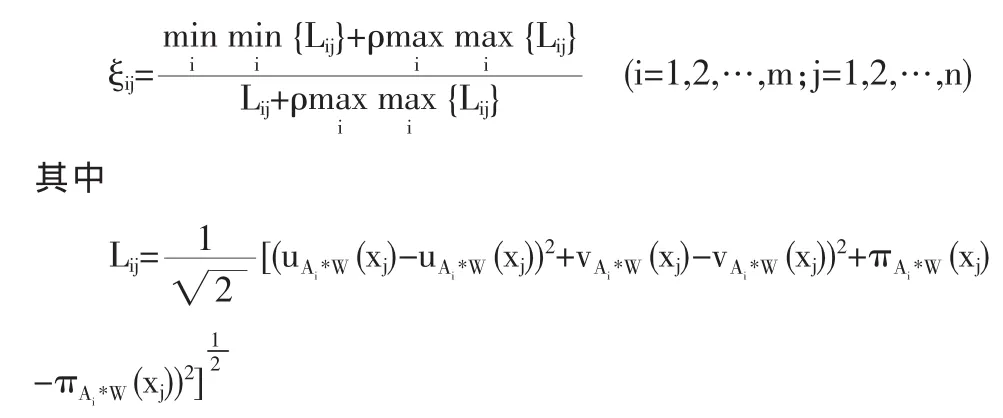
为(uAi*W(xj),vAi*W(xj),πAi*W(xj))到理想解(uAi*W(xj),vAi*W(xj),πAi*W(xj))的距离；ρ 为分辨系数，ρ∈[0,1]，一般取值 0.5。

则各方案与理想最优方案的关联系数矩阵为

方案Ai与A*的综合关联度为

显然，ξi越大，表示被评价方案Ai与理想最优方案A*越接近，即决策方案Ai越佳。因此，各方案按综合关联度ξi大小对方案进行排序，即可得到决策方案集中的最优方案。

3 应用实例

某汽车生产商欲选择一家最合适的重要零部件供应商，经初步筛选，现有5个供应商可供选择,包括A1、A2、A3，A4,A5。为进行科学有效地评估，公司成立了一个3人评选委员会，包括 DM1、DM2、DM3，考虑如下 4 项指标：产品质量 X1，合作程度X2，运输能力X3，价格X4。经调查、评估，最后得出决策者权重（见表3），每个决策者对各属性的打分（见表4），以及决策者认为属性的重要性（见表5）。

步骤1：确定决策者属性权重

利用公式(1)，计算得出每个决策者权重，见表6。

步骤2：利用公式（2），得到集结后的决策矩阵，见表7。

步骤3：根据表5，利用公式（3），得出属性权重如下：

步骤 4：利用公式（4）、（5），得出加权矩阵，见表 8。

表4 决策者对各属性的打分

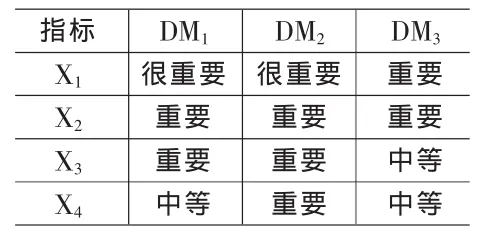
表5 属性的重要性

表6 决策者权重

步骤5：X1,X2,X3为效益型指标，X4为成本型指标，根据公式（6）、（7）得出正理想解为：

A*={(0.731,0.215,0.054),(0.575,0.294,0.121)(0.530,0.353,0.117),(0.303,0.606,0.091)}

步骤6：计算各方案与理想解的关联度

各方案与理想最优方案的关联系数矩阵为

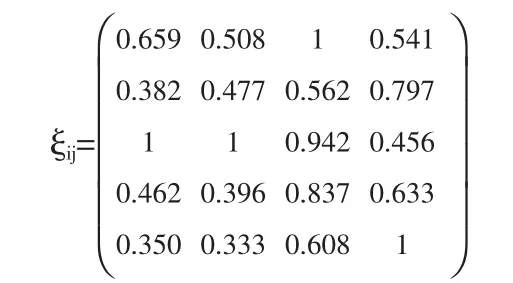
方案Ai与A*的综合关联度为

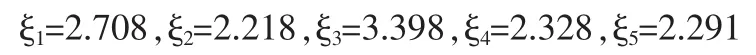
根据 ξi大小对 5 个供应商进行排序：A3＞A1＞A4＞A5＞A2，即供应商A3是汽车生产商的最佳选择。

4 结语

在群决策情形下，本文将直觉模糊加权平均算子应用于属性值和属性权重的集结；同时，本文将传统的topsis法与灰关联分析方法相结合，不直接计算各方案与理想解的距离，而用灰关联度的大小确定方案的优劣，为解决不确定多属性群决策问题提供了一种新的方法和思路。实例应用研究表明该方法客观科学，在解决项目选择、制造业等存在不确定因素的管理决策问题中简单实用。

表7 决策矩阵

表8 加权矩阵

[1]胡辉,徐泽水.基于Topsis的区间直觉模糊多属性决策法[J].模糊系统与数学,2007,21(5).

[2]Atanassov K.Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,1986,20(1).

[3]Xu Z S,Yager R R.Some Geometric Aggregation Operators Based on Intuitionistic Fuzzy Sets[J].International Journal of General System,2006,35（4）.

[4]Xu Z S.Intuitionistic Preference Relations and Their Application in Group Decision Making[J].Information Science，2007,177(11).

[5]刘於勋.基于模糊数直觉模糊集算子的多准则决策方法[J].现代电子技术，2009，（6）.

[6]汪新凡.模糊数直觉模糊几何集成算子及其在决策中的应用[J].控制与决策，2008,23(6).

[7]刘思峰,郭天榜,党耀国.灰色系统理论及其应用[M].北京:科学出版社,1999.

[8]邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社,1987.

[9]Zhang J J,Wu D S,Olson D L.The Method of Grey Related Analysis to Mu1tiple Attribute Decision Making Problems with Interval Numbers[J].Mathematical and Computer Modeling，2005,42(9).