基于CRITIC权重与TOPSIS模型的节水灌溉方案优选

邓丽娟，马爱玲

（1.新疆水利水电科学研究院，乌鲁木齐830049；2.新疆天山源水管理经营有限公司，乌鲁木齐 830049）

当前，我国各地正在大规模发展节水灌溉技术和建设节水灌溉工程。为了避免在发展过程中产生盲目性，造成人力、物力的浪费，做好节水灌溉工程方案的优选，对节水灌溉技术的选择及进行科学决策具有重要意义。

节水灌溉工程方案优选就是从若干个建设方案中，经过系统分析、评价，从中选择出最佳方案即最优方案。节水灌溉方案的优选可以从技术、经济和社会等几个方面考虑，例如按投资、经济效益、投资偿还年限、工程寿命等指标，而这些指标又具有不相容性和模糊性［1～2］，这给优选带来一定的困难。为此，本文利用CRITIC权重 （Criteria Importance Through Intercriteria Correlation，简称CRITIC）与TOPSIS（Technique for order preference by similarity to ideal solution）法将这些指标综合成单一指标，并用实例加以说明。

1 TOPSIS模型简介［3～8］

1.1 模型原理

TOPSIS法的基本思路是定义决策问题的理想解和负理想解，然后在可行方案中找到一个方案，使其距理想解的距离最近，而距负理想解的距离最远。理想解一般是设想最好的方案，其所对应的各个属性至少达到各个方案中的最好值；负理想解是假定最坏的方案，其对应的各个属性至少不优于各个方案中的最劣值。方案排队的决策规则，是把实际可行解和正理想解与负理想解作比较，通过计算某一方案与最好方案和最劣方案间的加权欧氏距离，得出该方案与最好方案的接近程度，以此作为评价各方案优劣的依据。若某个可行解最靠近理想解，同时又最远离负理想解，则此解是方案集的满意解。

1.2 模型计算步骤

1.2.1 形成决策矩阵

设多指标决策问题的方案集为M=（M1，M2，…，Mm），指标集为C=（C1，C2，…，Cn），方案Mj对指标Ci的值记为xij（i=1，2，…，m；j=1，2，…，n），则可形成多目标决策矩阵X：

1.2.2 无量纲化决策矩阵

为了消除各指标量纲不同对方案决策带来的影响，需要对形成的决策矩阵进行无量纲化处理，构建标准化决策矩阵V=（υij）m×n，无量纲化处理可以采用以下形式：

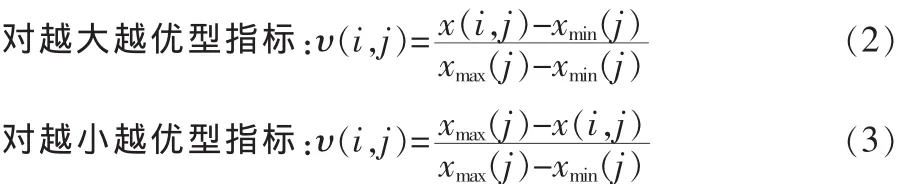
式中 υ（i，j）为指标特征值归一化值，xmin（j）、xmax（j）分别为方案集中第j个评价指标的最小值和最大值。

通过式（2）和式（3）得到的x（i，j）统一为［0，1］区间上的评价指标。

1.2.3 构建加权决策矩阵

将形成的无量纲化矩阵与各指标的权重相乘，可得到加权决策矩阵：R=（rij）m×n

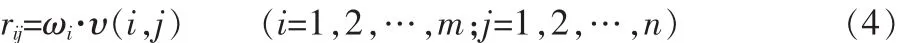
1.2.4 计算理想解和负理想解

根据已构建的加权决策矩阵，可以确定各方案的理想解S+与负理想解S-：

1.2.5 距离的计算

在计算与理想解和负理想解的距离时，一般采用欧氏距离，其计算公式：

1.2.6 贴近度的计算及方案决策

根据数学模型计算相对接近程度值ξi，其值在0与1之间，该值越接近于1，表示评价对象越接近最优水平。根据相对接近程度值ξi对多个评价对象进行评价排序。

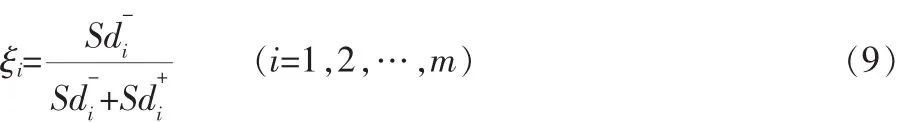
根据ξi值的大小排序，ξi越大则方案Mi越接近理想解，方案越优。

2 CRITIC法求解指标权重

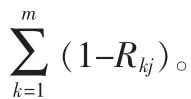
式中 Rkj表示第k个特征和第j个特征之间的相关系数。

3 应用实例

某节水灌溉工程有管道灌溉、喷灌、滴灌、小管出流灌溉4个建设方案（分别为方案A、B、C、D）供选择，各方案评价指标见表 1［10］。

表1 各方案评价指标值

计算步骤如下：

（1）利用（2）、（3）式计算规范化矩阵。

（2）利用CRITIC法确定评价指标权重，见表2。

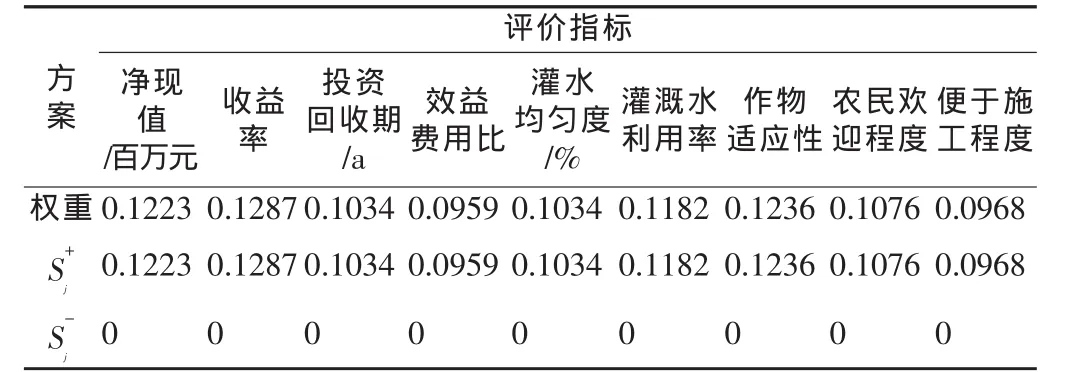
表2 各评价指标权重

表3 评价结果

由表3可知，max（ξi）=0.5378，即方案A为最优方案，这与文献［10］研究结果完全相同。

4 结语

（1）方案优选是一个复杂的决策问题，涉及的评价因素众多。本文构建的TOPSIS评价模型采用CRITIC法，综合考虑各评价指标特征值之间的差异，在减小人为赋权的主观性影响的同时，避免指标权重分配的均衡化。

（2）计算结果表明，该模型计算简单，便于操作，决策结果较为客观可靠，为节水灌溉工程方案优选提供了科学依据。

［1］严乐军.模糊综合评判法在节水灌溉项目投资决策中的应用［J］.节水灌溉，2000，（4）：11-13.

［2］肖芳淳.优选油气田开发方案的模糊物元分析［J］.石油勘探与开发，1997，24（2）：84-87.

［3］汤光华.对TOPSIS法的评价与扩展［J］.浙江统计，1998，（2）：12-14.

［4］华小义，谭景信.基于“垂直”距离的TOPSIS法——正交投影法［J］.系统工程理论与实践，2004，（1）：114-119.

［5］王新玲.建筑工程方案模糊层次综合优选模型和方法［J］.建筑结构，2000，30（8）：60-63.

［6］谢季坚，刘承平.模糊数学方法及其应用［M］.武汉：华中科技大学出版社，2000.

［7］邱菀华.管理决策与应用熵学［M］.北京：机械工业出版社，2001.

［8］闫文周，顾连胜.熵权决策法在工程评价中的应用［J］.西安建筑科学大学学报，2004，36（1）：98-100.

［9］Diakoulaki D， Mavrotas G， Papayannakis L.Determining objective weights in multiple criteria problems：The critic method［J］.Computers&Operations Research，1995，22（7）：763-770.

［10］门宝辉.选择节水灌溉方式的灰色关联投影法［J］.沈阳农业大学学报，2004，35（5）：476-479.