基于熵权的灰色关联模型在水电工程评价中的应用

邱红霞

（新疆兵团农一师勘测设计院，新疆 阿克苏 843000）

伴随着灰色系统理论的出现和发展，灰色关联分析逐渐成为一种应用广泛的评价方法，影响评价结果的重要因素是在评价中如何合理确定指标的权重。本文通过将信息熵引入到灰色关联分析模型的权重计算中，尽量消除权重计算中的人为干扰，以提高该评价方法的评价精度，使评价结果更客观，更符合实际，为多指标水电工程综合评价提供新的方法。

1 基于熵权的灰色关联模型

1.1 灰色关联分析［1～7］

1.1.1 确定分析序列

考虑多指标决策域的集合为A，A={方案1，方案2，…，方案m}={A1，A2，…，Am}，各方案评价指标集合为V，V={V1，V2，…，Vn}。记方案Ai对评价指标Vj的属性值为Xij（i=1，2，…，m；j=1，2，…，n）。

1.1.2 决策矩阵的构建

在评价前，为了消除指标量纲的不同所带来的不可公度性，需要进行无量纲化处理。指标可分为效益型和成本型：效益型指标是指属性值愈大愈好的指标，一般情况下，指发电量、投资净现值等；成本型指标是指属性值愈小愈好的指标，如投资回收期、投资等。设相对最佳方案的指标为A0j，且满足以下条件，当因素指标Vj为效益型指标时，X0j=max（X1j，X2j，…，Xmj）；当因素指标Vj为成本型指标时，X0j=min（X1j，X2j，…，Xmj）。 令：

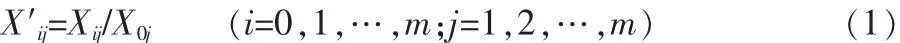
通过无量纲化处理可得到相应的无量纲矩阵：

此时，称含有相对最佳决策方案的增广型矩阵X=（Xij）（m+1）×n，（i=0，1，…，m；j=1，2，…，n）为方案集合A对指标V的决策矩阵。

1.1.3 求绝对差序列及两极最小差、最大差

绝对差序列：

两极最小差值：

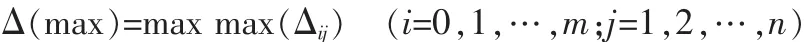
两极最大差值：

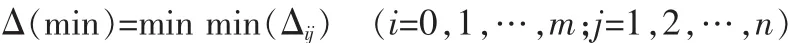
1.1.4 计算关联系数

第i方案第j项指标值的关联系数（表征比较数列与标准数列的某一点上的关联性）ξij可以定义为：

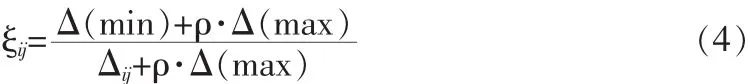
式中 ρ为分辨系数，其值在［0，1］之间，一般取0.5。

1.2 用熵值法求解指标权重［8～10］

对项目指标权重的确定一般多采用AHP方法，这是一种基于专家打分的主观确定权重的方法，这样就容易造成评价结果可能由于人的主观因素而形成偏差，甚至结论错误。熵值法能较客观地反映数据本身的信息有序性，通过评价指标值构成的判断矩阵来确定指标的权重，这样能尽量消除各因素权重的主观性，使评价结果更符合实际。其计算步骤：

（1）构建m个方案n个评价指标的判断矩阵:

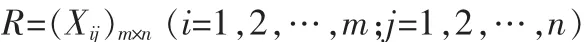
（2）将判断矩阵归一化处理，得到归一化判断矩阵B：

式中 Xmax、Xmin分别为同指标下不同方案中最满意者和最不满意者（越小越满意或越大越满意）。

（3）根据熵的定义，m个方案n个评价指标，可以确定评价指标的熵为：

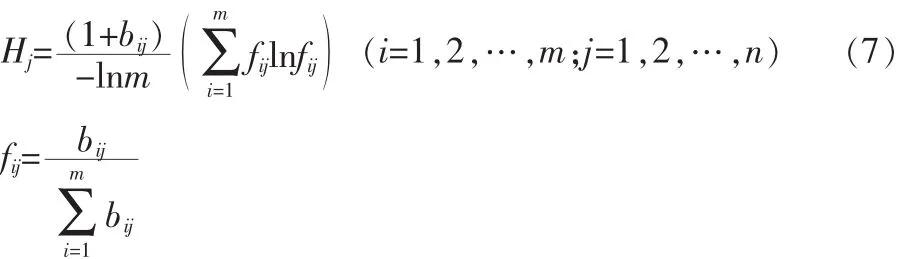
为使lnfij有意义，一般需要假定当fij=0时，fijlnfij=0。但当fij=1，lnfij=0，这显然不切合实际，与熵所表述的含义相悖，故需对fij加以修正，将其定义为：

计算评价指标的熵权W：

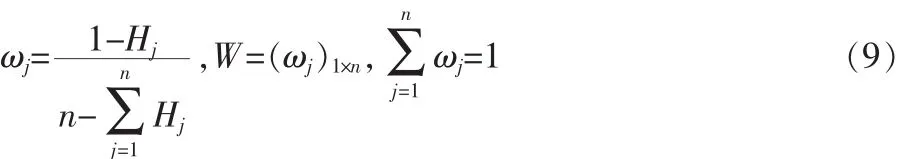
1.3 计算关联度

关联度Ei是指被评价方案与标准方案两者互相接近的程度，其值越大表示两者越接近，反之则相离较远。从而，可以根据关联度的大小对各方案进行优劣排序，也可以根据标准值的关联度进行分类。Ei可以表示为：

2 实例分析

某水电工程建设项目有4个待选投资方案，利用9个指标对各方案进行评价，得到的相关数据见表1［11］。

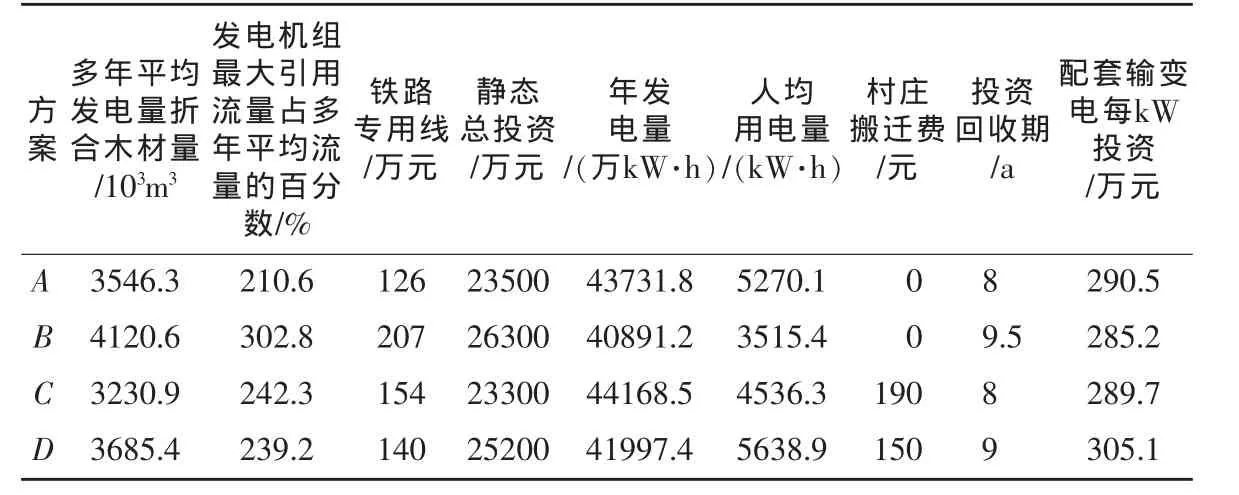
表1 各方案的主要技术经济指标

2.1 构建决策矩阵

将表1中数据进行无量纲化处理，构成判断矩阵X（由于该矩阵第一行元素均为1，故未列出）：

2.2 构建关联系数矩阵

根据式（3）和式（4）计算关联系数，构建关联系数判断矩阵ξ：

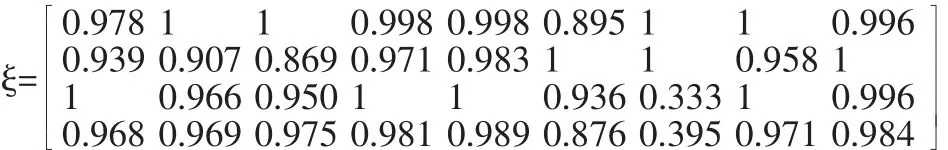
2.3 用熵值法计算权重系数

根据式（5）和式（6）构造归一化判断矩阵B：

由式（7）、（8）、（9）计算可得熵Hj=（0.9794，0.9796，0.9786，0.9741，0.9748，0.9746，0.9693，0.9720，0.9789） 和 ωj=（0.1115，0.1116，0.1114，0.1109，0.1110，0.1110，0.1104，0.1107，0.1115）。

2.4 方案关联度计算

由式（10）可以得到各方案的关联度Ei：

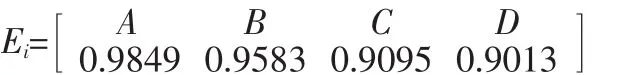
可知投资方案A为最优投资方案，这与文献［11］的研究结果完全一致。

3 结语

水电工程方案评价需要统筹考虑多目标的属性，其评价方法和准则至今尚未成熟。将基于熵权的关联度评价模型应用于对水电工程方案的综合评价中，引入熵权计算权重系数，可以有效地区分方案的优劣次序，且能够更科学全面地考虑各种主观信息。另外，该模型还可用于招投标和水资源利用程度综合评价等，具有较好的推广应用前景。

［1］党耀国，刘世峰，刘斌，等.基于动态多指标灰色关联决策模型研究［J］.中国工程科学，2005，7（2）：69-72.

［2］邓聚龙.灰色理论基础［M］.武汉：华中理工大学出版社，2002.

［3］罗党，刘思峰.灰色关联决策方法研究［J］.中国管理科学，2005，13（1）：101-106.

［4］门宝辉，赵燮京，梁川.多目标决策灰色关联投影法在水利工程开发中的应用［J］.武汉大学学报（工学版），2003，（4）：36-39.

［5］邱菀华.管理决策与应用熵学［M］.北京：机械工业出版社，2001.

［6］张庆华，白玉慧，倪红珍.节水灌溉方式的优化选择［J］.水利学报，2002，20（1）：47-51.

［7］吕锋，崔晓辉.多目标决策灰色关联投影法及其应用［J］.系统工程理论与实践，2002，（1）：103-107.

［8］周前祥，张达贤.工程系统设计方案多目标灰色关联度决策模型及其应用的研究［J］.系统工程与电子技术，1999，21（1）：1-31.

［9］李春晖，李爱贞.TOPSIS法在环境质量综合评价中的应用［J］.地质灾害与环境保护，1999，10（2）：9-13.

［10］闫文周，顾连胜.熵权决策法在工程评标中的应用［J］.西安建筑科技大学学报，2004，36（1）：98-100.

［11］杨开云，朱峰，王亮，等.灰色关联度模型在水利工程投资决策中的应用［J］.人民长江，2008，39（15）：90-91.