基于N次谐波法的供油凸轮型线的拟合

柴保明,张 浩,高维金,高学攀,谷兴海

(河北工程大学机电学院,河北邯郸056038)

柴油机供油泵主要依靠凸轮轴将高压燃油输送到各缸燃烧室,因此作为喷油系统中的重要零件之一,供油凸轮的轮廓形状直接决定着喷油规律的变化。针对凸轮型线的优化设计,通常采用多项式法、样条函数法等拟合的方法构造升程函数,来代替供油凸轮升程曲线进行理论分析[1]。

1 谐波法拟合凸轮型线的原理

凸轮升程函数s(φ)只要有适当的光滑性,就能得到对应凸轮转角 φ的一系列节点(φ0,φ1,…)的凸轮升程数据。根据傅里叶级数展开和收敛定理,s(φ)可在[-π,π] 区间上展开为傅里叶级数[6]

当j∈[1,n] 时,由式(1)得

若满足|Sn(φ)-s(φ)|＜ε,则可以近似认为Sn(φ)即为所求的升程函数s(φ)。当n增大时,拟合精度提高,当n→ ∞时,Sn(φ)=S(φ)。

2 凸轮型线拟合

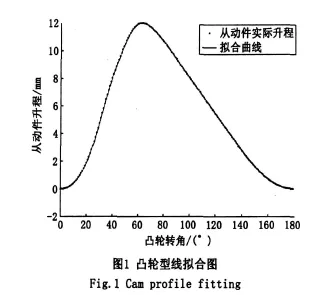
采用N次谐波函数对电控单体集成泵的凸轮型线进行了曲线拟合,凸轮升程按凸轮升程表[7]中所列的间隔提供,控制范围0°～ 180°,凸轮型线的基本参数如下:凸轮基圆直径为Dt=34mm,凸轮宽度=18mm,滚轮直径=22mm,滚轮宽度=17.5mm,最大升程h=12mm,对应的凸轮转角为63°,并通过MATLAB软件编程实现拟合如图1所示。

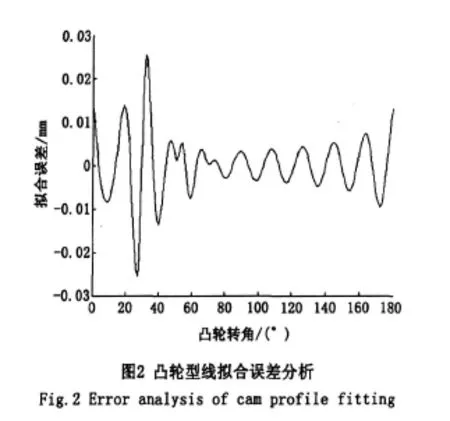
图2为拟合误差结果,除少数几个点之外,其他点都在误差允许范围内。原因可能是N的取值有限,出现了截断误差。虽然理论上项数N越大,精度越高,但由于在求解的过程中,需要采用数值积分方法近似求解,因此随着N的增大,积分的误差会增大,导致拟合结果与实际曲线的误差增大;另外升程表的取值也是误差出现的一个重要原因。

3 供油凸轮性能分析

为了便于研究该类凸轮机构运动规律的共同特性,我们把输入量角度 φ,位移 h、速度 v、加速度a等运动参量进行无因次处理,同时用大写字母表示这些无因次量[7]。

从数学理论的角度出发,只要满足狄氏条件,任何曲线均能展开成傅里叶级数的形式,故供油凸轮的滚轮体的速度、加速度、跃度分别可表示为

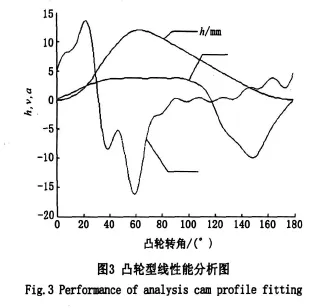
利用MATLAB软件对位移h、速度v、加速度a的变化规律进行拟合,由图3可以看出,当凸轮参照转速为1 500rpm、凸轮转角为33°时,速度达到最大值;在上升期,等速度区段较大,即凸轮工作段比较大,此时,速度上升比较平稳,循环喷油量比较稳定,同时加速度最大值也在一定的范围之内;在下降期加速度变化较小,从动件运行平稳、冲击小。

4 结论

1)N次谐波法对凸轮型线所规定的速度和加速度实现了定量控制,可以计算出准确的谐波函数供油凸轮型线。

2)凸轮升程表的间隔角度影响着N的取值,拟合过程中N的取值受限是造成截断误差的主要原因,因此可以适当地增大N值来获得较高的拟合精度。

3)MATLAB软件编程实现了凸轮型线拟合,可以直观的看出凸轮机构运动规律和特性,从而为凸轮优化提供了理论依据。

[1] 李友锋.N次谐波法拟合供油凸轮型线的讨论[J] .内燃机车,2006(4):15-17.

[2] 缪雪龙,张毅华.数值计算在凸轮型线分析中的应用[J] .内燃机燃油喷射和控制,2000(1):17-18.

[3] 吴勤.喷油泵凸轮型线的拟合[J] .拖拉机与农用运输车,2001(3):26-27.

[4] 严国建,刘永长,胡继泽.谐波函数供油凸轮速度特性的研究[J] .内燃机学报,1992(1):36-40.

[5] 石永刚,吴洋芳.凸轮机构设计与应用创新[M] .北京:机械工业出版社,2007.

[6] 杨东明.凸轮机构反求设计、误差分析与检测方法的研究[D] .昆明:昆明理工大学,2002.

[7] 葛正浩,丁英杰,徐峰.平面凸轮精密测量及运动规律反求设计新方法[J] .机械设计与研究,2008(1):32-35.