基于自记忆原理的深基坑位移预测方法
王 伟,谢学斌,黄 东
(中南大学 资源与安全工程学院,湖南 长沙410083)
对基坑变形进行准确的监测和有效的预测是基坑工程成败的关键因素之一[1]。目前采用较多的预测方法是利用深基坑位移监测时间序列,建立各类时序分析模型的方法。深基坑位移预测的时间序列方法主要有:灰色理论预测方法[2-3];时间序列分析方法[4],如AR模型,ARMA模型;智能算法[5-8],如BP神经网络算法,RBF神经网络算法,遗传算法;组合预测方法[9]。以上每种方法各有其适应条件及优缺点,如灰色理论模型适用于累加生成数列具有灰指数规律,但有一些时间序列的累加生成数列常常不具有灰指数规律,因此预测出的数据就会存在较大误差。
自忆性原理强调系统的前后承续性,强调系统自身演变对过去历史的依赖。也就是要预测未来,就得立足现在,回溯过去。对于只有一组时间序列值的系统,如深基坑支护系统一般只有一系列动态观测值,此时,可把现有观测资料看作描述实际非线性系统动力模式的一系列特解,通过反演计算得到描写系统的非线性动力模式。求得系统的动力模式后,建立自记忆模型进行系统模拟或预报[10]。这种方法不需要分析确定影响深基坑支护系统位移变化的主要因素,也不需要收集整理与深基坑支护系统位移动态观测序列相应的多种影响因素数据,避免了大量数据的收集整理,只涉及深基坑支护系统位移观测序列本身,方便实用且具有较好的预测精度。
1 系统自记忆原理与建模[11-12]
1.1 自忆性原理
设系统演化动态方程组可写为

式中J—整数;x—为第i个变量;λ—参数;r—空间;t—时间。
为简便计,下文只考虑单个变量x。设所讨论的变量和函数皆连续、可微、可积,定义记忆函数β(r,t)∈ H,β为r,t的函数 ,且|β(r,t)|≤1,在以下推导中固定在空间点ri上,故在β中省去r,在上式中省去i,在希尔伯特空间中定义内积

将式(2)定义的内积运算运用到式(1)上得
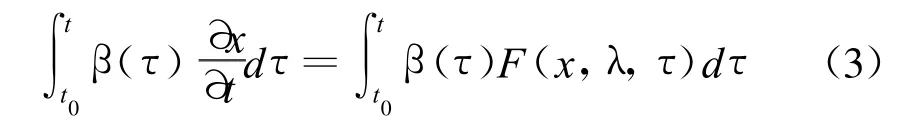
显然式(3)为对式(1)的一种加权积分,权重即为记忆函数。
运用分部积分及微分中值定理对式(3)进行变换和运算,并令,其余符合类推,可以得到

对于多个时次 ti,i=-p,-p+1,…,0,1,对式(1)进行积分并进行以上类似处理可得

这是一个差分-积分方程,称它为自忆性方程。令 p=0,则式(5)变为式(4),称式(4)为 0阶自忆性方程,式(5)为p阶自忆性方程。

由式(6)可知,在ri点的预报值在时次t的值由两项组成。只涉及到本空间点(即 ri点)的初始时次t-p和中间时刻的值,故称S1为自忆项;而S2为其他空间点对ri点在时间间隔[t-p,t] 中的总效应,故称为他效项。式(6)的物理意义是,第ri点在时次t的x值等于本点过去x值的自忆效应加上源函数F(x,λ,t)与记忆函数乘积的累计和。
1.2 自记忆方程的离散表达
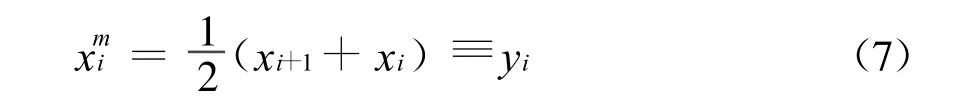
设时次为t,t0,t-1,…,t-p,取等距时次间隔,可令△ti=ti+1-ti=1。将 βt和βi合写,则得离散形式的自忆性方程

1.3 记忆系数的求解
正如只有很少量微分方程有解析解,自忆性方程也一样。因此只有用计算机求其数值解。用L个时次的历史资料,用最小二乘来求记忆系数 αi,θi,设空间共 N 个点 。记

可得矩阵方程为

令

则式(9)变为

其最小二乘解为

求出系数矩阵W后就可以对时间序列进行拟合和预测,最后还原为原始数据。
2 趋势曲线模型[13-15]
趋势曲线预测模型即假设数据变量大致沿某一趋势曲线变化,从而用曲线方程模拟这一变化,进而对未来数据进行预测。常用的为多项式趋势曲线。
假设多项式趋势曲线为

当函数的个数等于m+1时,能唯一解得所有的待定参数,当函数值的个数大于m+1时,按最小二乘法也能唯一解得所有的待定参数。待求得所有待定参数后可得到趋势曲线预测模型为^Yt=

3 趋势曲线-自记忆模型的建立
基于物理运动不可逆性提出的自记忆性原理,针对有微分方程描述的动力系统,可以建立相应的自记忆模型。但在很多情况下往往只有时间序列观测值,而没有现成的描写系统的微分方程。如果对一次累加(1-AGO)时间序列x(1)(i)求多项式趋势曲线为f(x)=a0+a1t++…+,一次累加生成序列x(1)(i)可视为函数f(x)在ti处的离散点,即X(1)(i)=a0+a1ti+对上式求微分既可得到系统动力微分方程以此式作为系统动力微分方程可以建立趋势曲线-自记忆组合预测模型。
4 工程实例
取某工程2009年6月13日到2009年9月26日监测数据,每隔三天取一个监测数据,见表1。
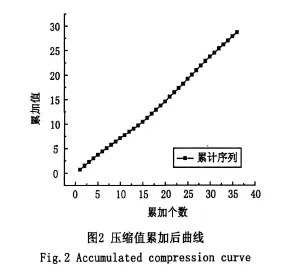
首先对表1中数据系列按除以最大值的方法进行压缩处理,使各数值均变换到0至1之间(图1),再对其进行一次累加生成(1-AGO),得X(1)(图2)。从图1和图2可以看出,原始序列X(0)为一波动较大的不规则时间序列,难以用解析函数拟合,而经过一次累加生成序列X(1)具有较明显曲线特性,可以对其进行趋势曲线拟合。
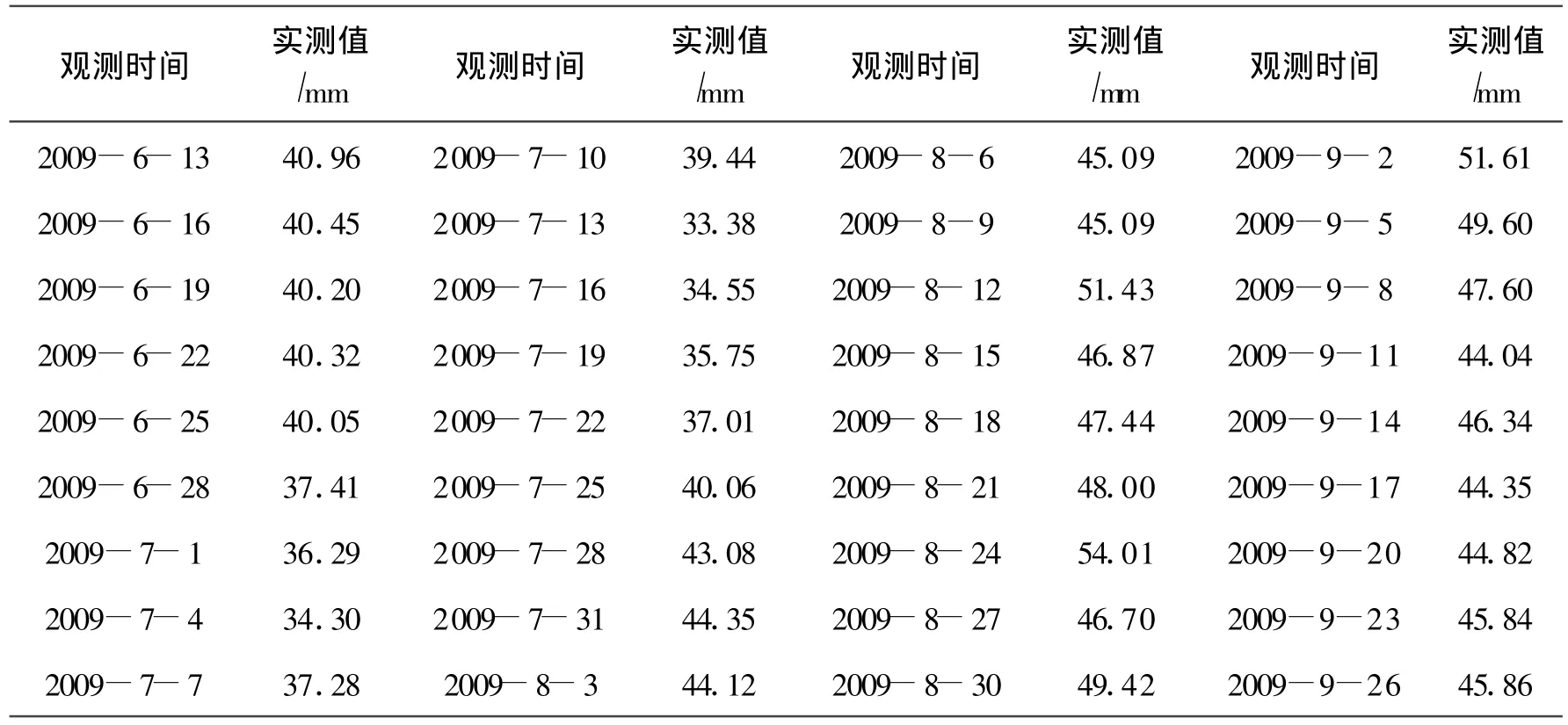
表1 监测点监测数据Tab.1 Monitoring data of one monitoring point

分别用上述建立的两种预测模型和灰色GM(1,1)模型对表1中2009年6月13日到2009年9月8日的位移监测数据进行拟合计算,并对2009年9月11日到2009年9月26日的监测数据进行预测检验。
4.1 灰色GM(1,1)模型

表2 灰色GM(1,1)模型预测值与监测值比较Tab.2 Comparison between monitoring values and predicted values
对X(1)拟合成一阶线性微分方程,并按最小二乘法求解,得最小二乘估计参数数列^a=(a,b)T=(-0.01317,0.64037)T。则时间响应函数为

再做累减生成,可得模型的还原拟合值
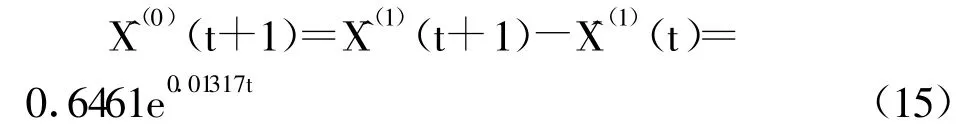
灰色GM(1,1)模型预测值与监测值比较见表2。
4.2 趋势曲线模型
在建立趋势曲线模型过程中,使用等维新息建模法[16],即采取增加新信息和去掉老信息同时进行的方式建模,使数列维数保持不变。如对X(1)建立模型预测x(1)(n+1)后,对X(1)进行等维新息处理后得到新数列X(1)=(x(1)(2),x(1)(3),…,x(1)(n),x(1)(n+1)),再用此数列建模预测x(1)(n+2),以此类推。趋势曲线预测值和监测值对比见表3。

表3 趋曲线预测模型预测值与监测值比较Tab.3 Comparison between monitoring values and predicted values of trend curve prediction model
4.3 趋势曲线-自记忆模型
建立趋势曲线-自记忆模型过程时,取回溯阶p=5(根据拟合情况通过试算法确定),在建模过程中同样采取等维信息建模方法,可获得位移预测方程为

用上述建立的自记忆模型对表1中2009年6月13日到2009年9月8日的位移监测数据进行拟合计算,并对2009年9月11日到2009年9月26日的监测数据进行预测检验。趋势曲线-自记忆模型预测值与监测值比较见表4。

表4 趋势曲线-自记忆模型预测值与监测值比较Tab.4 Comparison between monitoring values and predicted values of the trend curve-self-memory model
5 基坑位移预测对比分析
分析三种模型拟合和预测计算结果可知,使用GM(1,1)预测模型时,参与拟合计算的三十个样本拟合相对误差范围为0.39%~19.26%,平均相对误差为6.27%。预测计算结果中,相对误差范围为 13.3%~20.6%,平均相对误差为18.47%。使用趋势曲线预测模型时,拟合计算的相对误差范围为0.06%~9.99%,平均相对误差为3.23%。预测计算结果中,相对误差范围为1.9%~19.0%,平均相对误差为11.38%。使用趋势曲线-自记忆模型时,拟合计算的相对误差范围为0.01%~7.51%,平均相对误差为2.99%。预测计算结果中,相对误差范围为2.05%~18.01%,平均相对误差为8.9%。
6 结论
1)三种预测模型中,灰色GM(1,1)模型预测精度较低,趋势曲线模型相对较高,本文提出的趋势曲线-自记忆模型预测精度最高。
2)趋势曲线-自记忆模型利用多个历史资料提供的记忆信息,某个监测值出现一定误差对拟合和预测整体影响较小,提高了预测稳定性。
[1] 廖展宇,李英,晏鄂川,等.非等间隔时序灰色模型的深基坑变形预测研究[J] .合肥工业大学学报(自然科学版),2009,32(10):1521-1525.
[2] 庄妍,陈晓斌.GM(1,1)模型基坑结构变形预测应用研究[J] .广州建筑,2009,6(12):26-30.
[3] 李磊,姜志强.深基坑支护结构位移的非等步长灰色模型预测[J] .勘察科学技术,2001(5):16-19.
[4] 李祥新,俞进萍.锚杆围护结构的深基坑开挖中侧向位移的预测控制[J] .探矿工程,2002(4):3-6.
[5] 陈记,韦立德.RBF网络在基坑支护水平变形预测中的应用[J] .广西工学院学报,2005,16(1):12-15.
[6] 王旭东,赵建平,余闯,等.人工神经网络在深基坑变形预测中的应用[J] .南京工业大学学报,2002,24(5):73-76.
[7] 韦立德,徐卫亚,蒋中明,等.基坑支护结构水平变形预测的遗传神经网络方法[J] .工程地质学报,2003,11(3):297-301.
[8] 李云璋,韩晓雷.深基坑支护结构位移的神经网络预测[J] .水利与建筑工程学报,2006,4(4):22-25.
[9] 李爱国,袁宝远,陈艳国,等 .灰色神经网络在深基坑位移预测中的应用[J] .人民黄河(水利水电工程),2006,28(4):77-79.
[10] 李荣峰.地下水动态预测的自记忆性模型及其应用研究[J] .山西水利科技,2005(1):6-8.
[11h曹鸿兴.动力系统自忆性原理─预报和计算应用[M] .北京:地质出版社,2002.
[12] 李荣峰.水文非线性时间序列分析的自记忆模型研究[D] .西安:西安理工大学,2005.
[13] 左秀霞,王 伟,张伟苇.多项式趋势曲线预测模型及软件设计[J] .长江大学学报(自然科学版),2004,1(1):10-13.
[14] 李均立.GM(1,1)模型与趋势曲线的组合预测方法在橡胶产量预测中的应用[J] .热带农业科学,1997,2(2):9-13.
[15] 谢成立,刘磊.灰色-趋势曲线组合预测模型在港口吞吐量预测中的应用[J] .中国水运,2006,6(12):226-227.
[16] 易德生,郭 萍.灰色理论与方法[M] .北京:石油工业出版社,1992.

