FRP-混凝土界面黏结-滑移关系反演分析

冯新权,刘鹏飞,陈 瑛

(1.山东省水利勘测设计院,山东济南 250013;2.山东恒信建筑设计有限公司,山东济南 250100;3.山东大学土木工程系,山东 济南 250061)

掌握单剪FRP板-混凝土试件界面的黏结应力-滑移(τ-δ)关系有助于分析单剪FRP板-混凝土试件的脱黏机理[1-3].单剪试验是研究单剪FRP板-混凝土试件界面剪切黏结性质的常用方法[4-6].为了获得τ-δ关系,通常在FRP板上粘贴应变片.目前文献中有很多种τ-δ的关系[7-11],造成试验结果差异的主要原因在于:单剪FRP板-混凝土试件有效黏结长度很小,难以放置足量的应变片;局部变形大,在FRP板表面观察到的应变值离散性很大;黏结应力具有非线性.单剪FRP板-混凝土试件剪切试验表明[1],剪切破坏多发生于与胶结层相黏的几毫米范围内的界面混凝土上,因此,单剪FRP板-混凝土试件界面应包括胶结层和界面混凝土,仅测量FRP板的变形是不正确的.

为了解决以上问题,本文采用反演分析法确定单剪FRP板-混凝土试件的 τ-δ关系.该法无需测量FRP板拉拔过程中整个界面的黏结应力-滑移关系,而是根据拔出力和加载点处测量的FRP板-混凝土的相对剪切滑移确定.

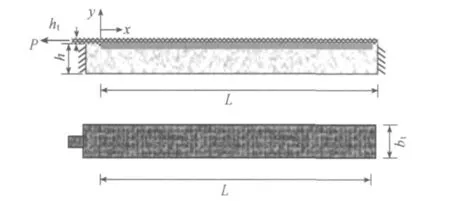
图1 FRP板-混凝土单剪试件模型Fig.1 Simple shear specimens of FRP sheet-concrete

1 控制方程

图1为单剪FRP板-混凝土试件,黏结长度为L.FRP板和混凝土的高度分别为ht和 h,胶结层厚度为ta,拉力为P.图2为试件的一段微小的隔离体d x,τ(x)为界面剪应力.式中Ni(x)和Mi(x)(i=b,t分别代表混凝土和FRP板)分别为混凝土、FRP板的轴力和弯矩,M T,N T为总的弯矩和轴力,b t为FRP板和混凝土宽度.

假定胶结层内剪应力和正应力沿厚度方向分布均匀,由图2可得界面上任意点的水平变形δ(x)为

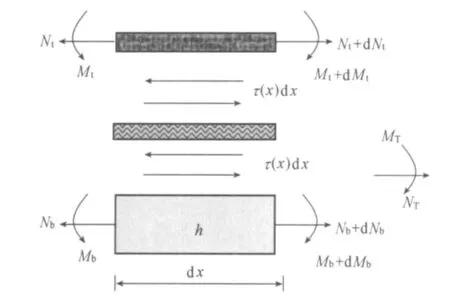
图2 FRP板-混凝土单剪试件隔离体Fig.2 Free bodies for simple shear specimens of FRP sheet-concrete

式中u,w为纵向(x向)和横向位移(y向).

对式(1)求导,并结合Euler-Bernoulli梁理论,得

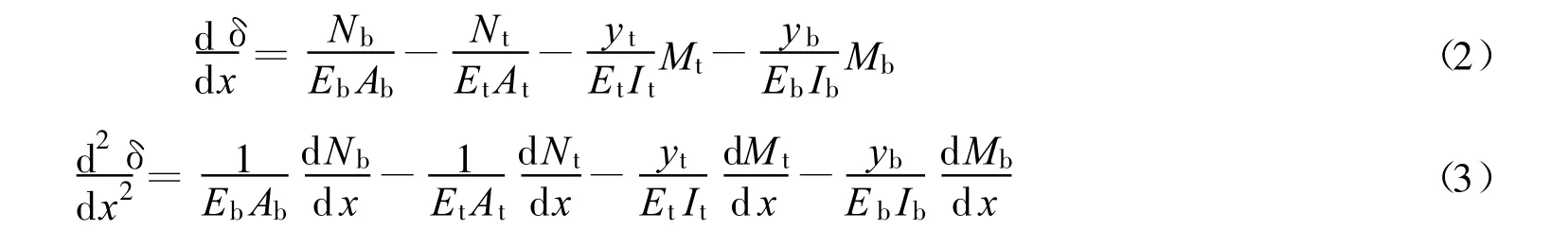
式中:E——弹性模量;G——剪切模量;A——横截面积;I——截面惯性矩;y t,y b——FRP板底部和混凝土顶部距各自截面形心的距离.

根据轴向的平衡条件:

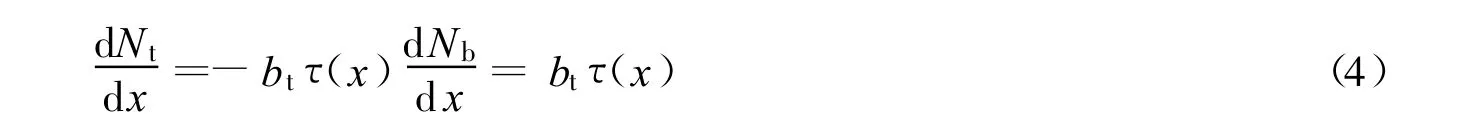
根据弯矩平衡条件:

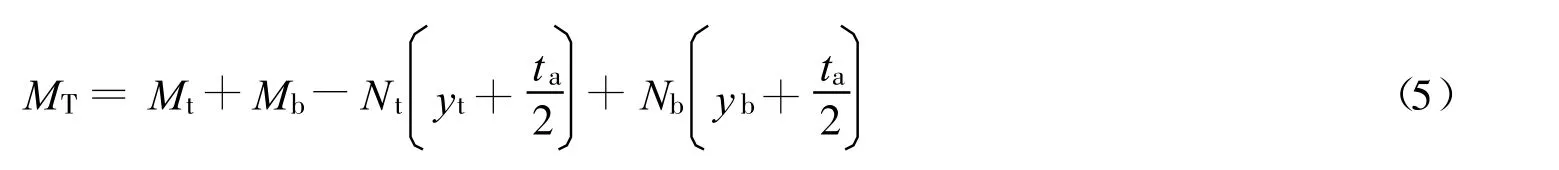
对式(5)微分得

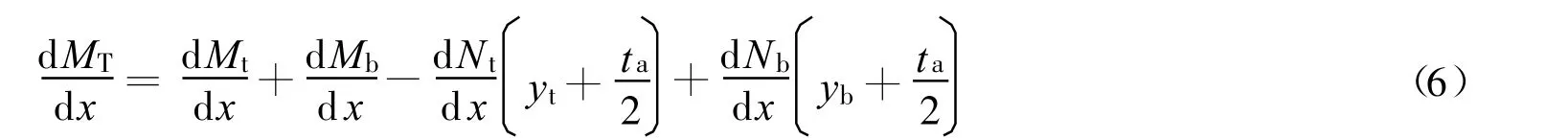
假定混凝土和FRP板曲率相等,则有

将式(4),(5),(7)代入式(6)得

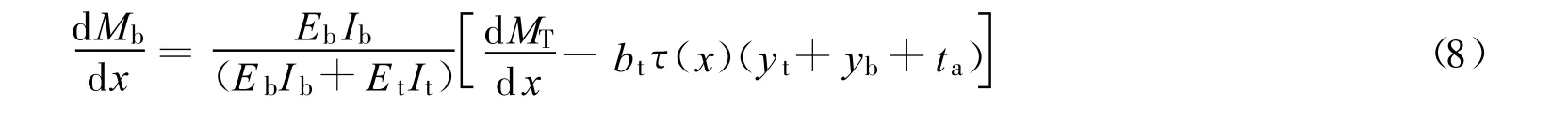
因为:

将式(4),(5),(8),(9)代入式(3)得:

其中:

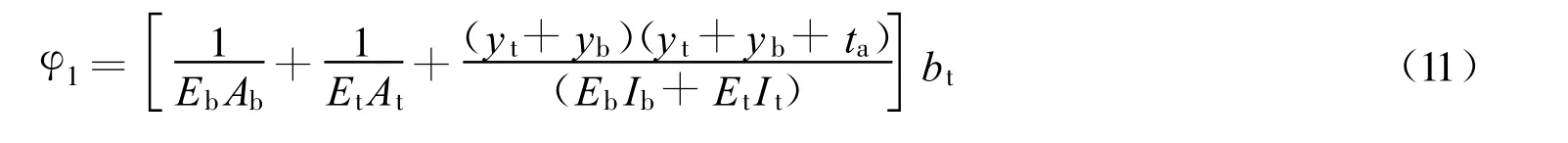
2 黏结应力-滑移反演公式

当试件足够长,边界条件为:

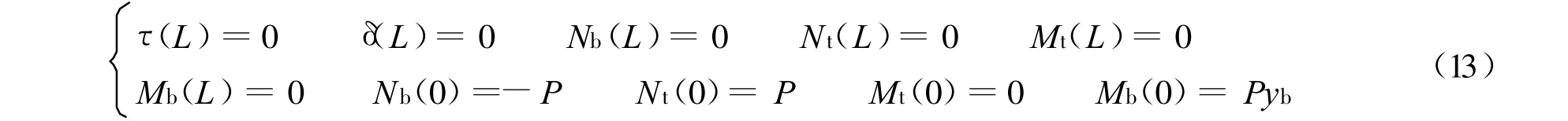
将边界条件式(13)代入式(2)得

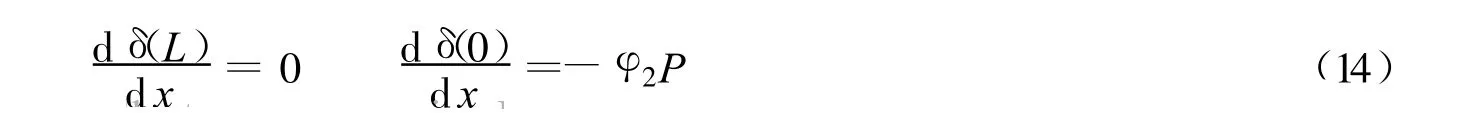
其中

将式(14)代入式(12)得

根据式(16),函数 P(δ(0))由函数 τ(δ(0))唯一确定,反之界面本构关系 τ(δ(0))也可由 P(δ(0))确定.式(16)对 δ(0)微分可得

因此,根据测得的荷载P和剪切变形δ(0)可确定黏聚法则.

能量释放率为

由于 τ(δ)≥0,式(18)表明 δ(0)随着荷载 P单调递增,反之亦然.故可得到稳定的试验数据.

若黏结应力-滑移关系为已知,根据式(17),可得到剪切变形与荷载P的关系.根据双线性黏结应力-滑移关系[4](图3),可得

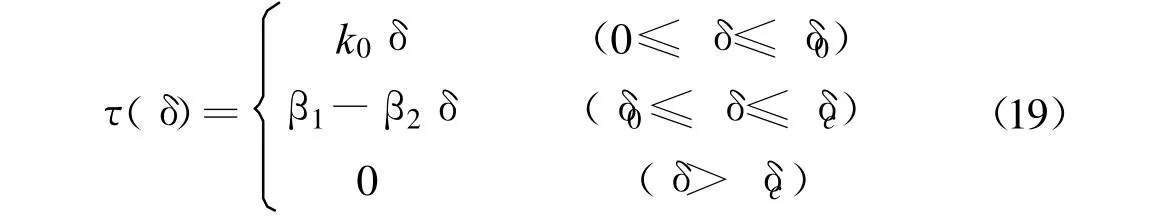
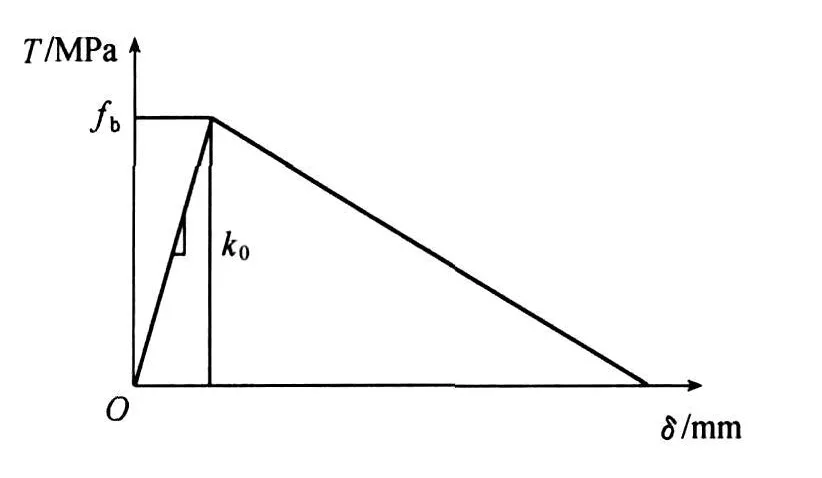
图3 黏结应力-滑移关系Fig.3 Bond-slip relationship

其中:

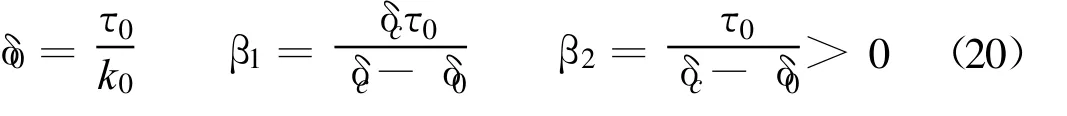
a.弹性阶段(0≤δ≤δ0):

由式(18),(21)得:

b.弹性-软化阶段(δ0＜δ≤δc):当 x=0时

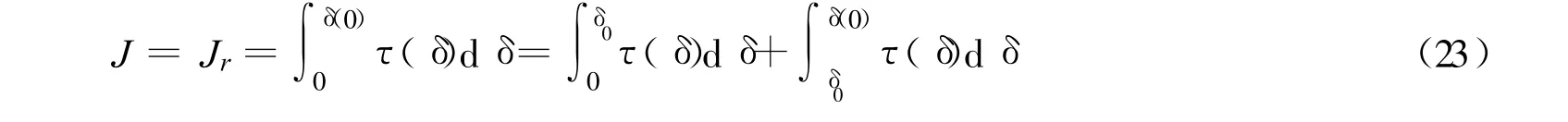
故:

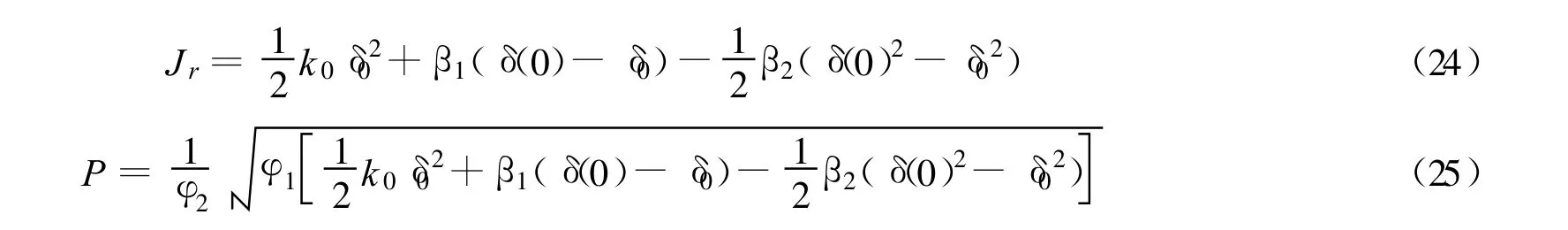
3 黏结应力沿界面的分布

虽然黏结应力沿界面的分布与非线性边值条件有关,但如果已知黏结应力-滑移关系,仍然可以确定黏结应力沿界面的分布.

式(27)表达了局部剪切变形与单位长度界面应变能的关系.

将式(27)变量分离,并从加载点到任意点x积分得:

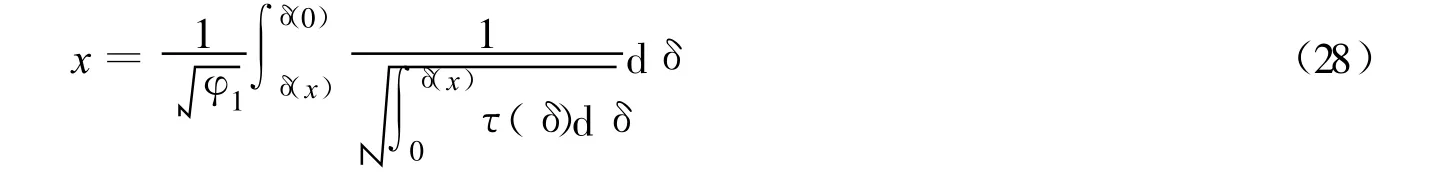
4 有限元分析

为验证反演的正确性,本文对CFRP(carbon fiber reinforced plastics)-混凝土单剪试件进行了有限元分析.试件的材料参数和尺寸如下:混凝土梁截面尺寸bt×h=100mm×50mm,L=450mm.通过环氧树脂胶结剂将碳纤维布、混凝土梁黏结在一起.碳纤维布厚度为0.1651mm.材料弹性模量E、剪切模量G和泊松比v见表1.表中1,3方向分别与图1所示的x,y方向重合,且1方向与碳纤维轴线方向平行.

表1 材料参数Table1 Parameters for materials

数值模拟用通用有限元程序ABAQUS 6.5,采用平面应力模型,混凝土、CFRP采用四边形八节点单元和三角形六节点单元,FRP板-混凝土界面布置一层双线形黏聚单元,黏聚模型的参数来自断裂试验[12].黏聚单元与混凝土和FRP板实体单元共用节点,因此,黏聚单元的损伤过程与主体材料的变形相耦合.图4为CFRP-混凝土4ENF界面剪应力分布随荷载增加的变化情况.黏聚模型的理论分析和有限元分析均能反映CFRP-混凝土单剪试件界面破坏经历弹性阶段、弹性-软化阶段、弹性-软化-脱黏阶段的逐渐发展过程.解析解与有限元结果非常接近,说明本文采用的反演法确定单剪FRP板-混凝土试件的τ-δ关系的正确性.

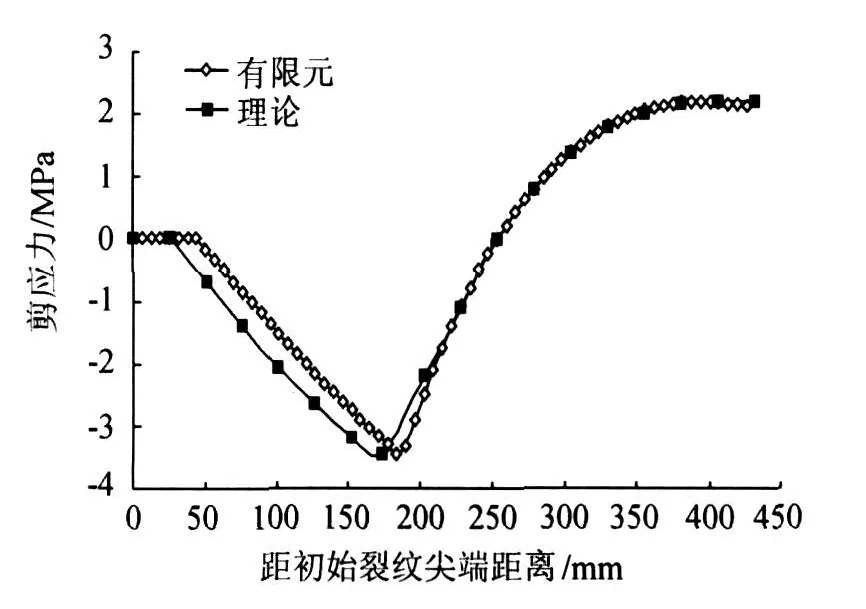
图4 界面剪应力分布有限元与理论分析结果对比Fig.4 Comparison of interfacial shear stresses between FEM analysis and theoretical prediction

5 结 语

本文采用反演分析法确定FRP板-混凝土单剪试件界面的黏结-滑移关系.该法无需测量FRP板拉拔过程整个界面的黏结应力-滑移关系,而是根据拔出力和裂纹嘴处测量的FRP板-混凝土的相对剪切滑移确定.

为了验证该模型的正确性,本文对FRP板-混凝土单剪试件进行了有限元分析.有限元分析与理论分析结果对照表明,反演分析法能精确预测界面的黏结应力-滑移关系.该模型不但适用于单剪FRP板-混凝土材料,还适用于类似其他双材料单剪试件界面的研究.

[1]陈瑛,乔丕忠.CFRP-混凝土界面4ENF断裂试验研究[J].河海大学学报:自然科学版,2009,37(1):96-99.(CHENYing,QIAO Pi-zhong.Fracture tests on CFRP-4ENF interfaces[J].Journal of Hohai University:Natural Science,2009,37(1):96-99.(in Chinese))

[2]陈瑛,乔丕忠,姜弘道,等.多亚层柔性节点模型及其在4ENF双材料界面断裂研究中的应用[J].计算力学学报,2008,25(6):821-826.(CHEN Ying,QIAO Pi-zhong,JIANG Hong-dao,et al.Multi-layer flexible joint model and its application to 4ENF specimen analysis of bi-material interface[J].Chinese Journal of Computational Mechanics,2008,25(6):821-826.(in Chinese))

[3]QIAO Pi-zhong,CHEN Ying.Cohesive fracture simulation and failure modes of FRP-concrete bonded interfaces[J].Theoretical andApplied Fracture Mechanics,2008,49(2):213-225.(in Chinese))

[4]陈瑛,乔丕忠,姜弘道,等.双材料断裂力学模型与实验方法[J].力学进展,2008,38(1):54-61.(CHEN Ying,QIAO Pi-zhong,JIANG Hong-dao,et al.Review on experimental methods and fracture models for bi-material interfaces[J].Advances in Mechanics,2008,38(1):54-61.(in Chinese))

[5]CHAJESM J,FINCH JRWW,JANUSZKA TF,et al.Bond and force transfer of compositematerial plates bonded to concrete[J].ACI Struct J,1996,93(2):208-217.

[6]YAO J,TENG JG,CHEN JF.Experimental study on FRP-to-concretebonded joints[J].Composites-Part B:Engineering,2005,36(2):99-113.

[7]MONG B O,ABDELDJELIL B,SANG W B.Effectivebond length of FRP sheets externally bonded to concrete[J].International Journal of Concrete Structures and Materials,2009,3(2):127-131.

[8]LU XZ,TENG JG,YEL P,et al.Bond—slip models for FRP sheets/plates bonded to concrete[J].Engineering Structures,2005,27:920-937.

[9]CHEN J F,TENG J G.Anchorage strength models for FRP and steel plates bonded to concrete[J].ASCE Journal of Structural Engineering,2001,127(7):784-791.

[10]UEDA T,DAI Jian-guo.Interface bond between FRP sheets and concrete substrates:properties,numerical modeling and roles in member behavior[J].Prog Struct Engng Mater,2005,7:27-43.

[11]陈瑛,乔丕忠.4ENF黏聚解析模型[J].河海大学学报:自然科学版,2008,36(2):234-237.(CHEN Ying,QIAO Pi-zhong.Cohesive analytic model of 4ENF specimen[J].Journal of Hohai University:Natural Science,2008,36(2):234-237.(in Chinese))

[12]陈瑛.双材料梁界面力学及其在FRP-混凝土界面断裂研究中的应用[D].南京:河海大学,2006.