非等间距GM(1,1)模型的改进及预测分析
梅 红,孙泽信
(河海大学地球科学与工程学院,江苏南京 210098)
坝堤的变形分析与预测,在坝堤的建设和使用过程中极为重要.目前针对这类问题的研究理论和方法都很多,在沉降变形的小样本监测离散数列方面,灰色GM(1,1)模型以其特有的优势得到了很好的应用.灰色GM(1,1)模型对数据的处理,不是求得数据的概率分布和统计规律,而是根据数据的处理方法找出数据间的规律,因而只需较少的数据[1-2].大量文献表明,灰色GM(1,1)存在一些预测精度不高的情况,因此,对灰色GM(1,1)模型进行深入的研究,找出影响模型精度的关键性因素并进行改进,提高灰色GM(1,1)预测模型的精度,具有非常重要的理论意义和实际价值.
本文从非等间距GM(1,1)模型的基本原理出发,在对模型精度的主要影响因素进行分析的基础上,对模型初值选取以及背景值的构造2个方面进行改进,最后结合某坝堤沉降监测实例进行预测分析.
1 非等间距GM(1,1)模型的建模过程
传统的灰色GM(1,1)模型是以等间隔数列为基础的,但在实际工程的变形监测中,观测数据的时间间隔往往呈现非等间隔的状态,这就限制了传统灰色GM(1,1)模型的应用.这时,需要把非等时间间隔转化为等时间间隔序列.本文主要采用单位时段差系数修正法对原数据进行处理,再进行一次累加生成处理,进而形成非等间距GM(1,1)模型[3-5].
设X(0)={x(0)(ti)i=1,2,…,n},ti∈R,ti与ti+1之间为任意非等间距,即 Δti=ti+1-ti不为常数.则平均时间间隔Δt0为

单位时间差系数 μ(ti)为

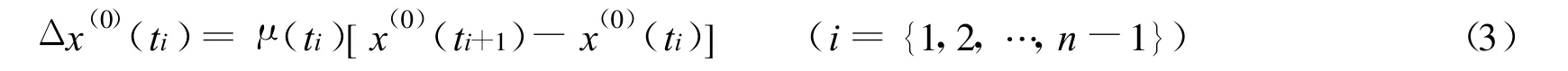

于是得到等间隔序列为

将x(1)1(t)拟合成一阶线性微分方程,即

式中:a,u为待定常数.a称为发展系数,其大小反映了序列 x(0)的增长速度;u称为灰色作用量.则可得到方程组:

其中

其法方程组为

则最小二乘解为

得到时间响应函数为
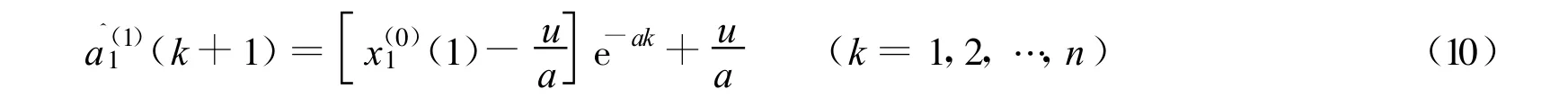
还原为非等间距数列中与时间t有关的函数(t为距首次周期的时间间隔)为

则
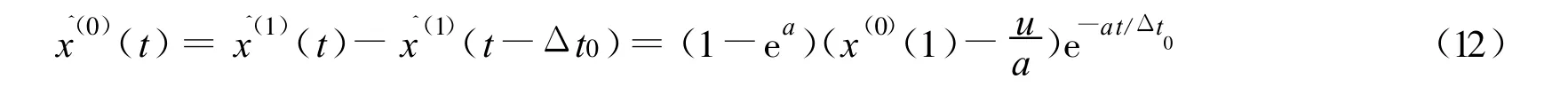
将预测时间t代入式(12),即可求得预测值.
2 非等间距GM(1,1)模型精度检验
建模的主要目的在于预测.为了评价预测的精度和效果,有必要对所建模型精度进行检验.灰色模型的精度通常采用后验差方法检验,其基本过程如下[6]:
a.计算残差.记k 时刻 x(0)(k)与(0)(k)之差为

b.计算原始数列和残差数列的方差:

其中

c.计算后验差比值C和小误差概率p:

d.模型精度评定.指标C越小越好,C越小,表示S1越大而S2越小.S1大,表示原始数据离散程度大;S2小,表示残差离散程度小.指标p越大越好,p越大,表明残差与残差平均值之差小于给定值0.6745S1的数据比较多.根据C与p 2个指标,可综合评定模型精度.模型精度评定标准如表1所示.
3 非等间距GM(1,1)模型精度影响因素分析
由非等间距GM(1,1)模型的建立过程及其基本原理可知,影响该模型预测精度的因素主要有以下几个方面:(a)原始数据的选取.构成非等间距GM(1,1)模型的原始数据必须在正常的类似条件下得到,否则拟合所得的模型不具有较强的规律性.(b)初值的选取.在传统的GM(1,1)预测模型中,取 x(0)(1)作为初值显然不太合理,因为模型的最佳拟合曲线有可能不通过 x(1)序列中任何一个数据[7-8].(c)模型背景值的构造.传统的灰色GM(1,1)预测模型是基于对积分函数的近似,与实际情况不符.(d)非等间距GM(1,1)模型是一指数模型,它反映的是变形体单纯随时效的变化情况.如果有其他外界因素对变形或沉降产生较大影响,如荷载的突然变化,则会大大影响所建模型的精度[9-10].(e)数据维数的影响.灰色模型针对不同的实际情况,存在着不同的最佳维数,只有选择了合适的维数,才可以使模型精度达到最佳[11-12].

表1 模型精度评定标准Table 1 Assessment criteria for model precision
4 非等间距GM(1,1)模型的改进
4.1 初值的改进
在传统的灰色GM(1,1)模型中,取x(0)(1)作为初值.但是由于模型的最佳拟合曲线有可能不通过 x(1)序列中任何一个数据,因此,x(0)(1)作为初值并不合理,故须对其改进.若要提高模型的精度,必须使残差数列的方差最小,故本文利用最小二乘法对初值进行改进.即使达到最小.

求解方程


其中
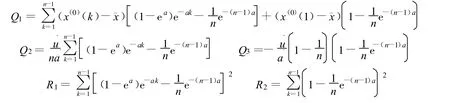
4.2 背景值构造的改进
由式(6)可得

其中
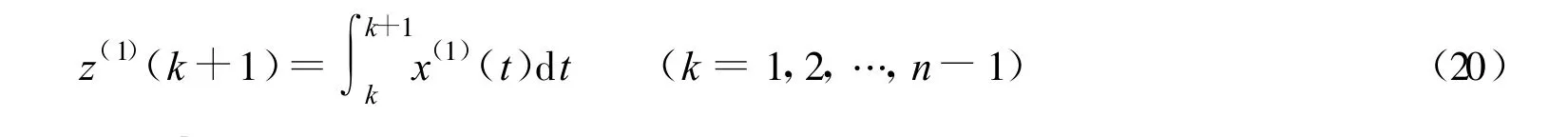
称为模型背景值.但在传统的灰色GM(1,1)模型中,其背景值的构造采用
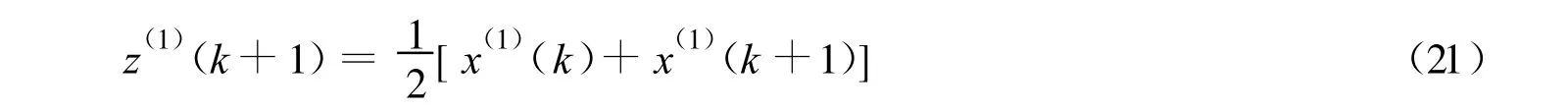
从式(20)可以看出背景值z(1)(k+1)是x(1)(t)在区间(k,k+1)上的定积分,而传统的背景值实际上是该定积分的近似算法,把x(1)(t)近似成一条直线.近似公式的误差有可能很大,导致模型预测的精度较低.因此,在其他条件不变的情况下,若要提高模型的预测精度,只有尽可能减少模型中背景值的计算误差.
从非等间距GM(1,1)模型的求解结果来看,可设

式中 m,p,q为3个独立的未知数.由此可知,每3个相邻的 x(1)(t)即可确定一个(1)(t)函数,即(1)(k),x(1)(k+1),x(1)(k+2)确定(1)(k+1),这样就可以把整个 x(1)(t)拟合成 n-1个独立的指数函数.这将大大减少背景值构造计算误差,从而提高模型的预测精度.
则背景值计算公式为

其中
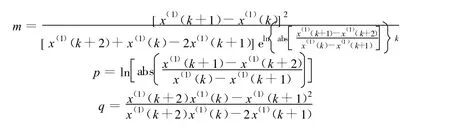
5 实例分析
某坝堤位于地质条件很差的软土地区,需要在坝堤全部施工阶段进行沉降观测,并通过变形分析和预报调节施工速度,以保证坝堤的施工安全.表2为坝堤某一沉降监测点的部分观测数据.
按照本文改进方法进行建模,并用改进的非等间距GM(1,1)模型对沉降进行预测分析.所建模型精度与改进前模型比较结果如表3所示.对模型进行不同的改进,改进后模型的精度等级如表4所示,沉降预测结果如表5所示.
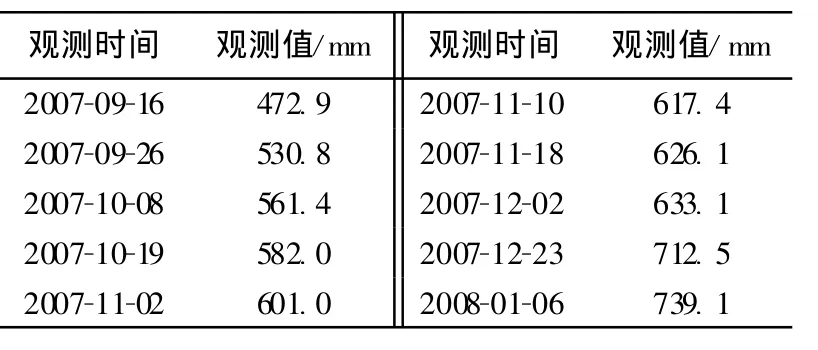
表2 沉降观测数据Table 2 Observed data of settlement

表3 模型精度比较Table3 Comparative results of model precision
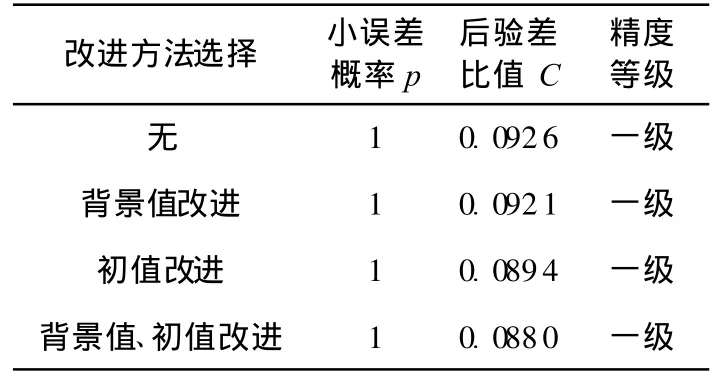
表4 模型的改进与精度等级Table4 Improvement and accuracy grade of model
从表3可以看出,非等间距GM(1,1)模型改进后拟合值与实测值更加接近,改进前平均相对误差为1.04%,改进后平均相对误差为0.76%,模型的拟合精度有较大提高;从表4可以看出,所建的非等间距GM(1,1)模型的精度等级为一级,对模型进行改进后,后验差比值C变小,表明模型的改进是有效的;从表5预测结果来看,预测值和实测值相当接近,改进前预测值的最大相对误差为5.61%,最小相对误差为0.73%,平均相对误差为2.40%,改进后预测值的最大相对误差为2.76%,最小相对误差为0.34%,平均相对误差为1.07%,表明改进后的非等间距GM(1,1)模型可靠性更强,精度更高.
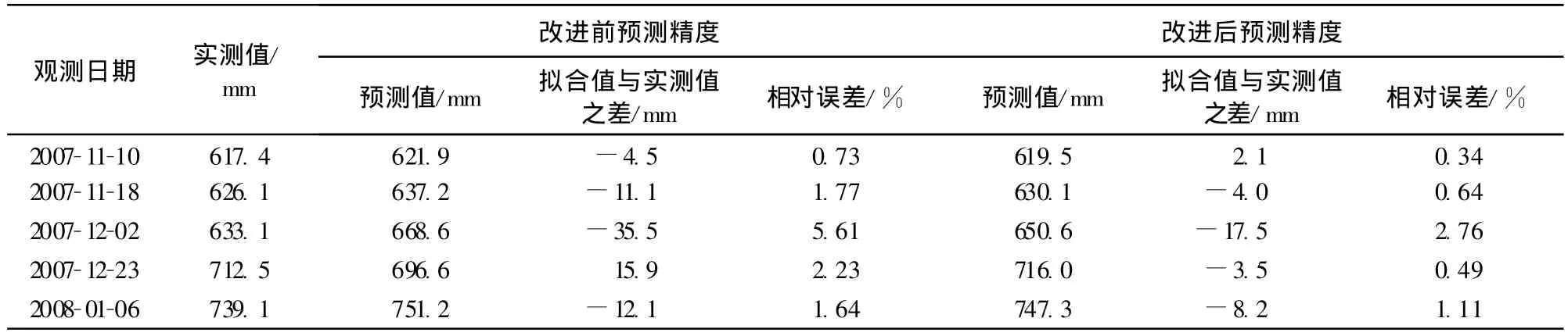
表5 沉降预测结果Table5 Results of predicted settlement
6 结 论
a.从根据某坝堤沉降监测的5组数据所建模型的精度等级来看,非等间距GM(1,1)模型比较适合小样本离散数据的处理,利用很少数据即可进行较为准确的预测分析.
b.对某坝堤沉降的预测分析结果表明:非等间距GM(1,1)模型初值的选取及背景值的构造方法,都是影响GM(1,1)模型预测精度的重要因素;改进后模型的预测精度有了更大的提高.
c.运用改进后的非等间距GM(1,1)模型对后续5个观测时间的累积沉降量进行了预测,预测值较模型改进前与实测值更加接近,表明改进后的模型可靠性更强,精度更高,更适用于坝堤的沉降预测分析.
[1]邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.
[2]XIE Nai-ming,LIU Si-feng.Research on discretegrey model and its mechanism[C]//Systems,Man and Cybernetics,2005Proceedingof the IEEE International Conference.Piscataway:IEEE Xplore Digital Library,2005:606-610.
[3]黄声享,李志成.工程建筑沉降预测的非等间距灰色建模[J].地理空间信息,2004,2(1):41-43.(HUANGSheng-xiang,LIZhicheng.Grey modeling of non-equidistant data sepuent for forecasting subsidence of the engineering buildings[J].Geospatial Information,2004,2(1):41-43.(in Chinese))
[4]谢乃明,刘思峰.离散GM(1,1)模型与灰色预测模型建模机理[J].系统工程理论与实践,2005,25(1):93-99.(XIE Nai-ming,LIUSi-feng.Discrete GM(1,1)and mechanism of grey forecasting model[J].Systems Engineering-Theory&Practice,2005,25(1):93-99.(in Chinese))
[5]郭丽萍,孙伟,郑克仁,等.非等时距GM(1,1)直接模型及其在材料试验数据处理中的应用[J].东南大学学报:自然科学版,2004,34(6):833-837.(GUO Li-ping,SUN Wei,ZHENG Ke-ren,et al.Non-equal interval GM(1,1)direct model and its application in processing of materials experimental data[J].Journal of Southeast University:Natural Science Edition,2004,34(6):833-837.(in Chinese))
[6]袁嘉祖.灰色系统理论及其应用[M].北京:科学出版社,1991.
[7]张大海,江世芳,史开泉.灰色预测公式的理论缺陷及改进[J].系统工程理论与实践,2002,22(8):140-142.(ZHANGDa-hai,JIANGShi-fang,SHI Kai-quan.Theoretical defect of grey prediction formula and its improvement[J].Systems Engineering-Theory&Practice,2002,22(8):140-142.(in Chinese))
[8]唐万梅.几个预测方法及模型的研究[D].呼和浩特:内蒙古大学,2006.
[9]谭冠军.GM(1,1)模型的背景值构造方法和应用[J].系统工程理论与实践,2000,20(4):98-103.(TAN Guan-jun.The structure method and application of background valuein grey system GM(1,1)model[J].Systems Engineering-Theory&Practice,2000,20(4):98-103.(in Chinese))
[10]WANG Z G,WU C D.The establishment and application of an improved GM(1,1)model[J].Mathematics in Practice and Theory,2003,33(9):20-25.
[11]朱华吉,马少娟.非等时空距GM(1,1)模型在建筑物沉降预测中的应用[J].测绘工程,2001,10(4):39-41.(ZHU Hua-ji,MA Shao-juan.Application of non-equal interval gray model to forecast of building subsidence[J].Engineering of Surveying and Mapping,2001,10(4):39-41.
[12]HUANG Y P.The identificationof fuzzy grey prediction system by genetic algorithm[J].International Journal of System Science,1999,29(4):547-588.

