Rayleigh-Ritz法在应用中需注意的几个问题

彭 震,贾培强,李 晶

(唐山学院,河北唐山 063000)

Rayleigh-Ritz法在应用中需注意的几个问题

彭 震,贾培强,李 晶

(唐山学院,河北唐山 063000)

结合实例提出了Rayleigh-Ritz法在应用中需注意的几个问题,有助于Rayleigh-Ritz法的准确运用,从而提高利用该方法解决问题的计算精度。

Rayleigh-Ritz法;试函数;边界条件;势能泛函;完备性

Rayleigh-Ritz法[1]是用最小势能原理推导出的一种计算方法,在结构分析中的重要应用之一是利用它求解复杂问题的近似解。当Rayleigh-Ritz法在1908年被提出时,其理论基础并不完备,只是在实践中证明它卓有成效。它的理论基础在经过人们多年努力后才开始有了头绪。由于教材对此问题阐述的不多,在用其求解收敛性问题时又涉及到较深的泛函分析,故本文仅从该方法应用的角度做些探讨。

1 Rayleigh-Ritz法的本质

Rayleigh-Ritz法解决问题的出发点是将弹性结构的总势能 П表达成结构位移的函数。对于一个处于稳定平衡条件下的弹性结构,依据最小势能原理,使结构总势能 П取得最小值的位移就是真实位移。位移试函数可预先假设为无穷级数、富里叶级数或任何其它形式的级数。

例如,将试函数设为无穷级数

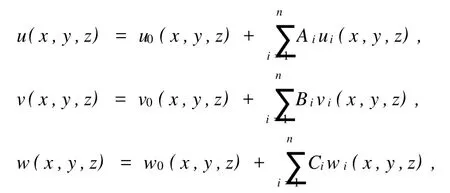
式中 u0,v0,w0,ui,vi,wi为满足边界条件的假定位移函数, Ai,Bi,Ci为任意常数。

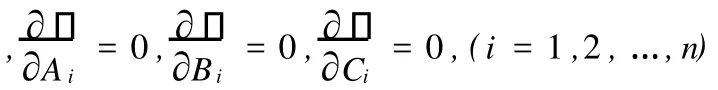
对于实际问题而言,由于结构的复杂性,事先假定的位移函数只能近似地表示结构的真实变形形状,基于近似形状,利用位移函数的微分,可求反力和应力合力的近似值。由于反力和应力合力也是近似的,它们就不可能与结构上的实际载荷形成静力平衡。可见Rayleigh-Ritz法的本质是在维数降低后的解空间去寻找近似解。

这里需强调一点,称 Rayleigh-Ritz法是一种近似解法(一些书籍中的称谓),和用它求近似解是不同的。可以肯定的是,若能列出包含真实位移在内的所有位移,该方法亦可求得精确解。

2 多项式的项数对试函数的影响

将试函数写成无穷级数的形式,泛函将由无穷数列 a1, a2,…,an,…来确定。根据Weierstrass定理,若试函数符合连续函数的要求,可以靠增加项数来提高精度。由于一般情况需联立求解方程才能得出系数 ai,数值条件不利于求解,所以,试函数在形式上是依赖于有限个参数an的函数族。

3 两类边界条件对试函数的影响

使用Rayleigh-Ritz法能否获得成效,很大程度上与假设的位移函数 ——试函数选取是否得当有密切关系。构造位移试函数最好满足两类边界条件:一类是试函数须事先满足的几何边界条件;另一类是由势能泛函驻值要求导出的条件,变分学称之为强制边界条件和自然边界条件[2]。

3.1 强制边界条件的影响

强制边界条件由对实际约束情况的分析给定。如图1所示的四边简支矩形薄板,其上有垂直于板面的任意分布荷载作用。位移试函数可假设为双重正弦级数

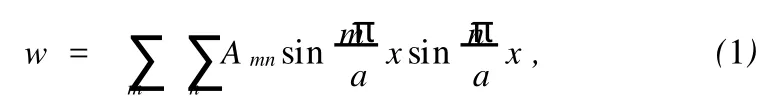
满足w为垂直板面方向的位移的几何边界条件是x=0,x= a处,w=0;y=0,y=b处,w=0。

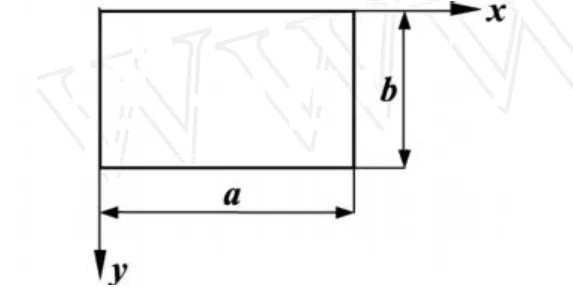
图1 四边简支矩形薄板

进一步分析还可知,在简支边处,限制自由翘曲,而允许绕着边界的缘线自由转动,故x=0,x=a处,绕x轴的弯矩Mx=0;y=0,y=b处,绕y轴的弯矩My=0。由弹性力学可知,将弯矩用位移试函数表示,上述条件也是满足的。可见试函数的完备性越好,就越接近真实的位移函数。能否将问题考虑得面面俱到,就目前而言还靠经验和深入分析。

又如图2所示等截面悬臂梁,试函数可写成n次多项式

也可写成三角级数式

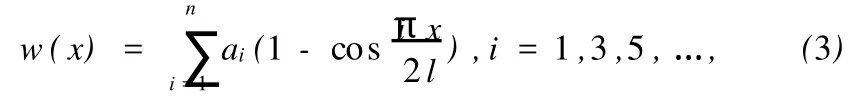
上两式均满足位移边界条件x=0处,w=0;x=l处,w≠0。

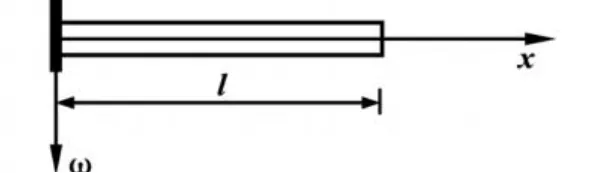
图2 等截面悬臂梁

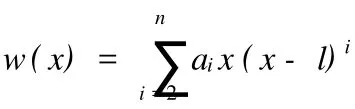
3.2 自然边界条件的影响

选择试函数满足自然边界条件是不容易做到的。现用下例说明自然边界条件。图3所示一端固定一端自由的等截面直杆,受轴向载荷q(x)=x作用,设 EA=1,l=1,用试函数u(x)=a1x+a2x2来表示杆沿轴线方向位移,势能泛函可写成

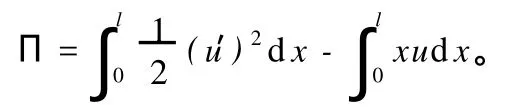
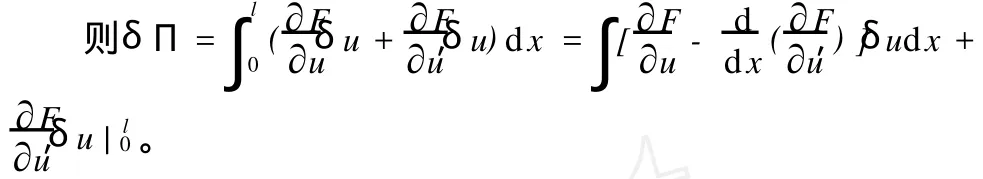
按驻值要求δП=0导出,在 x=0处,有δu=0为强制

图3 受轴向载荷的一端固定一端自由的等截面直杆

4 完备性对试函数的影响

Rayleigh-Ritz法是将含有无限多变量的泛函变分问题转换成有限个多变量的函数极值问题来处理的一种方法。若试函数满足边界条件,且泛函的积分表达式的积分值接近泛函的极小值,则可认定这样构造的函数序列将收敛于问题的解。

考察完备性是指假设的位移函数的近似程度是否真实准确地反映了结构的变形。构造满足整个定义域所有边界条件的试函数是困难的,通常可采用一些现有的结论。如泛函本身有二阶导数项,选取的试函数就应使二阶导数存在,等等。总之,对事物认识得越透彻越全面,越利于提高解的精度。有限单元法是Rayleigh-Ritz法局部化的解法,其核心是将解域离散,使每个单元具有完备性较好的试函数,然后再在一定条件下进行总装。这种方法能适应各种复杂形状,现已成为行之有效的工程分析手段。

[1] 孙训方,方孝淑,关来泰.材料力学[M].北京:高等教育出版社,1994:249.

[2] 胡海昌,胡润莓.变分法[M].北京:中国建筑工业出版社,1987:14.

(责任编校:夏玉玲)

Questions in the Application of Rayleigh-Ritz Method

PENG Zhen,JIA Pei-qiang,LIJing
(Tangshan College,Tangshan 063000,China)

Combined with examples,several questions w ere pointed out in the apllication of Ray-leigh-Ritz method.Solving these problems can contribute to the right apllication of Rayleigh-Ritz method and also imp rove the calculation accuracy.

Rayleigh-Ritz method;trial function;boundary condition;potential energy fonctio-nelle;completeness

O177

A

1672-349X(2010)06-0008-02

2010-07-14

彭震(1955-),男,教授,主要从事固体力学的教学与研究。