马尔可夫链理论在风险型决策问题中的应用

李 钢，黄祖光

（1.河北工业大学 管理学院，天津 300130；2.石家庄铁道大学 后勤处，河北 石家庄 050043）

一、引言

决策问题可以分为确定型决策，严格不确定型决策和风险型决策[1]。确定型决策问题的特点是决策人在进行选择之前了解真实自然状态，即可以确切地知道各种行动的后果，这类问题的求解纯属运筹学中的纯量优化问题。严格不确定型问题是指决策人只能知道有哪些自然状态可能出现，而无法以任何方式量化这种不确定性，也就是说各种自然状态出现的概率无法估计。风险型决策问题中，决策人虽然无法确知将来的真实自然状态，但他不仅能给出各种可能出现的自然状态，还可以给出各种状态出现的概率，通过设定概率来量化不确定性。求解随机问题的基础是得到自然状态的概率分布，得到这些概率的方法是根据过去发生的情况和有关统计资料进行推算，得出各种自然状态出现的概率。

由于种种原因，设定比较准确的状态概率分布是很困难的事。一般情况下，决策分析的结果往往对状态的概率分布比较敏感，即自然状态概率分布大小的变化会显著地改变分析结果，因此要提高决策分析的精度就必须设法提高概率分布的估计精度。显然，仅仅依靠决策人的经验做主观的估计，所设定的自然状态先验分布的精度不可能有很大的改进，因此需要通过随机试验去收集有关自然状态的信息，以便改进所设定的自然概率分布的准确性，从而改善决策分析的质量。贝叶斯分析可以通过随机试验获得观察值，去改进决策人设定的自然状态的先验概率，得到后验概率，从而减少期望损失。但是进行随机试验需要很高费用，为了解决先验概率准确性不足的缺点，同时避免得到后验概率需要投入大量人力、物力和财力的缺点，本文将马尔可夫链理论引入到决策过程中，从而保证即不用花费大量的投入，又能保证决策的准确性。

二、马尔可夫链理论

马尔可夫链最初由Markov于1906年研究而得名，它是一种特殊的参数离散、状态空间离散的随机过程，参数为T=｛0，1，2，…｝=N0，状态空间为可列S=｛1，2，…｝或有限S=｛1，2，…，n｝的情况。

设随机序列｛X（n）；n≥0｝的状态空间为S，如果对∀n∈N0，及i0，i1…，in，in+1∈S，P｛X（0）｝=i0，X（1）=i1，…，X（n）=in｝＞0，有：

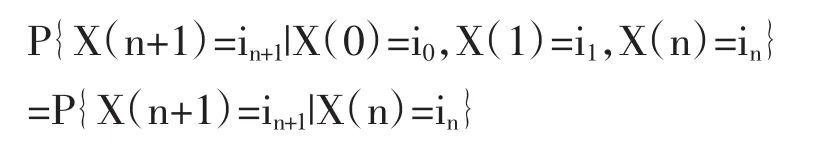
则称｛X（n）；n≥0｝为Markov链。

马尔可夫链具有Markov性或无后效性，简称为马氏性。设｛X（n）；n≥0｝为马氏链，状态空间为S，对于∀i，j∈S，称P｛X（n+1）=j｜X（n）=i｝=^pij（n）为马氏链｛X（n）；n≥0｝在n时刻的一步转移概率，其含义为n时刻系统处在i的条件下，下一时刻n+1系统处在j的可能性，又称为从状态i经一步转移到j的概率。若对∀i，j∈S，pij（n）≡pij，即pij与n无关，则称｛X（n）；n≥0｝为齐次Markov链。

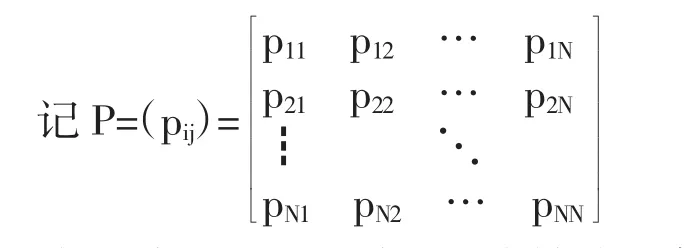
称P为｛X（n）；n≥0｝的一步转移概率矩阵，简称为转移矩阵。

一个定义在状态空间上的概率分布π＝｛π1，π2，…，πi，…｝称为马氏链的平稳分布，如有：π＝πP，即，平稳分布也称为马氏链的不变概率测度。对于一个平稳分布π，显然有：π=πP=πP2=…＝πPn。设｛Xn，n≥0｝是一马氏链，则｛Xn，n≥0｝为平稳过程的充分必要条件是π（0）＝（πi（0），i∈S）是平稳分布，即有：π（0）=π（0）P，这也给我们提供了求平稳分布的方法。通过对平稳分布的研究，我们可以得到系统长期运行中，处于各种状态的概率所具有的规律。

三、应用马尔可夫链理论解决风险型决策问题

如果决策问题存在n种自然状态为θ1，θ2，θ3…θn，可采取m种行动方案a1，a2，a3…am，并且知道每种行动方案在各种自然状态下的损失值，纪录过去各种自然状态出现的情况，用wij表示从状态i转移到状态j的个数，wi为处在状态i的个数，那么通过以计算出一步转移概率，则一步转移概率矩阵为：

通过前面的理论可得n步转移概率矩阵，P(n)=Pn，这样我们找到原来所处的状态，就可以知道系统n步转移后处在各种状态的概率，然后可以计算出采取各种行动方案损失的期望值，其中期望值最小的行动方案就是我们要采取的。

如果系统长期运行，可以通过前面的马尔可夫链平稳分布理论，求解方程π＝πP得到系统长期运行处在各种状态的概率。然后可以计算出采取各种行动方案损失的期望值，其中期望值最小的行动方案就是我们要采取的。

四、数值示例

设某决策问题存在θ1，θ2，θ3三种自然状态，可采取的行动方案包括a1，a2，a3三种。对过去20个星期的数据进行统计，得到表1，表2：

表1 前10周所处状态统计结果

表2 后10周所处状态统计结果

三种可供选择的方案其损失矩阵如表3：

表3 各方案损失矩阵

第21周及22周决策人应采取那种行动方案使损失最小，若从系统长期运行的角度考虑，决策人采取那种方案损失最小。

通过对表1，表2的数据进行统计可以得到处在状态θ1，θ2，θ3的概率为π（θ1）＝0.2，π（θ2）＝0.5，π（θ3）＝0.3（先验概率），该问题恰好与参考文献[1]中例4.1的问题一样，如果按照文献[1]中的最大可能值决策准则进行决策，决策人应该选择行动a1。如果按照文献[1]中的贝叶斯准则应选择行动a2，以上两种准则都是把将来发生的状态简单地用先验概率代替，这是不准确的。下面应用本文提供的方法进行决策。

用wij表示从状态i转移到状态j的个数，wi为处在状态i的个数，第20周无后续状态，不进行统计，统计结果为：

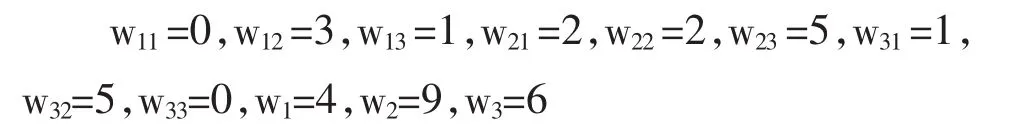
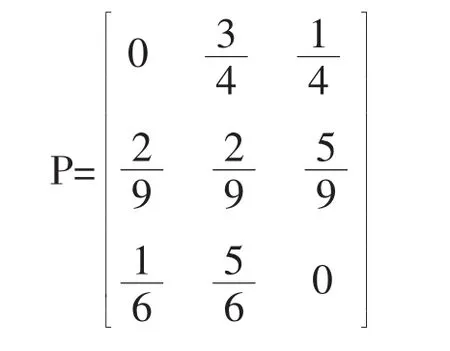
因为第20周处在状态θ2，由状态转移概率矩阵可知，21周处在状态θ1，θ2，θ3的概率分别为那么采取方案a1，a2，a3损失的期望值分别为E对应与行动方案a3的期望损失最小，所以决策人应选择行动方案a3。这与文献[1]中应用最大可能值准则，贝叶斯准则得到的结论都不相同。因为文献[1]中提供的决策准则都是把将来发生的状态简单地用先验概率代替，而本文提供的方法，通过预测将来各种状态发生的概率，并以此作为决策的依据，有助于减少决策失误，同时与文献[1]中提供的贝叶斯分析等方法相比，又减少了获取完全信息所需的费用。

应用数学软件maple，计算得两步转移概率矩阵为：

因为第20周处在状态θ2，由两步状态转移概率矩阵可知，21周处在状态θ1，θ2，θ3的概率分别为那么采取方案a1，a2，a3损失的期望值分别为E对应于行动方案a1的期望损失最小，所以决策人应选择行动方案a1。

系统长期运行下去，处于各个状态的概率趋于稳定，设处在a1，a2，a3的概率分别为π1，π2，π3，由前面的理论可知，π1，π2，π3应满足如下方程：

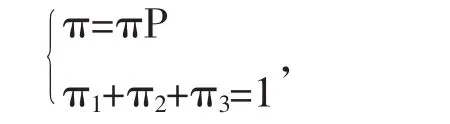
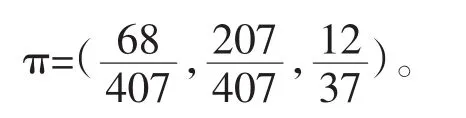
所以从系统长期运行的角度考虑，采取方案a1，a2，a3损失的期望值分别为

其中，π=（π1，π2，π3），应用数学软件maple，解得对应于行动方案a2的期望损失最小，所以决策人应选择行动方案a2。应用文献[1]中提供的方法无法对系统长期运行应该采取的行动方案进行决策，这是本文提出的决策方法的一个优点。

[1]岳超源.决策理论与方法[M].北京：科学出版社，2003.

[2]卫堂民.决策理论与技术[M].西安：西安交通大学出版社，2000.

[3]Sheldon M.Ross，Stochastic Processes[M]，John Wiley&Sons，1983.

[4]张波.应用随机过程[M].北京：中国人民大学出版社，2002.

[5]Edward P.C.Kao.An Introduction to Stochastic Processes[M].北京：机械工业出版社，2003.