浅谈信息系统灾难恢复能力的评估
荣楷
(赤峰市招生考试办公室,内蒙古 赤峰 024000)
浅谈信息系统灾难恢复能力的评估
荣楷
(赤峰市招生考试办公室,内蒙古 赤峰 024000)
随着社会信息化程度的加深,信息系统越来越广泛地应用在社会的各个领域中.使得信息安全防护成为社会发展中越来越关键的一部分.信息系统本身的复杂性决定了系统中不安全的因素总是存在.近几年国内国际接连不断地出现程度不同的灾难事件,对信息系统的容灾能力提出了巨大的挑战.由于灾难的不可预知性,我们无法完全避免灾难的发生.因此,建立完整、有效和规范的灾难恢复评估模型和方法,对信息系统灾难恢复能力进行评估,并据此建立更好的信息系统灾难恢复体系是保障信息安全的一项重要内容,是信息化发展建设的不可或缺的步骤.
灾难恢复;指标体系;层次分析法;因子分法;判断矩阵
近几年,国内国际接连不断地出现程度不同的灾难事件,对信息系统的容灾能力提出了巨大的挑战.因此,信息系统的灾难恢复能力的评估是十分必要的,我们不应该消极地等待灾难的到来,而是应该未雨绸缪地定期地对信息系统的灾难恢复能力进行评估,从根本上提升系统容灾能力.建立完整、有效和规范的灾难恢复评估模型、方法和相应的评估工具,对信息系统进行恢复性能评估,并据此建立更好的信息系统灾难恢复体系是保障国家信息安全的一项重要内容,是信息化发展建设的不可或缺的步骤.
1 常见信息系统灾难恢复能力评价方法
信息系统的灾难恢复工作起步很早,但是,针对信息系统的灾难恢复能力评估的研究却是刚刚开始.目前逐渐得到重视和应用的灾难恢复能力评价方法包括层次分析法,模糊综合评价法,因子分析法,BP神经网络法等.下面主要分析由于其自身的特色开始逐渐受到重视的因子分析法和BP神经网络法.
1.1 因子分析法
因子分析法是一种实用的多元统计方法,通过研究众多变量中的内部依赖关系来探求观察数据中的基本结构,并利用少数几个假想变量(因子)来反映原来众多所代表的信息.在进行盈利能力分析时,它的基本理念是将反映灾难恢复能力指标中的公共因素提取出来,再利用这些公共因子对信息系统的灾难恢复能力再进行综合评价.
设一共有k个反映信息系统灾难恢复能力的指标,记为X 1,X 2,X 3,…X k.则这些受到某种共同因素影响的灾难恢复能力指标会发生相互重叠,于是可以利用假想变量f 1, f 2,……f m(m 其中i=1,2,…k.u i称为特殊因子,表示该变量不能被公共因子所解释的部分.记hi2为共同度,具体计算公式为: 因子载荷aip的值通常可以结合主成分分析法进行具体计算来求得.那么,当其越接近于1,说明原观察变量能被公因子说明的程度越高. 然后,进行样本综合评价,计算因子对应每个样本上的值,即因子值.其中第p个因子在第i个样本上的值上的计算公式为: 因子和第j个变量之间的因子值系数xji是第j个变量在第i个样本上的值. 最后,我们可以通过求取因子f i的加权平均值来反映企业的盈利能力.具体计算公式是: 其中k p是第p个公因子的方差贡献率. 通过因子分析法可以观察到影响灾难恢复能力的原始指标的内在基本结构,揭示对灾难恢复能力具有重大影响的指标及其相关的因素.这是因子分析法的优势所在.同时,因子分析法的权重来源于统计所取得的样本,较少受到人为因素的影响,较为客观.不过其给出的评价结果一般对决策或者排序比较有效,因为其有时并不能反映现实评价中评价目标的真实重要性程度,而且在应用时要求评价对象的各因素必须具有充分的样本.而且因子分析法一般只能处理若干个单层次的指标,缺乏处理复杂系统问题的能力,并且没有处理定性因素的能力,因而在使用上受到了一定限制. 1.2 BP神经网络法 由于信息系统灾难恢复能力测评是对构成它的一系列指标进行定性和定量相结合的研究而进行的综合测评,由于指标数目繁多,内容复杂而且信息本身具有模糊性,所以可以采用具有学习能力和容错能力的神经网络法进行处理. 典型的BP网络结构包括输入层、隐含层和输出层,每层都有若干个相互独立的神经元节点,但相邻两层之间的神经元节点通过相互之间的权重进行连接和并按照一定的数学模式进行信息交互. 运用BP神经网络法进行灾难恢复能力评估,首先要合理科学地选取若干具有代表性的灾难恢复能力指标作为网络的输入矢量X=(x 0,x 1,x 2,x 3,…,x n)T,然后可将代表相应综合测评结果的分值作为神经网络的期望输出值.当用足够的灾难恢复能力的样本训练这个网络,经过不断学习使相对误差符合预定精度时,当神经网络所含有的相应权值和闭值就是网络经过自适应学习所得到的正确内部表示.即通过反复训练,调整网络的权重和阂值,使得仿真结果和期望输出值的相对误差控制在2%以下,此时,即可用来对不同评价对象的灾难能力进行合理的盈利能力评价.其中,神经网络的输出值一般经由专家评价法对样本信息系统的灾难恢复能力进行评价来取得. 由于信息系统灾难恢复能力指标之间存在相互影响且呈现出复杂的非线性关系和模糊性,人工神经网络与传统的方法相比,原理简单,拟合的精度高,可以避免工作过程中可能出现的大量计算及人为主观上的失误,在一定程度上解决了信息的模糊性.对于企业自身来说,不需要花费大量的人力、物力、财力去收集数据资料等来建立该网络模型,可操作性强,并且训练好后网络有着较好的通用性.不过,在建立模型的过程中,该方法不可避免地需要设定期望输出值,而带有浓厚的主观色彩.而且,它无法有效处理定性指标和多层次的指标. 基于层次分析法的模糊综合判断,是指运用模糊数学理论与层次分析法相结合,在利用层次分析法确定指标体系权重的基础上,进一步结合模糊数学分析方法进行综合评价,对社会经济以及科学管理领域中的复杂问题进行研究和评价的一种方法. 该方法首先利用层次分析法分析复杂的社会经济以及科学管理领域中的问题,确定指标体系中的各个指标的相对权重.层次分析法(Analytic Hierarcy Proc ESS)由美国匹兹堡大学教授、著名运筹学家T.L.saaty于20世纪70年代中期提出,简称AHP法,是一种系统分析的方法.它将一个复杂的多指标评价问题作为一个系统,按照因素间的相互关系影响,首先将总目标分解为多个分目标或准则,再分解为多指标的若干层次,最后通过定性指标模糊量化方法算出总排序和层次单排序,以此确定多目标优化决策问题中各个指标的权重.然后,以模糊数学理论为基础,应用模糊关系合成的原理,将一些边界不清,不易定量的因素定量化,对规律不确定性事物的进行整体评价. 在上述建立的信息系统灾难恢复能力指标体系中,每个层次以及每个评价层次下面的评价因素和指标的重要程度是有所差异的,应该用不同的权重来描述这种差异性.确定权重的方法很多,常用的有层次分析法、专家评价法、德尔菲法和因子分析法等.科学合理,而且层次分明,易于掌握的层次分析法是其中很重要的一种方法. 在多目标、多层次决策时候,所分析、比较、评价的各个因素往往含有模糊性,其中的优先度和重要性难以准确科学地量化比较,所以我们不仅要重视定量因素的作用,而且要发挥决策者的主观选择,把定性和定量研究有效地结合起来.由于本文影响信息系统灾难恢复能力的因素往往含有模糊性,因此可以选用层次分析法确定信息系统灾难恢复能力评价指标体系中各个指标的权重. 3.1 建立指标体系层次结构 第一步,建立合理的多层次指标体系.首先,要明确我们的研究对象和属性,科学地根据指标设计原则建立起指标体系,对该指标体系中的指标进行分类,按照不同的属性分为不同的小类.也就是说,将上述指标分为若干大类和小类,同一等级的类别形成了一个互不交叉和保持独立的层次,从而形成不同的层次.同一层次的元素作为准则层,对下一层次的全部元素起到支配的作用,最后形成自上以下的逐层支配关系的“目标层——准则层——具体指标层”的多层次结构.如图1所示. 图1 多层次指标体系结构图 3.2 建立判断矩阵 “1-9”标度法判断矩阵及其意义 第二步,建立比较判断矩阵.根据上述的多层次指标体系,假定上层的元素U作为目标,对下层的元素U 1,U 2,U 3…具有支配关系.在元素U 1和U 2,U 1和U 3,……之间作两两比较,判断哪一个元素更重要,并且用l、3、5、7、9表示出来.1、3、5、7、9作为相对重要性的比例标度,具体含义如下表2所示.例如,如果U l和U 2同等重要,那么则用1作为判断数来表示它们的相对重要程度.反之,U 2比U 1的判断数为U 1对U 2的判断数的倒数.判断数U i j表示对U而言,U i比U j的相对重要性程度.显然有,U i i=1,U i j=l/U j i,U i j>0. 根据上述的评价标准,就可以邀请有责任感且内行的多位专家参与估计判断数.一般来说,判断矩阵的估计关系到决策质量,因此人员结构与专家数目应该特别慎重. 通过访谈和向专家发放相关的调查问卷,我们就可以获得相关评价数据来建立判断矩阵,进行相关指标重要程度的两两比较了.调查问卷应该包括各个指标的内涵,评价标准,评估表格和其它相关内容. 3.3 层次单排序 第三步,进行层次单排序.在准则U下,对n个元素U l,U 2…U n排序权重计算,可以求解判断矩阵P的最大特征根λmax,该特征根满足公式: 其中W为对应最大特征根λmax的特征向量,其分量为w i(i=1,2…n)为对应元素U 1,U 2…U n在准则U下单排序下的权重,称为该层次的单排序. 第四步,计算相对权重.重复利用特征向量法计算同层次指标相对于上一层次指标的相对权重.特征向量W的常用计算方法很多,包括计算机软件,“方根法”和“和积法”等. 第五步,进行一致性检验.由于各位专家自身经历和知识结构的不同,给出的判断结果也可能会有所不同,所以上面计算获得的判断矩阵未必具有一致性,而只有当判断矩阵具有完全一致性或者满意一致性时,层次分析法才具有显著效果,所以要对前面获得的判断矩阵进行一致性检验. 根据数学的一般原理,对于N阶判断矩阵来说,最大特征根为单根,并有λmax>=n.简单来说,当λmax=n,其余特征根均为0时,则U具有完全一致性.如果λmax稍大于n,而其余特征根接近于0时,则U具有满意的一致性.具体来说,可以通过计算一致性指标来检验判断矩阵的一致性: 当C I=0的时候,判断矩阵具有完全一致性,反之,完全一致性不具备.R I为判断矩阵的平均随机一致性指标,具体如下表3-3所示.C R为判断矩阵的随机一致性比例,等于判断矩阵的一致性指标C I与同阶平均随机一致性指标R I值之比.即: 当C R=0,即C I=0时,判断矩阵具有完全的随机一致性.可见,当判断矩阵具有完全一致性时,即具有完全的随机一致性.而当C R<0.10时,则判断矩阵具有满意的一致性,其对应的特征向量各分量即是各个指标的权重.当C R>0.10时,判断矩阵P应再进行调整,使之具有满意的一致性. 第六步,确定各个指标的相对权重.当CR1,CR2… CRn<0.10时,那么各判断矩阵具有满意的一致性,则各判断矩阵的特征向量可视为相应指标的权重. 平均随机一致性指标 由于该评估方法是建立在新的规范基础上的,根据掌握的资料,目前国内在这方面的研究还处于初级阶段,所以这一评估方法的提出可以为国家将来在信息系统灾难恢复能力评估方面的标准细则提供参考. 〔1〕姜启源.数学模型.北京:高等教育出版社.1993. 〔2〕DRI International.Professional Practices for Business Continuity Planners.http://www.chinacissp.com/download/ProfessionalPractices.pdf,2002. 〔3〕卢泰宏.信息分析.广州:中山大学出版社,1998:185-222. 〔4〕赵焕臣,许树柏,和金生.层次分析法.北京:科学出版社,1986. 〔5〕张跃,邹寿平,宿芬.模糊数学方法及其应用.北京:煤炭工业出版社,1992. TP393 A 1673-260X(2010)07-0038-03


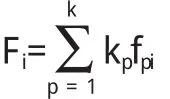
2 基于层次分析法的模糊综合评价体系的基本原理
3 基于层次分析法确定指标权重


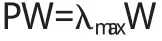



4 总结

