剩余格的准滤子拓扑空间

刘春辉，秦学成

（赤峰学院 初等教育学院，内蒙古 赤峰 024000）

剩余格的准滤子拓扑空间

刘春辉，秦学成

（赤峰学院 初等教育学院，内蒙古 赤峰 024000）

在剩余格上引入了准滤子和剩余格间的蕴涵同态的概念，给出了准滤子的若干性质;讨论了准滤子与滤子间的关系;指出了剩余格上全体准滤子构成一个拓扑；证明了剩余格之间的同构映射是相应拓扑空间之间的一个同胚.

剩余格；(准)滤子；蕴涵同态；拓扑空间；同胚

1 引言和预备

非经典数理逻辑的一个重要研究方向是对有关逻辑代数系统的研究.随着数学和计算机科学的迅速发展,非经典数理逻辑已成为人工智能领域的最具活力的研究方向之一.而非经典数理逻辑的一个重要方向是对逻辑代数系统的研究,这方面的研究成果不仅促进了非经典数理逻辑的发展,也丰富了代数学的内容[1-2].在众多的逻辑代数系统中,由Pavelka教授引入的剩余格是比较重要且应用相当广泛的代数系统.Pavelka以Lukasiewicz公理系统为背景,将剩余理论引入到模糊逻辑的研究中,建立了一类相当宽泛的逻辑结构,并在此基础上成功的解决了Lukasiewicz公理系统的完备性问题[3].在现代模糊逻辑的理论中,剩余格是公认的最重要的代数结构,它已成为模糊逻辑中相当理想的代数框架.更值得注意的是,非经典数理逻辑中基于不同的蕴涵算子而构造出来的许多逻辑代数系统,诸如MV-代数[4],R0-代数[4]和格蕴涵代数[5]等都是基于剩余格而提出的.所以对剩余格的性态作深入的研究,将有助于把握各种逻辑代数的共同特征.

在逻辑推理系统和逻辑代数系统的研究中,滤子是一个重要的概念.各种逻辑代数系统中滤子的性质及它们的应用已得到了广泛的研究[6-10].本文笔者在剩余格上引入了准滤子和剩余格间的蕴涵同态的概念.讨论了准滤子的若干性质及其与滤子间的关系;指出了剩余格上全体准滤子构成一个拓扑,证明了剩余格之间的同构映射是相应拓扑空间之间的一个同胚.为利用拓扑学的工具研究非经典数理逻辑问题奠定了重要的基础.

为了讨论的方便,首先给出一些预备知识,有关偏序的知识见[11],有关拓扑的内容见[12].

定义1.1[1]设P是一个偏序集,称P上的二元运算⊗和→是互为伴随的,如果以下条件成立:

(1)⊗：P×P是单调递增的;

(2)→：P×P→P关于第一变量是不增的,关于第二变量是不减的;

(3)a⊗b≤c当且仅当a≤b→,∀a,b,c∈P.

此时称(⊗→)为P上的伴随对.

定义1.2[3]三元组 (L,⊗,→)称为剩余格(Residuared Lattice),如果

(1)L是有界格,最大元是1,最小元是0;

(2)(⊗,→)是L上的伴随对;

(3)(L,⊗,→)是以1为单位元的交换半群.

定义1.3[3]设(L,⊗,→)是剩余格,Ø≠⊕⊆L.称F为L的一个滤子,如果∀a,b∈L有:

(1)1∈F;

(2)如果a∈F且a≤b,则b∈F;

(3)如果a,b∈F,则a⊗b.

本文我们将剩余格上的滤子全体之集记为F(L).

引理1.4[3]设(L,⊗,→)是剩余格且Ø≠F⊆L.则F∈F (L)当且仅当下列两个条件成立:

(1)1∈F;

(2)如果a,a→b∈,则b∈F.

定义1.5[12]设X和Y是两个拓扑空间,f:X→Y为一个映射.如果Y中每一开集U的原像f-1(U)都是X中的开集,则称f是从X到Y的一个连续映射.

定义1.6[12]设X和Y是两个拓扑空间,f：X→Y一个双射.如果f和f-1：Y→X都是连续映射,则称f是一个同胚映射或同胚.

2 准滤子的定义与性质

本节我们在剩余格中引入准滤子的概念,并给出它的一些基本性质.

定义2.1设(L,⊗,→)是一个剩余格,Ø≠⊕⊆L.∀a,b∈L,如果当a→b∈F时都有a→(a→b)∈F,则称F是L的一个准滤子.L的准滤子全体之集记为PF(L).

注2.2容易验证剩余格(L,⊗,→)的任意一族准滤子的交和并都还是L的准滤子.即PF(L)对集合的交与并都是封闭的.

定理2.4设(L,⊗,→)是剩余格,a→b∈F.如果F∈F(L),则F∈PF(L).

证明 ∀a,b∈L,设a→b∈F.由于 (a→b)→(a→(a→b)) =1∈F∈F(L),故由引理1.4(2)和F∈F(L)便得a→(a→b)∈F.即F∈PF(L).

上述定理指出了剩余格中的每一个滤子都是准滤子.下面我们用一个具体的实例说明该定理的逆命题是不成立的,从而表明引入定义2.1的合理性.

例2.5设L={0,a,b,c,d,1},其上偏序关系由图1给出,在L上规定→和⊗如表1和2所示.则可以验证（L，⊗，→）是一个剩余格.取F={0，a，1},则F∈PF（L）.但F∉F（L）,因为0∈F且0→c=1∈F,然而c∉F.

设（L，⊗，→）是一个剩余格,我们引入如下记号:

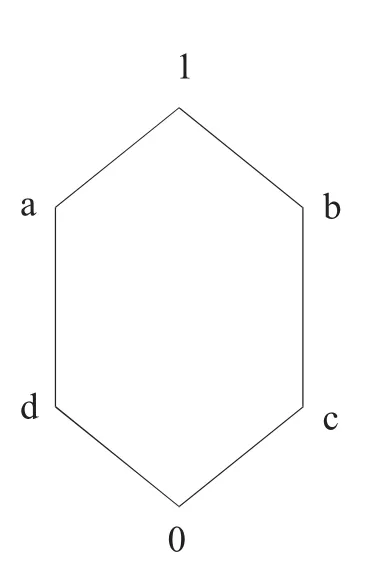
图1

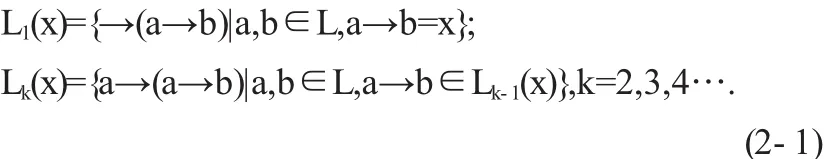
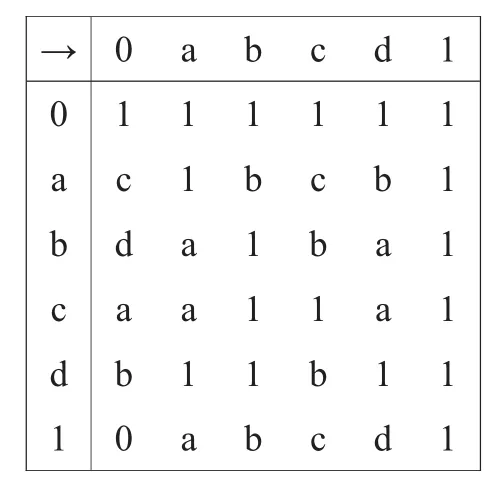
表1

表2

定理2.6设（L,⊗,→）是剩余格,则∀x∈L,F(x)∈PF(L).

证明 ∀a,b∈L,如果a→b∈F(x),则∃k∈□*使得a→b∈Lk(x).于是由(2-1)式可知a→(a→b)∈Lk-1(x)⊆F(x),故由定义2.1便得F(x)∈F(x).

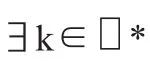
(1)a1→b1=x;

(2)ai→bi∈Li-1(x)且ai→bi=ai-1→(ai-1→bi-1),i=2,3,4,…,k;

(3)a=ak→(ak→bk).

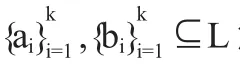
定理2.8设（L,⊗,→）是剩余格,则∀x∈L,F(x)=〈x〉.

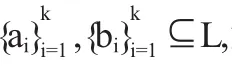
(1)a1→b1=x;

(2)ai→bi∈Li-1(x)且ai→bi=ai-1→(ai-1→bi-1),i=2,3,4,…,k;

(3)a=ak→(ak→bk).

故ai→bi∈〈x〉,i=1,2,…,k.从而由〈x〉∈PF(L)便得a=ak→(ak→bk)∈〈x〉.于是又得F(x)⊆〈x〉,进而F(x)=〈x〉.

3 剩余格上的准滤子空间

设(L,⊗,→)是剩余格,由注2.2知PF(L)对集合的交与并都是封闭的,且显然L∈PF(L).现在我们令TL=PF(L)∪{Ø},则易知（L，TL）构成一个拓扑空间,称之为L上的准滤子空间.为了研究此空间的性质,首先引入如下定义.

定义3.1设(L,⊗,→)和(M,⊗*,→*)是两个剩余格,称映射f：L→M是从L到M的蕴涵同态,如果∀a,b∈L都有f(a→b)=f(a)→*f(b).若f是还一个双射,则称f是从L到M的蕴涵同构.

定理3.2设(L,⊗,→)和(M,⊗*,→*)是两个剩余格,f：L→M是从L到M的蕴涵同态,则∀x∈L，∀n∈□*,f(Ln(x))⊆Mn(f(x)).

证明 对自然数n做数学归纳法.当n=1时,∀n∈L1(x),由L1(x)的定义知∃a,b∈L使得u=a→(a→b)且a→b=x.而f是从L到M的蕴涵同态,故f(u)f(a→(a→b))=f(a)→*(f(a)→*f(b))且f(a)→*f(b)=f(a→b)=f(x),故f(u)∈M1(f(x)).从而f(L1(x))⊆M1(f(x)),即结论对n=1成立.

假设当n=k时结论成立,即f(Lk(x))⊆Mk(f(x)).则当n=k+1时,∀n∈Lk+1(x),则∃a,b∈L使得u=a→(a→b)且a→b∈Lk(x),故由归纳假设可以得f(a)→*f(b)=f(a→b)∈f(Lk(x))⊆Mk(f(x)),故f(u)=f(a)→*(f(a)→*f(b))∈Mk+1(f(x)),这说明结论对n=k+1也成立.有归纳法原理便得∀x∈L，∀n∈□*,f(Ln(x))⊆Mn(f(x)).

定理3.3设(L,⊗,→)和(M,⊗*,→*)是两个剩余格,f：L→M是从L到M的蕴涵同构,则∀x∈L，∀n∈□*,f(Ln(x))⊆Mn(f(x)).

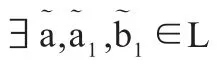
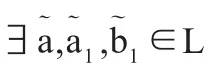
定理3.4设(L,⊗,→)和(M,⊗*,→*)是两个剩余格,f:L→M是从L到M的蕴涵同态,则∀x∈L,f(〈x〉)⊆〈f(x)〉.

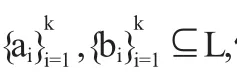
(1)a1→b1=x;

(2)ai→bi∈Li-1(x)且ai→bi=ai-1→(ai-1→bi-1),i=2,3,4,…,k;

(3)a=ak→(ak→bk).

于是由f是为蕴涵同态可得

(1*)f(a1)→*f(b1)=f(x);

(2*)f(ai)→*f(bi)∈Mi(f(x))且f(ai)→*f(bi)=f(ai-1)→8(f(ai-1)→*f (bi-1)),i=2,3,4,…,k;

(3*)f(a)=f(ak)→*(f(ak)→*f(bk)).

故再由引理2.7和定理2.8便得f(a)∈f(〈x〉),从而f(〈x〉)⊆〈f(x)〉.

定理3.5设(L,⊗,→)和(M,⊗*,→*)是两个剩余格,f:L→M是从L到M的蕴涵同构,则∀x∈L,f(〈x〉)=〈f(x)〉.

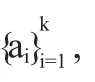
(1)a1→*b1=f(x);

(2)ai→*bi∈Mi-1(f(x))且ai→*bi=ai-1→*(ai-1→*bi-1),i=2,3,4,…,k;

(3)a=ak→*(ak→*bk).

于是由蕴涵同构f为单射便得

所以u∈〈x〉,从而a=f(u),即〈f(x〉⊆f(〈x〉).进而f(〈x〉)⊆〈f(x)〉.

由定理3.5立即可得如下推论:

推论3.6设(L,⊗,→)和(M,⊗*,→*)是两个剩余格,f:L→ M是从L到M的蕴涵同构,则∀U∈TL都有f(U)∈TM.

定理3.7设(L,⊗,→)和(M,⊗*,→*)是两个剩余格,f:L→M是从L到M的蕴涵同构,则f为从拓扑空间(L,TL)到(M,TM)的一个同胚.

证明 任取U∈TM,记f-1(U)={a∈L|f(a)∈U}.∀a,b∈L,如果a→b∈f-1(U),则f(a)→*f(b)=f(a→b)∈U,而U∈PF(M),故结合f为蕴涵同构便得

f(a→(a→b))=f(a)→*(f(a)→*f(b))∈U.于是a→(a→b)∈f-1(U),从而便得f-1(U)∈TL.故f是从拓扑空间(L,TL)到(M,TM)的一个连续映射.类似可证f-1:M→L也是连续映射.又f是双射,故由定义1.6可知f为从拓扑空间(L,TL)到(M,TM)的一个同胚.

限于篇幅,关于准滤子拓扑空间(L,TL)的拓扑性质我们将另文讨论.

〔1〕王国俊.非经典数理逻辑与近似推理[M].北京:科学出版社,2006.

〔2〕王国俊.数理逻辑引论与归结原理(第二版)[M].北京:科学出版社,2006.

〔3〕Pavelka.J.On fuzzy logic(I;II;III)[J].Z.Math.Logic Grund.Math.1979,25:45-52;119-134;447-464.

〔4〕王国俊.MV-代数,BL-代数,R0-代数与多值逻辑[J].模糊系统与数学，2002,16(2):1-15.

〔5〕徐扬.格蕴涵代数[J].西南交通大学学报,1993,28(1):20-27.

〔6〕Liu LZ,Li KT.Fuzzy filters of BL-algebras[J].Information Science.2005(173):141-154.

〔7〕Liu Y L,Liu SY,Xu Y,Qin K Y.ILI-ideals and prime LI-ideals in lattice implication algebras[J].Information Sciences.155(2003):157-175.

〔8〕张家录.R0-代数的MP滤子格 [J].模糊系统与数学，2006,20(3):26-33.

〔9〕Jun Y B,Roh E H,Xu Y.LI-ideals in lattice implication algebras[J].Bull.Korean Math.Sc.1998,35(1): 13-23.

〔10〕张小红,薛占熬,马盈仓.NM代数的布尔NP滤子与布尔MP理想[J].工程数学学报，2005，22(2):287-294.

〔11〕GIERZ G,HOFMANN K H,KEIMEL K,etc.Continuous lattices and domain [M].London:Cambridge University Press,2003.

〔12〕熊金城.点集拓扑学讲义(第三版)[M].北京:高等教育出版社,2003.

O141.1；O153.1

A

1673-260X（2010）02-0004-03