以太的兴衰

孙元和

（赤峰学院 物理与电子信息工程系，内蒙古 赤峰 024000）

以太的兴衰

孙元和

（赤峰学院 物理与电子信息工程系，内蒙古 赤峰 024000）

以太是牛顿绝对时空观的理论基础，曾在经典物理学的发展中起到了不可忽视的作用.探索以太的存在及其性质，对人类的时空观、物质观、运动观和宇宙观都具有重大的历史意义.

以太；以太漂移；绝对时空

1 以太学说的起源

在物理学思想的发展中，“以太”是作为一种特殊物质被引进物理学的.笛卡尔1644年发表的《哲学原理》中也引用了以太的观念.他认为由于太阳周围以太出现漩涡，才造成行星围绕太阳的运动，为了解释物体之间的作用力，特别是万有引力现象，最先赋予了以太某种力学性质.在他看来，空间被以太这种连续的媒质所充满，物体之间的所有作用力都是通过以太的应变和运动来传递的，不存在任何超距作用.1678年惠更斯把光振动类比于声振动，看成是以太中的弹性脉冲，以太又充当了光波的载体.因为按照当时的力学理论，任何波动都是某种媒介物质的力学振动的传播.由于光可以在真空中传播，因此以太必然是充满全部空间的，包括真空和对于光是透明的各种物体之中.但是后来由于光的微粒说占了上风，以太理论受到压抑.

1800年以后，由于波动说成功地解释了干涉、衍射和偏振等现象，以太学说重新抬头.在波动说的支持者看来光既然是一种波，就一定要有载体存在.光能通过万籁俱静的虚空，证明虚空中存在充满这种载体，这种载体就是以太.随着光的波动说的复兴，作为传播光波的媒介，以太又成为物理学所不可或缺的一种“客观实在”.法拉第把以太看作是力线的荷载体；而麦克斯韦则设想用以太的力学运动对电磁现象作出解释.他所提出的光的电磁理论，又把产生电磁现象的媒介和光以太统一起来.在电磁波以光速传播的预言被证实后，以太的存在便在物理学界获得了广泛的承认.

2 以太的特殊性质

为了解释光和电磁现象，必须赋予以太一些奇妙的性质.在19世纪，人们提出了各种各样的以太模型，但都无法摆脱以太的神秘色彩.仅仅从参照系的观点看来，如果光是在以太中的传播过程，相对于静止的以太，光或电磁波的传播速度必是各向同性的.事实上，在麦克斯韦的电磁学方程组里就出现一个常数c，它表明电磁波在真空中总是以不变的速度c向各个方向传播，是各向同性的.但是按照经典的速度合成法则，相对于以太静止和相对于运动的两种参照系，或者更广义地说在不同的惯性系中，光或电磁波沿不同方向的速度就会出现明显差别，不会是都等于c的.若如此，就应该存在一个特殊的参照系，在这个参照系里，麦克斯韦方程组才取标准形式，而对于其它参考系，麦克斯韦方程组都不应成立.这就是说，对于电磁现象的研究，可以定义一个最优惯性系，即相对于以太静止的参照系，这实际上就是牛顿的“绝对空间”，而且利用在静止以太中以太恒定速度传播的光信号，又可以确定出在宇宙中一切地点都同步的“绝对时间”.这样，充满整个宇宙的绝对静止的以太，就成了牛顿绝对时空的物质框架.因而通过“以太漂移”的实验探索以太的存在状态，就成了非常重要的问题.

3 以太的消亡

由于以太是一种假想的“物质”，为了解释光和电磁现象，只能根据光和电磁现象的行为推测以太的特性，却无法直接用实验证明以太的存在.人们从不同的角度提出有关以太的模型，得到的是相互矛盾的结论.例如有人认为以太是一种无处不在、绝对静止、极其稀薄的刚性“物质”.1804年托马斯.杨写道“光以太充满所有物资之中，很少受到或不受阻力，就像风从一小丛林中穿过一样.”也就是说，地球在以太的“汪洋大海”中遨游，在地球和以太之间，必有相对运动.那么运动物体是否对以太有影响，也就是说以太是否会被运动物体所拖曳，是全部拖曳、部分拖曳还是根本不拖曳？在“以太漂移”的观测和研究中，产生了许多令人困惑的难题.

3.1 光行差的观测

1728年英国天文学家布拉德雷（J.Bradley, 1693～1762）所发现的“光行差”现象，可以看做是关于“以太漂移”的早期观测.他发现从地球上观测一颗遥远的恒星，利用光行差公式可以算出c=3.04× 105千米/秒，这是最早的光速值.这个计算结果与实际观测完全符合.光行差现象意味着，太阳相对于以太是静止的，地球则以绕日公转速度v在以太海洋中穿行，丝毫不对以太有拖拽作用.

3.2 阿拉果的望远镜实验

如果以太完全不被地球拖曳，运动着的地球就应感到有“以太风”，这种以太风将会对从不同方向射到地球的星光产生不同的影响，1810年法国科学家阿拉果用望远镜观察来自不同方向恒星光线，企图发现由“以太风”的作用而产生的这种效应，却意外地得到了否定的结果.

3.3 菲涅耳提出部分曳引假说

1818年，菲涅耳在得知阿拉果的结果后，为了使两个实验的结果能够协调，提出了部分曳引假说.他指出，只要假设以太有确定的一部分被运动物质曳引，就可以同时使布莱德雷和阿拉果的实验得到解释.他假设，整个宇宙间的以太是静止着的，在以太中运动着的透明物体，本身并不拖曳着与真空中密度相同的这部分以太一起运动.但是，透明物质按其折射率n的大小，吸收了比真空中更稠密的以太，超过真空密度的这部分以太，将被透明物质拖曳着一起运动.菲涅耳假设，介质内的以太密度同它的折射率n的平方成正比，因此，介质内超出真空的那部分以太的密度应该同n2－1成比例，这超出部分占介质内以太总数的份额便是：

这就是菲涅耳的“曳引系数”.因此，对于以速度v运动的、折射率为n的介质中的光速c'有菲涅耳公式：

c/n为静止介质中的光速，后一项即“曳引”项，在真空中，由于n=1，曳引系数为零，就回到了布莱德雷的条件.1871年，英国天文学家艾里（G.B.Airy, 1801～1892）用充水的望远镜测量了光行差，证实了菲涅耳的预言.

与菲涅耳相反，英国物理学家斯托克斯（G.G. Stokes,1819～1903）却不相信物体可以在以太中自由穿行而不生扰动.他于1845年提出了以太被运动物体全部拖曳的假说.他认为，地球将把贴在它表面上的那层以太完全拖曳走，离地面愈高，这种拖曳就愈减弱，直至很远处以太完全不受影响而静止不动.他的结果能推导出菲涅耳的曳引系数，也可解释阿拉果的实验.但是由于不久就有斐索的流水实验支持了菲涅耳，所以斯托克斯的假说没有受到重视.

3.4 斐索的流水实验

菲索的流水实验

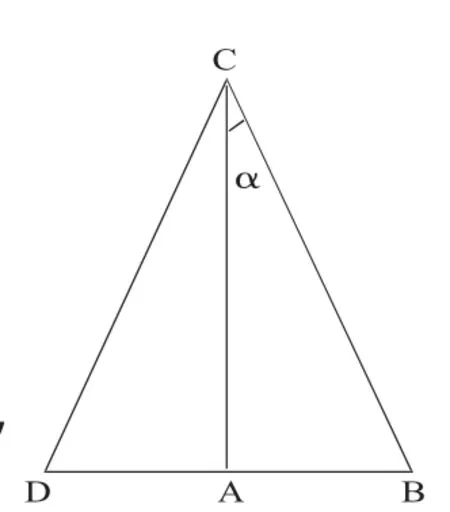
1851年，法国物理学家斐索（A.H.L.Fizeau, 1819～1896），用干涉方法测定流水中的光速，以检验光在运动的透明物体中的速度是否发生变化.在图中他让一束单色光经半镀膜玻璃片的反射与透射分为两束相干光，让它们沿相反方向被反射镜反射沿一闭合线再会聚到一起产生干涉条纹.在行进中一束光穿过同向流动的水，另一束光则逆向穿过这同一水流.斐索的实验以及后来的改进型的实验，都证实了菲涅耳的以太部分拖拽假说.

1868年霍克用更为严密的以太漂移实验，进一步证实了菲涅耳的部分曳引假说，从而使这一假说成了以太理论的重要支柱.但由它引出的另一条结论，那就是当n=1时，曳引系数等于零.以太应该处于静止.物体在以太中运动，从物体上看，就好象以太在漂移.地球沿轨道绕太阳运转，也必沿相反方向形成以太风.这就给人们提供一种可能的途径，通过测量以太相对于地球的漂移速度，来证实以太的存在和探求以太的性质.

3.5 迈克耳逊—莫雷实验

直到1879年还没有一个实验能测出以太漂移速度.麦克斯韦在为《大英百科全书》撰写的《以太》条目中写到：“如果可以在地面上从光由一站到另一站所经时间测到光速，那么我们就可以比较相反的方向所测速度，来确定以太相对于地球的速度.然而实际上地面测光速的各种方法都取决于两站之间的往返行程所增加的时间，以太的相对速度等于地球轨道速度，由此增加的时间仅占整个传播时间的亿分之一，所以的确难以观察.”这种实验所观测的相对时间变动可由下式计算：

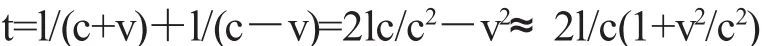
这是一个v/c的二阶效应.

麦克斯韦关于地面上双程光路实验不可能检测到(v/c)2这样微小的效应的这段话引起了迈克耳逊的注意，并与1881年春天利用他发明的迈克尔孙干涉仪进行了著名的以太漂移的第一次观测.但结果却出乎意料，迈克耳逊做出了静止以太的假设是不正确的结论.

迈克耳逊1881年的实验遭到怀疑，在1886年他和莫雷合作，进一步改进干涉仪实验.1887年7月，他们完成了测量工作，这就是历史上著名的以太漂移实验的“零结果”.从那以后许多人不断提高精确度运用这种类型实验，去探测地球相对于以太的速度，得到的都是否定的结果.

3.6 洛奇的转盘实验

迈克耳逊—莫雷实验的结果对菲涅耳部分曳引假说是一个致命打击.迈克耳逊和莫雷倾向于斯托克斯的完全曳引假说，但是从斯托克斯的完全曳引假说出发，必然会引出一个结论，即在运动物体表面有一速度梯度的区域.如果靠得很近，总可以察觉出这一效应.

洛奇钢盘实验原理图

于是英国物理学家洛奇在1892年做了一个钢盘转动实验，以试验以太的漂移.他把两块靠得很近的大钢锯圆盘平行的安装在电机的轴上，让它们高速旋转.一束光线经半镀银面分成相干的两路，分别沿相反方向，绕四方框架在钢盘之间走三圈，再会合于望远镜产生干涉条纹.

如果钢盘能带动其附近的以太旋转，则两路光线的时间差会造成干涉条纹的移动.但是，不论钢盘转速如何，钢盘正转与反转造成的条纹都是微不足道的.洛奇的钢盘实验结果导致人们对斯托克斯的完全曳引假说也失去了信心，这就迫使人们接受非兹杰拉德在1889年和洛伦兹在1892年分别提出的收缩假说.

爱因斯坦创立狭义相对论以后，利用光速不变原理对上述实验和原理都可以做出科学解释，而无需构造任何具体的以太模型，伴随以太的消亡，牛顿的绝对时空观被否定，物理学进入了一个新的时代.

〔1〕郭奕玲，沈慧君.物理学史（第2版）.清华大学出版社.

〔2〕李艳平，申先甲.物理学史教程.科学出版社.

〔3〕东南大学等七所工科院校.物理学（第五版）.高等教育出版社.

〔4〕程守洙，江之永.普通物理学（第五版）.高等教育出版社.

O4-1

A

1673-260X（2010）02-0011-03