下承式钢桁结合梁桥的畸变分析✳
陈玉骥,罗旗帜
(佛山科学技术学院 土木工程与建筑系 ,广东 佛山 528000)
0 引 言
钢桁结合梁桥属于板桁组合结构体系,目前对这种体系的研究还不多[1-5],且主要针对的是上承式结构.高速铁路钢桁结合梁桥以下承式居多,其受力特性与上承式有所不同.高速铁路下承式钢桁结合梁桥一般为双线桥,其活载有双线活载和单线活载(即偏载).在偏载作用下,下承式钢桁结合梁桥除了弯曲、轴向变形外,还将产生扭转和畸变变形.可见,结构的变形十分复杂.为了确定下承式钢桁结合梁桥在偏载作用下的解,可先将荷载进行分解,即将偏载分解为双线对称荷载与双线反对称荷载的迭加.后者(即结构上纵梁处的反对称荷载,见图1(a))(图1为下承式钢桁结合梁横截面示意图,其中:上翼缘为上平联,下上翼缘为钢-砼组合桥面系,腹板即为腹杆)还可再分解为主桁下弦杆处的反对称荷载(图1(b))和自平衡荷载(图1(c))的迭加(图中,p 1=pa/B).自平衡荷载只会使桥面板产生应力与变形,可按薄板弯曲理论进行分析;而反对称荷载(图2(a))又可分解为刚性周边不变形的纯扭转荷载(图2(b))与畸变荷载(图2(c))的迭加(图中,p 2=pa/2B,p 3=pa/2H).文献 [6-7]已对下承式钢桁结合梁桥在双线荷载和纯扭转荷载作用下的受力状态进行了研究.本文讨论下承式钢桁结合梁桥在畸变荷载作用下(图2(c))的近似解析解.为简化分析,将下承式钢桁结合梁桥根据变形特征等效为连续结构,即闭口薄壁箱形结合梁(下翼缘为混凝土板).连续化处理的具体方法见文献[8].

图1 下承式钢桁结合梁桥纵梁处反对称荷载的分解Fig.1 Decomposition of antisymmetric load in longitudinal beam of the through composite truss beam

图2 下承式钢桁结合梁桥下弦结点处反对称荷载的分解Fig.2 Decomposition of antisymmetric load in bottom chord joint of the through composite truss beam
1 下承式钢桁结合梁的畸变分析
以下承式钢桁结合梁桥的等效闭口薄壁箱形结合梁为对象进行分析,其中:下标 u,h和 c分别表示等效箱形结合梁截面的上翼缘、腹板和下翼缘(混凝土板).
在畸变荷载(图2(c))作用下,横向框架将发生框架平面内的变形(即畸变),产生畸变应变能.同时,横向框架中各板也将发生顺桥向的翘曲变形,产生畸变翘曲应变能.下面先推导相应的应变能表达式,再用能量变分原理确定结构的畸变效应.

图3 横截面框架畸变模型和弯矩图Fig.3 Moment figure and distortion model of transverse section frame
1.1 横截面框架畸变应变能
为简化计算,引入如下假定:
1)横截面上正应力和剪应力沿壁厚是均匀分布的;
2)不考虑纵横梁的影响;
3)混凝土板与下弦杆无偏心.
取顺桥向单位宽度的横向框架进行分析,因混凝土板与下弦杆没有直接相连,故将横向框架中下翼缘与主桁等效腹板的连接视为铰接,其横截面框架力学模型如图3(a)所示.用力法可求解出横向框架发生畸变位移 f时,各板的弯矩和轴力为[3]

其中:

式中:T E=E s/E c为钢与混凝土的弹性模量比;I u x和 I h x分别为上翼缘(12杆 )和腹板(13,24杆)对 x轴(顺桥向坐标)的惯性矩;A c为下翼缘(34杆)的截面积;H,B为等效箱形结合梁的高度和宽度;N c为混凝土板的轴力;M 13,M 21为上翼缘的弯矩(弯矩图见图3(b)).
横截面框架畸变应变能为

其中:

1.2 横截面畸变翘曲应变能
除上述确定横截面框架畸变应变能所引入的三个假定外,再引入两个假定:
1)各板横截面法向位移沿截面周边线性分布;
2)只考虑各板在顺桥向的面内弯曲变形.
取顺桥向单位宽度的封闭框架进行分析,其力学模型见图4(a).
由假定 1)横截面上各板的应力分布规律(图4(b))及对 z轴的力矩平衡条件可得
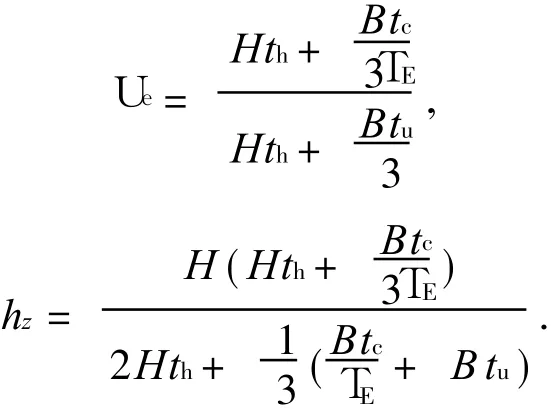

图4 横截面框架畸变翘曲模型Fig.4 Warpagedistorsion model of transverse section frame
由上翼缘的应力弯矩关系、混凝土板的应力弯矩关系以及腹板的竖向弯曲变形的应力弯矩关系可得

式中:Iuz和 Icz分别为上翼缘和下翼缘对 z轴的惯性矩;Ihy为腹板对 y轴的惯性矩.利用以上关系可得横截面框架畸变翘曲应变能

其中:

1.3 畸变控制方程
结构总势能为

令变分W∏=0,得下承式钢桁结合梁的畸变控制方程

和边界条件
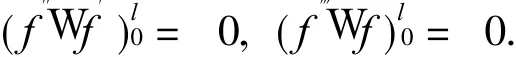
上式的通解为

待定常数 c1~ c4由边界条件确定.
2 算例及分析
某跨度为 64 m的下承式钢桁结合梁桥构造和基本尺寸如图5所示.主桁共 6个节间,桁高12.8 m,主桁中心距 15 m.混凝土板厚 27 cm,全部横梁和纵梁都为Ⅰ 字形截面,横桥向设两片纵梁,中心距为 6.5 m.钢的弹性模量 E S=2.1×105MPa;混凝土的弹性模量 E C=3.5×104MPa.结构受到的荷载为单线活载 (中-活载),相应的畸变荷载为 p=80.6 k N/m.主要计算结果见图6~图7和表1.主桁各部分杆件和节间按照由端部向跨中由小到大的顺序编号.表1中的结果仅为畸变荷载向下侧的主桁轴应力,根据对称性,另外一侧的主桁轴应力与此沿横桥向反对称分布(即对应杆件轴应力大小相等,符号相反).由上可见:
1)该桥的最大畸变位移为 12.6 mm,约为在双线对称活载作用下主桁最大挠度[7]的 1/3.
2)主桁的应力水平较低,最大应力值仅为 10.28 M Pa,变化趋势与畸变位移相吻合.
3)混凝土板顺桥向正应力,沿横桥向板端最大,正中为零.绝对值顺桥向由桥端向跨中逐渐增大,最大拉压应力为±1.09 MPa,该应力水平与双线对称活载作用下的相当.

表1 主桁 (单侧)轴应力表Tab.1 Axial force on main truss(single side)

图5 简支下承式钢桁结合梁桥(mm)Fig.5 Through steel-truss composite beam with simple-supportion
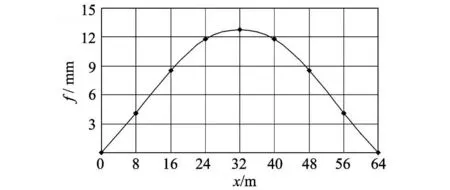
图6 畸变位移曲线Fig.6 Distorsion displacement curve
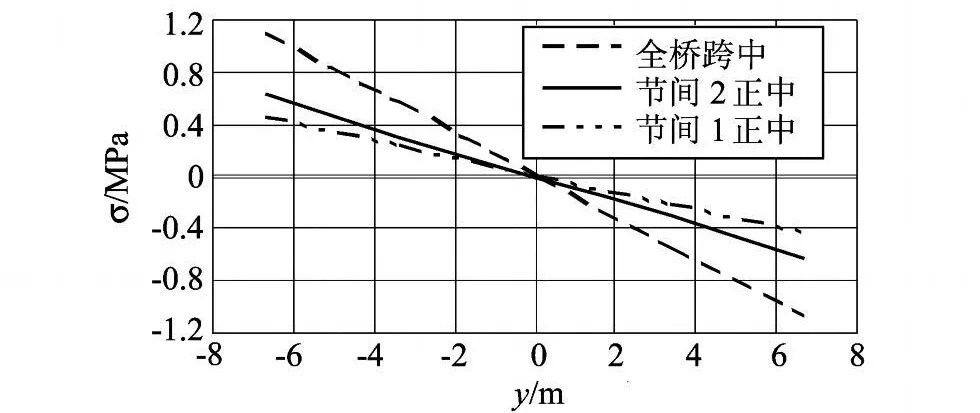
图7 混凝土板顺桥向正应力Fig.7 Normal stress of concrete slab along bridge
3 结束语
本文基于能量泛函变分原理,研究了下承式钢桁结合梁桥在畸变荷载作用下的受力特性,其结果可为这种桥型在偏载作用下的计算提供铺垫,也可为其设计提供参考.本文简化模型的思路可推广用于类似桥梁的近似计算.
[1]何畏,李乔.板桁组合结构体系受力特性及计算方法研究[J].中国铁道科学,2001,22(5):65-72.He Wei,Li Qiao.Study on features of forcebearing of plateand truss compositestructure system and thecalculation method[J].China Railway Science,2001,22(5):65-72.(in Chinese)
[2]谭莹,田启贤.板桁组合结构的受力特性及空间分析方法[J].铁道建筑,2001(8):2-5.Tan Ying,Tian Qixian.Features of force bearing and method of spatial analysis of plate and truss composite structure[J].Railway Construction,2001(8):2-5.(in Chinese)
[3]Josef Machacek,Martin Cudejko.Longitudinal shear in composite steel and concrete trusses[J].Engineering Structures,2009,31(6):1313-1320.
[4]Nie Jianguo,Tian Chunyu,Cai C S.Effective width of steel-concrete composite beam at ultimate strength state[J].Engineering Structures,2008,30(5):1396-1407.
[5]Kim H Y,Jeong Y J.Steel-concretecomposite bridge deck slab with profiled sheeting[J].Journal of Constructional Steel Research,2009,65(8-9):1751-1762.
[6]陈玉骥.下承式钢桁结合梁桥在纯扭转荷载作用下的近似解析解[C].广州:全国桥梁学术会议论文集,2007.
[7]陈玉骥.下承式钢桁结合梁在双线对称荷载作用下的近似解[J].铁道学报,2008,30(1):48-52.Chen Yuji.Approximate solution of through steel-truss composite beams under theaction of double-track symmetry loads[J].Journal of the China Railway Society,2008,30(1):48-52.(in Chinese)
[8]陈玉骥.高速铁路下承式钢桁梁-混凝土结合桥的计算理论及其应用[D].长沙:中南大学,2004.

