横向荷载作用下桩-土耦合系统的土弹簧刚度✳

曾庆敦,甄圣威

(华南理工大学土木与交通学院,广东 广州 510640)

0 引 言

随着现代科技的进步,大型建设工程的兴建,桩基础所受的水平荷载也越来越大,校核桩顶位移和土体抗力的必要性也凸显出来.但由于岩土材料本身本构关系的复杂性,以及桩-土耦合结构接触面上应力分布的复杂性,导致使用有限元软件很难模拟出这种耦合结构的实际情况.土弹簧法是工程中的一种常用方法,只要选择的土弹簧个数合适,使用土弹簧的弹力来代替土体抗力就是一种切实可行且非常简便的方法,但关键问题是如何确定土弹簧的刚度系数.已知的确定土弹簧刚度系数的方法有很多,大多是假设一种水平地基反力系数与深度的关系[1-2].这些方法或者随深度线性增大(比如现行的桥梁桩基规范推荐在一定桩顶位移范围内使用的“m”法[3]),或者不随深度变化[4].p-y曲线法[5-6]是引用国外的方法,考虑了土的非线性,并且不受桩顶位移的限制,但该法在参数选取和数值计算方面都存在一定的难度,故可操作性差.这些方法在其适用范围内校核桩顶位移时都可以满足工程的精度,但由于其基于假定的土弹簧刚度并不能准确地描述桩-土之间的相互作用,故导致计算得到的桩身各处位移与实际有差异.随着有限元软件功能的完善,越来越多的学者与工程技术人员试图用这种新的途径来解决桩-土耦合的问题,但难点在于土的本构关系在软件中的定义及桩-土耦合面的处理,使得计算结果也不尽如人意.本文将在 Mindlin解的基础上[7],充分考虑地基反力系数随深度变化的规律,提出一种新的确定土弹簧刚度系数的方法.

1 Mindlin解导出位移表达式

桩在水平荷载作用下,桩土之间的相互作用力也是水平的,可视为半无限体中的点受横向荷载作用.Mindlin的位移解[7]给出了半无限体内一点受水平荷载时的位移场函数,因此在考虑横向位移时,本文采用 Mindlin的位移解.将土体视为均质、各向同性、弹性的半无限体,压缩模量为 E s,泊松比为g.建立直角坐标系,水平面为 x-y平面,沿半无限体深度方向为 z轴,如图1所示.

图1 半无限体内一点受水平集中力示意图Fig.1 Schematic diagram of a point in semi-infinite body under lateral concentrated force

图2 半无限体内矩形面受水平面力示意图Fig.2 Schematic diagram of surface load on a rectangular in semi-infinite body

当土中 z轴上任一点(0,0,c)作用集中力 P时,由 Mindlin公式[8]可以得到土体内的位移场函数

式中:G为土的剪切模量,且

当在 x=0处的 y-z平面内一块 y=±b0/2,c=c1和 c2的矩形面 Ⅰ ,Ⅱ ,Ⅲ ,Ⅳ 上作用平行于 x轴的均布荷载 p时(见图2),y-z平面内任一点 A(0,y,z)处产生的平行于 x轴的位移可由式 (1)积分得到.该积分由 Douglas等人求出[8],本文不列出位移场函数,而直接给出由它推导的矩形面积角点Ⅰ,Ⅱ ,Ⅲ ,Ⅳ 处的位移函数.

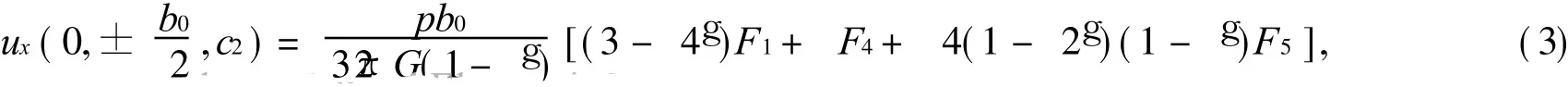
式中:F1～F5均为无量纲影响系数.

其中:

只需给出半无限体中如图2所示放置矩形的上、下边标高 c2,c1和宽 b0,代入式(6)中,将得出的K 1,K 2代入式(5)得出无量纲影响系数 F1～ F 5,再分别代入式(3)和式(4),即可解出矩形 4个角点的位移.由于边界和载荷都是关于z轴对称的,故Ⅰ和Ⅱ的位移、Ⅲ和Ⅳ的位移分别相等.

2 土弹簧刚度的确定

不考虑土的非线性特征,可视土体为弹性半无限体,于是面积 S在均布荷载 p作用下产生的土体抗力(面力)可以用弹簧弹力(集中力)来代替.将一块较大的面积分成数个较小面积,则小面积上的面力可以近似地看成均布荷载,并用弹簧弹力代替.如此,大面积上不均匀分布的面力便可离散为数个集中力.问题是如何确定这一个个离散的弹簧的弹簧刚度,显然弹簧的弹力是土体抗力在面积 S上的积分,那么关键就是如何确定弹簧的变形量Δx.

2.1 弹簧变形量的讨论

式(3)～ (6)给出的是一块矩形面在均布载荷作用下的角点位移,可将此 4个角点位移的平均值作为计算土弹簧刚度值时的参量.作用在矩形面上的均布荷载为 p,矩形的面积为 S.若将面力作用替换为等效的弹簧集中力作用,则集中力

图3 Mindlin解所用的模型及变形与桩土实际变型模Fig.3 Model and deformation used in Mindlin′s method and the actual deformation model of pile-soil coupling system

将面力替换为等效集中力后,根据弹簧刚度的定义,有了作用在弹簧上的力 f,只要知道在此力下的弹簧变形量Δx,即可由定义直接得出弹簧刚度.但弹性力学没有给出直接求此变形量的方法,因此本文认为可以在 Mindlin解的基础上加以修正,间接得到Δx.下面就此问题加以讨论:问题是可否将由式(3)～ (6)得出的 ux直接作为弹簧在 f作用下的变形量,用以计算弹簧刚度?

首先,当面积 S上作用均布荷载 p时,面 S上各点的位移是不均匀的(见图3(a)).在矩形上,4个角点的位移是最小的,矩形中心处的位移达到最大,这一点容易证明.因此,用角点位移的平均值 ux来做弹簧变形量Δx,显然会导致Δx值偏小,最终得到的弹簧刚度值偏大.

其次,Mindlin解所用的模型如图3(a).当矩形面积受到沿 x方向水平均布载荷 p作用时,变形如图3(a)中右侧粗曲线所示.面 S一侧(受载面)受到均布荷载作用,另一侧受到弹性体的抗力(压力).此外,由于面 S的受载侧并没有与弹性体发生脱离,弹性体对它仍有约束作用,故受载面上还受到弹性体对它的拉力.可能看出,矩形面积在均布荷载作用下,基于 Mindlin解推出的半无限体位移场是连续的,面 S的两侧分别受到拉力与压力的作用,面 S两侧处弹性体上点的位移与面 S上对应点的位移相同.

但实际上桩土的接触面上并不能承受上述的拉力,一旦拉力大于零,桩与土便发生脱离(其模型如图3(b)所示),不会有拉力来约束 S面的位移.那么在载荷条件相同的情况下,因为约束条件的不同,位移不连续时的角点位移比位移连续时的位移要大,即 u′x＞ux.

综上所述,由 Mindlin解导出的矩形角点位移比弹簧的变形量Δx要小.直接取 ux作为弹簧在 f作用下的变形量计算出来的刚度会比实际的要大.

2.2 弹簧刚度的确定

利用有限元软件 ANSYS,角点平均位移可通过建立图3(a)所示的数值模型求得.变形量可以将上述模型的 S面改成刚性面,刚性面位移即为变形量.通过大量有限元分析对比发现,角点平均位移 ux与变形量Δx之间存在线性关系,且系数 m取π时能够得到较为合理的刚度值

联立式(7)和式(8),则土弹簧刚度值为

桩的长度一般要比宽度大很多,因此通常将桩沿长度方向分成若干等份,每份桩对应的土体用一根弹簧代替,那么在计算每根弹簧的刚度时都需要历经式(3)～(9)的复杂计算.若需要计算的弹簧刚度系数较多,则手算将异常困难.本文使用 M ATLAB软件编制程序,实现了有限长桩等距插入任意个数弹簧后每根弹簧刚度的计算.

3 Boussinesq解导出的弹簧刚度

一个土弹簧在集中力 X的作用下,则分布于面积 b×d上的均布压力为 q=X/(bd),由 Boussinesq解可得在集中力 X作用下的位移Δ[4,8]

则

式中:k是一个与 d/b有关的形状系数,当 d/b=1时,k=0.88.在靠近地表附近的弹簧,由于边界条件的影响,其刚性系数应乘以 2/3.假定各土层条件均相同,取土的压缩模量 E s=10 MPa,泊松比g=0.3,以桩径 d=0.8 m,桩长 l=32 m的弹性长桩为例,将桩等分成 40份,即用 40根弹簧代替土体抗力.比较 Mindlin解导出的弹簧刚度与 Boussinesq解导出的弹簧刚度,将尺寸与材料属性数据代入式(10),可得 K B=999 k N/m.

4 算例分析

以混凝土灌注桩为例.土的压缩模量、泊松比、桩径、桩长的取值与前述相同,仍将桩等分成 40份,与每份桩对应的土体用一根弹簧代替,则每根弹簧代替的土体面积为 0.8×0.8 m2.弹簧顶端及桩底为简支,桩顶施加横向荷载,如图4所示.

按 Boussinesq解导出的弹簧刚度为:K 1=K2=666 k N/m,K3=…=K40=999 k N/m.按Mindlin解导出的弹簧刚度如图5所示,图中也给出了两种方法所得结果的比较.

使用 ANSYS软件建立桩-土耦合结构的梁单元与弹簧单元模型,施加 20 k N的水平荷载,得到在两种刚度条件下桩身各段处位移,如图6所示.

图4 模型示意图Fig.4 Sketch map of model

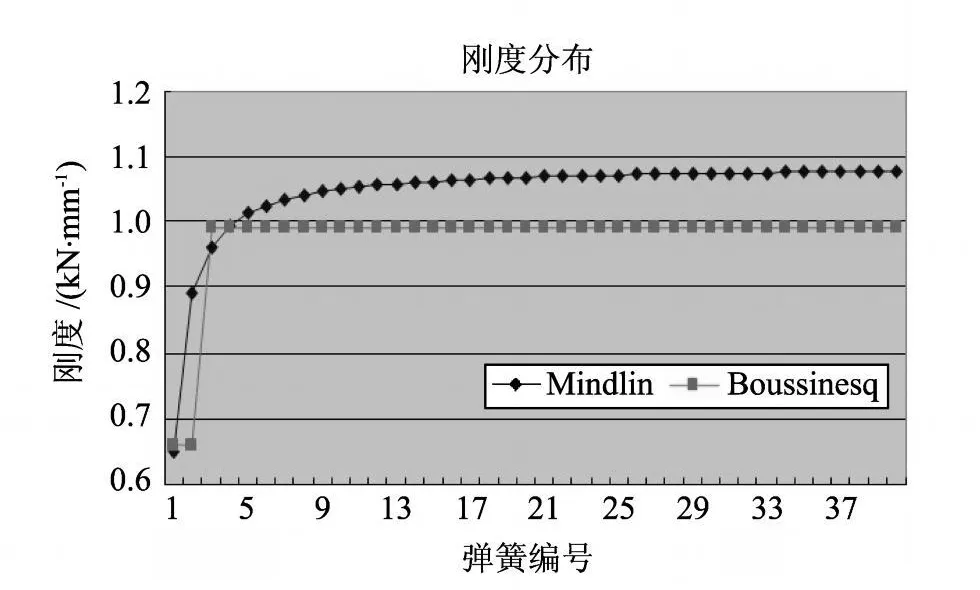
图5 两种弹簧刚度分布比较图Fig.5 Schematic diagram of comparison between two kinds of spring stiffness coefficients

图6 两种弹簧刚度下桩身各段处的位移比较Fig.6 Comparison of displacements at each sections in pile body under the condition of two kinds of spring stiff ness coefficients

由图5可以看出,由 Boussinesq解导出的刚度除在地面附近处乘以 2/3的系数外,其余都相等.而在实际上随着深度的增加,地面边界条件对地基反力系数的影响会越来越小,故弹簧的刚度系数是递增的,此为其一.其二,由于地面边界条件的影响不会延伸到无穷深处,故地基反力系数也将收敛,即弹簧的刚度系数会随着深度的增加而逐渐趋于稳定.分析发现,如果考虑上述桩为无限长桩,则弹簧刚度将收敛于 1 085.2 k N/m.其三,由图5可知,基于 Mindlin解导出的弹簧刚度较大,它的收敛值要比Boussinesq解导出的刚度大 8.6%.这仍然是由于边界条件的不同而引起的,后者将桩土作用力简化为作用在半无限体表面上的面力,仅仅考虑受载面某一侧的土体变形;而前者则考虑了受载面两侧所有土体的变形,与实际的桩-土耦合结构模型更加接近.这一点很容易理解,两种模型下,参与变形的土体越多,那么相同位移条件下,土体存储的应变能将越多,也就是说需要的外力功越多;由于位移相同,显然所需要的力更大,即刚度更大.出于对边界条件的考虑,本文认为由 Mindlin解导出刚度系数更加合理.由图6可见,两种方法得出的位移结果非常接近,Mindlin解导出的位移(绝对值)要略小,差别最大处仅为3.97%.

由于本文没有考虑土的非线性特征,因此计算结果还无法与现行的非线性计算方法(如 NL法等)相比较;其次,本文仅考虑弹簧所代替的土体面积为矩形,并没有考虑面积形状任意时的情形.

5 结束语

本文的主要工作和结论体现在以下两个方面:

首先,土弹簧刚度系数是由地基反力系数乘以弹簧所代替土体的面积直接换算而来的,而其他文献中所介绍的确定地基反力系数方法大多是建立在假设地基反力与深度的关系的基础上.本文分析了桩-土耦合结构模型,基于对边界条件的考虑,认为使用 Mindlin导出的位移解能更准确地反映地基反力系数随深度的变化规律.其次,本文的关键结论是得出了计算土弹簧刚度时位移参量的求法,即在矩形 4个角点位移的平均值的基础上乘以常数,并通过 MATLAB编程的方法实现了任意长度及直径桩、任意等分后弹簧刚度的计算.通过算例的分析可以发现,这样算出的弹簧刚度是准确的,也验证了本文在确定位移参量时选取系数π的合理性.

[1]彭明祥,毛艳荣.深基坑桩墙支护结构数值分析实用方法[J].建筑结构,2001,31(4):37-40.Peng Mingxiang,Mao Yanrong.Practical method for numerical analysis of pile wall retaining structure in deep foundation pit[J].Building Struct,2001,31(4):37-40.(in Chinese)

[2]王春,王宏东.桩-土作用模型在桥梁设计中的研究与应用 [J].工程与建设,2007,21(5):770-772.Wang Chun,Wang Hongdong.Study and application of soil-pile function model in bridge design[J].Engineering Construc,2007,21(5):770-772.(in Chinese)

[3]中华人民共和国交通部.公路桥涵地基与基础设计规范(JTG D63-2007)[S].北京:人民交通出版社,2007.

[4]陆培炎.陆培炎科技著作及论文选集 [M].北京:科学出版社,2006.

[5]王成华,孙冬梅.横向受荷桩的 p-y曲线研究与应用述评[J].中国港湾建设,2005(2):1-4.Wang Chenghua,Sun Dongmei.Review of the researches and applications of p-y curves for laterally loaded piles[J].China Harbour Engineering,2005(2):1-4.(in Chinese)

[6]洪勇,谢耀峰,张圣平,等.水平荷载下单桩有限元模拟结合 p-y曲线法分析[J].中国港湾建设,2007(3):5-9.Hong Yong,Xie Yaofeng,Zhang Shengping,et al.Analysis of single pile under lateral loads with simulations by fem in combination of p-y curve approach[J].China Harbour Engineering,2007(3):5-9.(in Chinese)

[7]左名麟,胡人礼,毛洪渊.桩基础工程[M].北京:中国铁道出版社,1996.

[8]SOIL M ECHANICSWork Team at Hohai University.Soil Mechanics[M].北京:人民交通出版社,2004.