自锚式斜拉-悬吊协作体系桥静风响应分析

陈 国 芳, 张 哲＊, 吴 宏 业, 谭 岩 斌

(1.大连理工大学土木工程学院,辽宁大连 116024;2.辽宁省交通勘测设计院,辽宁沈阳 110005)

0 引 言

目前世界上采用的大跨桥型是斜拉桥和悬索桥,因其具有受力合理、外形美观、跨越能力强等优点,在我国大江大河上得到了广泛应用.随着我国国民经济和交通事业的迅猛发展,在沿海地区即将或已经修建了跨海大桥,然而这些桥梁工程不可避免地受软土地基、深水基础、强台风等自然因素的影响,因此仅选用斜拉桥和悬索桥可能不满足工程需求.而斜拉-悬吊协作体系桥(简称协作体系桥)是在传统悬索桥和斜拉桥基础上发展起来的一种新型的组合结构型式桥梁,它克服了单一悬索桥和斜拉桥在力学性能、施工以及抗风稳定性等方面的不足,具有较强的跨越能力.因此,斜拉-悬吊协作体系桥为这些跨海工程的实施提供了一种比较合理的解决方案.在桥梁加固方面,一些悬索桥如法国的Tancarville桥和葡萄牙的Salazar桥都采用这种体系;而在设计方面,许多跨海大桥如丹麦的大贝尔特东航道桥、直布罗陀海峡桥、土耳其的Izmit桥以及日本的轻津海峡桥等也采用了协作体系.在我国,设计伶仃洋跨海大桥时,同济大学和重庆交通学院都提出了跨径超过千米的斜拉-悬吊体系桥的设计方案.1997年10月我国贵州的乌江大桥竣工通车,标志着世界上首座现代化斜拉-悬吊协作体系桥的诞生.

目前协作体系桥主要停留在方案的设计阶段,且均为地锚体系,这就需要设计和建造庞大的锚碇,施工难度大、工程造价高.但是如果采用自锚体系,不但可以节省锚碇,而且将缩短工期.大连市庄河建设大桥就采用自锚式斜拉-悬吊协作体系,大大节省了工程造价,取得了良好的经济效益.协作体系在设计和建造过程中有许多技术难题有待深入研究.这些难题包括静动力性能、经济性能、抗风稳定性等.文献[1～3]在协作体系的力学性能和经济性能方面进行了研究.文献[4、5]对协作体系分别从悬索的矢跨比、吊跨比、斜拉索索面的布置形式、桥面主梁构成以及边跨辅助墩的设置等设计参数着手,进行了颤振稳定性分析,从中得到了一些有意义的结论,并从抗风性能角度探讨了斜拉-悬吊协作体系桥的合理结构型式.文献[6～8]分析了自锚协作体系的静动力特性,并阐述了吊索的疲劳问题.文献[9]研究了结构几何非线性、侧向气弹效应、气动导纳、自然攻角及缆索上脉动风等对自锚协作体系抖振的影响,并特别指出缆索上的脉动风引起了主缆的振动并与主梁产生耦合振动.自锚协作体系通常建造在台风频发的地区,而且随着其跨径的增大,抗风稳定性问题将更加突出.因此,有必要对自锚协作体系的抗风稳定性能进行分析研究.本文以主跨为400 m的大连金州海湾大桥的方案设计为工程背景,研究自锚式斜拉-悬吊协作体系桥在静风作用下,桩基础刚度、拉索分段、初始攻角、附加攻角等对主梁和桥塔静风位移的影响,以期为将来进行三维非线性颤抖振分析奠定基础.

1 大连金州海湾大桥总体布置及有限元模型建立

1.1 方案桥布置图

金州海湾大桥方案设计为132 m+400 m+132 m的自锚式斜拉-悬吊协作体系桥,采用了修正的狄辛格体系,边跨与中跨之比为0.33∶1,边跨还设有一辅助墩.主梁竖曲线半径为10 km,纵坡为0.45%,桥面宽26 m,双向6车道;斜拉部分主梁采用钢筋混凝土材料,悬索部分主梁为钢结构.主塔为H形双独柱索塔,斜拉索采用扇形索面,设有零号索.全桥采用漂浮体系,如图1所示.

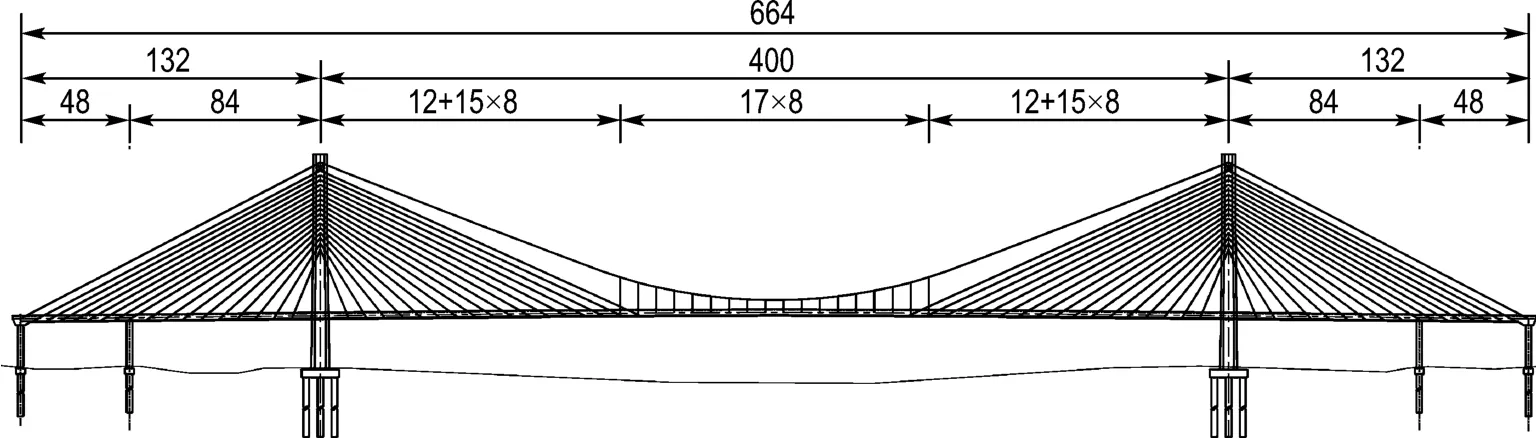
图1 金州海湾大桥方案设计布置图(单位:m)Fig.1 Schematic design layout of the Jinzhou Gulf Bridge(units:m)

1.2 空间有限元模型的建立

采用ANSYS有限元分析程序,建立了该桥的空间有限元模型.在有限元模型中,主梁采用了脊骨梁计算模型,主梁、桥塔、桥墩及横系梁采用非线性空间梁单元模拟,用空间杆单元模拟主缆、吊杆和斜拉索;边界条件为桩底固结,主梁和桥塔之间无纵向约束但有侧向约束,主缆锚固在边墩上.由于该桥的断面和苏通大桥的断面形状比较相似,虽然缺乏该桥的节段模型风洞试验数据,但可以采用苏通大桥主梁节段模型试验测得的静三分力系数[10](见图2)进行静风响应分析.

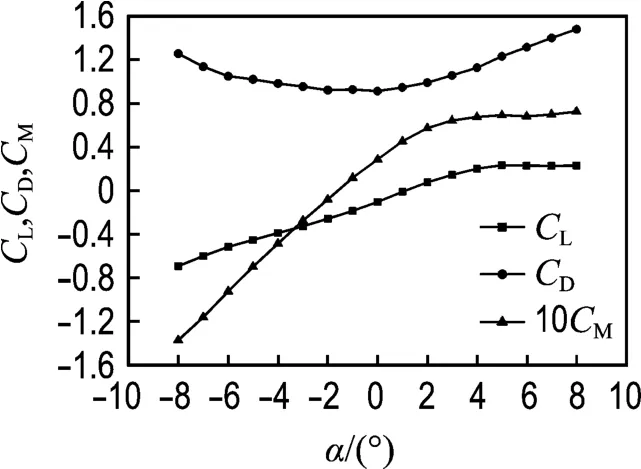
图2 主梁断面静三分力系数Fig.2 Aerostatic coefficients of bridge deck section

2 静风响应的计算模式和分析步骤[11、12]

在金州海湾大桥静风响应分析中,为了分析桩基础对结构静风响应的影响,边界条件采用考虑和不考虑桩基础刚度两种;在分析不同初始攻角下的结构静风响应时,初始攻角采用-5°、-3°、0°、3°和 5°五种;针对主梁附加攻角对结构静风响应的影响,附加攻角取为考虑和不考虑附加攻角两种方式;为考虑斜拉索的影响,斜拉索采用多分段(统一等分为10段)和单一段两种计算方式;为了分析缆索体系的风荷载在总体风荷载中所占比例,缆索系统风荷载取为考虑和不考虑缆索体系风荷载(缆索体系包括主缆、斜拉索、吊杆)两种方式.

静风作用下的桥梁结构位移响应及静风失稳风速基于ANSYS通用有限元软件计算,如图3所示,采用以下步骤进行求解:

(1)在结构自重荷载作用下,进行线性求解.

(2)在ANSYS中以table形式存储桥梁主梁断面的静三分力系数,给定某级风速及初始攻角,从table中提取对应的静三分力系数;按照规范确定主塔、桥墩及缆索的阻力系数,将与这些系数相关的风荷载添加到有限元模型中.

(3)对桥梁结构进行非线性有限元静力分析,提取主梁节点扭转角,根据不同攻角(初始攻角+附加攻角)时主梁的静三分力系数重新计算主梁风荷载.

(4)循环迭代直至达到一定次数或相邻两次计算位移响应(线位移或扭转角)之间差值的某种范数小于某允许值,此时可以确定该级风速时的结构位移响应.

(5)增加风速到下一级,最好是有规律地逐级增加,以便进行计算,重复步骤(2)～(4),如果非线性分析结果收敛,可以确定该级风速时的结构位移响应;如果非线性分析出现迭代不收敛,则减小风速重新分析,结合内插法可以足够准确地确定静风失稳风速.

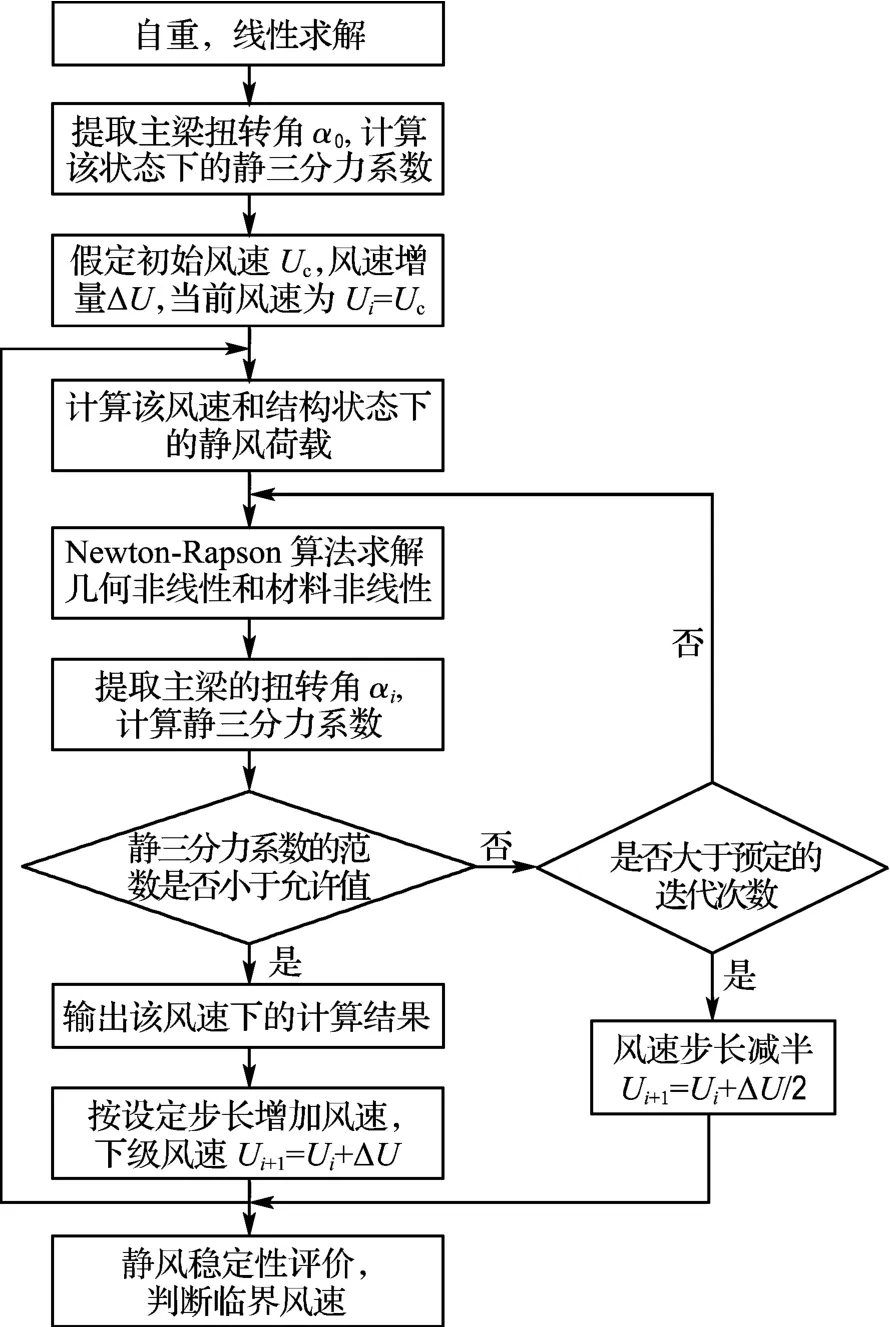
图3 非线性静风稳定流程Fig.3 The flowchart of the nonlinear static stabilization

3 自锚式协作体系的静风位移

3.1 初始攻角的影响

分别考虑了桩基础刚度和斜拉索多分段建模的影响,金州海湾大桥在设计基准风速作用下,不同初始攻角各种计算模式对应的主梁跨中断面的竖向、侧向和扭转位移,塔顶沿桥纵向、侧向和绕竖向扭转位移变化曲线分别如图4～9所示.

由图4可见,主跨主梁竖向位移随着初始攻角的增大而增大;主梁先被下压然后慢慢抬起,其原因是图2中的升力系数CL由负变正;由于边跨的跨径较小而且有辅助墩,边跨主梁的竖向位移随攻角变化不明显,且远远低于主跨主梁位移.图5表明随初始攻角的增大主跨主梁侧向位移也增大,且边跨主梁的侧向位移远小于主跨主梁位移,在主塔处存在拐点.从图4和图5的位移可以看出,主梁作类似固定在塔顶的单摆运动,侧向位移随着主梁位置的抬高而增大.由图6可以看出,跨中扭转位移随初始攻角的增大而减小.从图7可以得到,随着初始攻角的增大,塔的水平位移由初始的向跨中倾斜慢慢地变成向边跨倾斜,与图4显示的主梁竖向位移相协调,满足结构变形的相容条件.由图8和图9可知,初始攻角对主塔的侧向位移和扭转位移影响相对较小,扭转位移出现拐点的主要原因是两塔柱之间横梁的刚度约束了主塔的扭转位移.

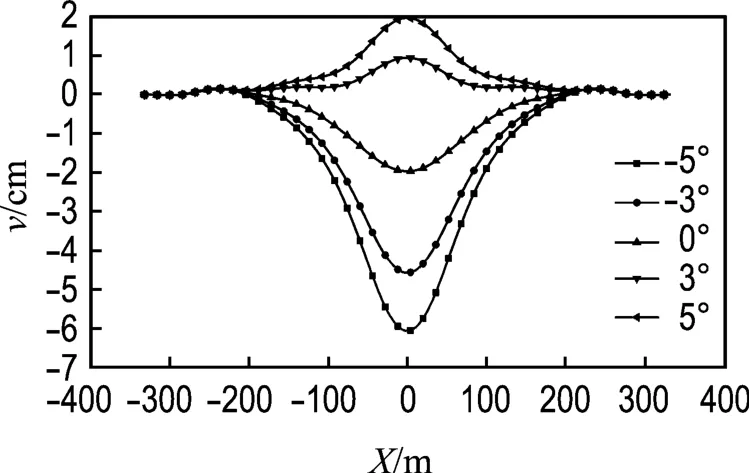
图4 不同初始攻角下的主梁竖向位移Fig.4 Vertical displacements of main girder with various initial attack angles

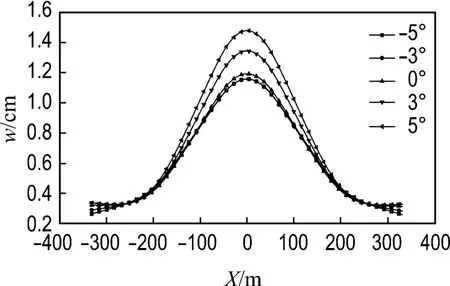
图5 不同初始攻角下的主梁侧向位移Fig.5 Lateral displacements of main girder with various initial attack angles

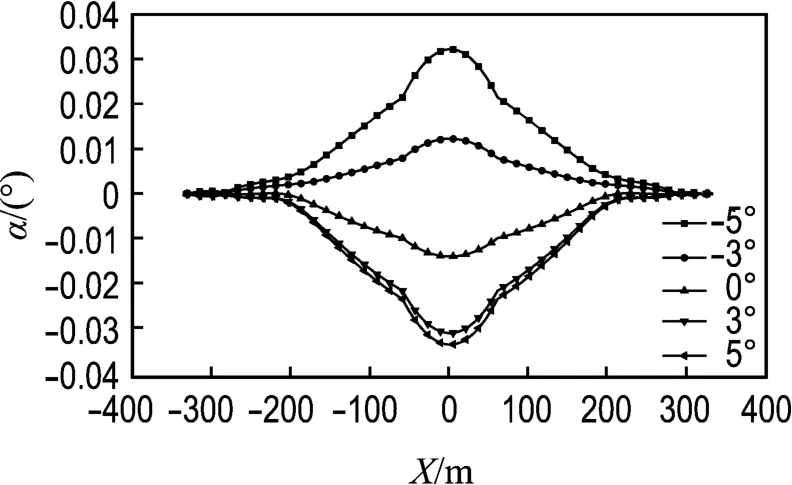
图6 不同初始攻角下的主梁扭转位移Fig.6 Torsional displacements of main girder with various initial attack angles

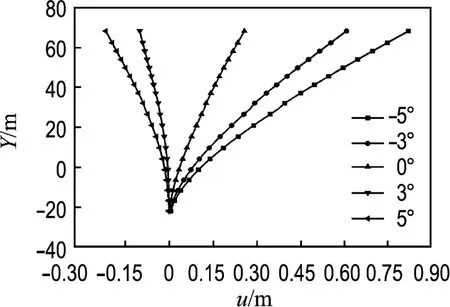
图7 不同初始攻角下主塔水平位移Fig.7 Longitudinal displacements of main pylon with various initial attack angles

3.2 缆索体系风荷载的影响

为了计算缆索体系风荷载占总体侧向风荷载的比例,对是否计入缆索体系风荷载进行了对比分析.由于缆索体系的风荷载主要影响桥塔和主梁的侧向位移 ,本文只给出了-3°、0°和 3°三种不同初始攻角下相应的侧向位移响应(见图10、11).

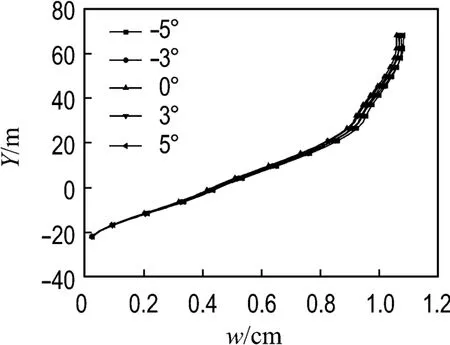
图8 不同初始攻角下主塔侧向位移Fig.8 Lateral displacements of main pylon with various initial attack angles

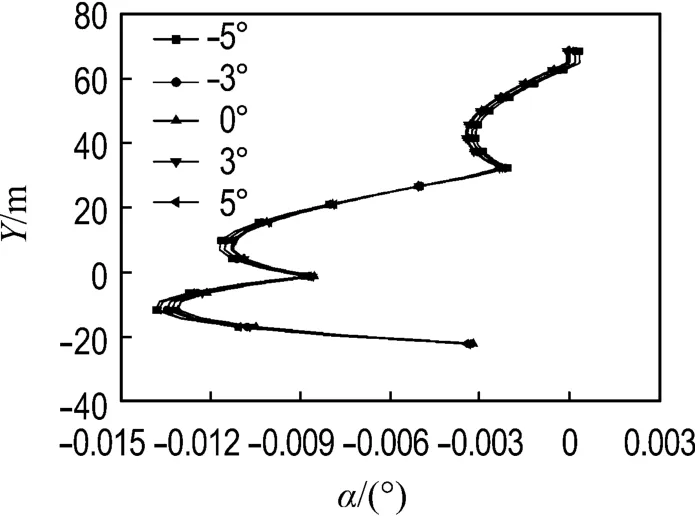
图9 不同初始攻角下主塔扭转位移Fig.9 Torsional displacements of main pylon with various initial attack angles

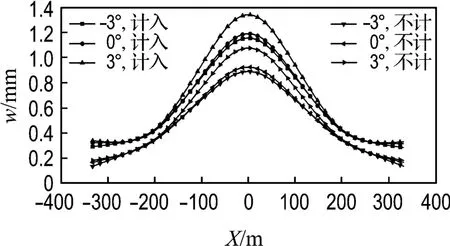
图10 计入和不计入缆索体系风荷载主梁侧向位移Fig.10 Main girder′s lateral displacements with or without cable system wind load

由此可见,缆索体系的风荷载对主梁和主塔侧向位移影响比较显著,其中对塔柱附近位移影响较小,越远离塔柱的主梁侧向位移受风荷载影响越大.为了量化缆索体系风荷载占全部风荷载的比例,表1给出了计入和不计入缆索体系风荷载的位移值,并给出其相对差值,由此可知,缆索体系的风荷载占全部风荷载的20%左右.

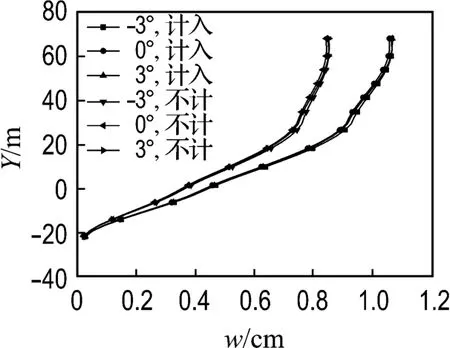
图11 计入与不计入缆索体系风荷载主塔侧向位移Fig.11 Main pylon′s lateral displacements with or without cable system wind load

3.3 桩基础和斜拉索分段的影响

为了考虑桩基础和斜拉索分段对自锚式协作体系静风响应的影响,分别建立了考虑与不考虑桩基础刚度的斜拉索分段和考虑桩基础刚度的斜拉索不分段有限元模型.图12、13给出了初始攻角0°时3种不同计算模式下主塔和主梁的侧向位移.从图中可以看出,忽略桩基础刚度的影响,将会低估主塔和主梁的侧向位移;且边跨主梁位移对桩基础刚度的影响的敏感程度大于主跨.斜拉索不分段将会严重低估主梁跨中的侧向位移;从塔柱向塔柱两侧,主梁的侧向位移被低估的程度越来越大.

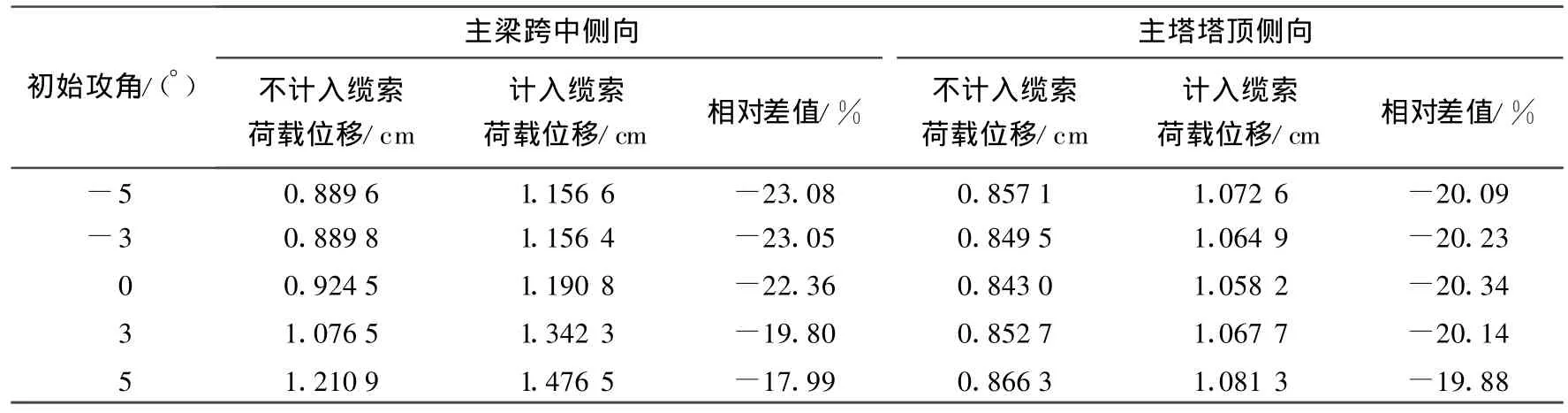
表1 缆索体系风荷载对静风位移的影响Tab.1 Influence of the cable system wind load on static wind displacement

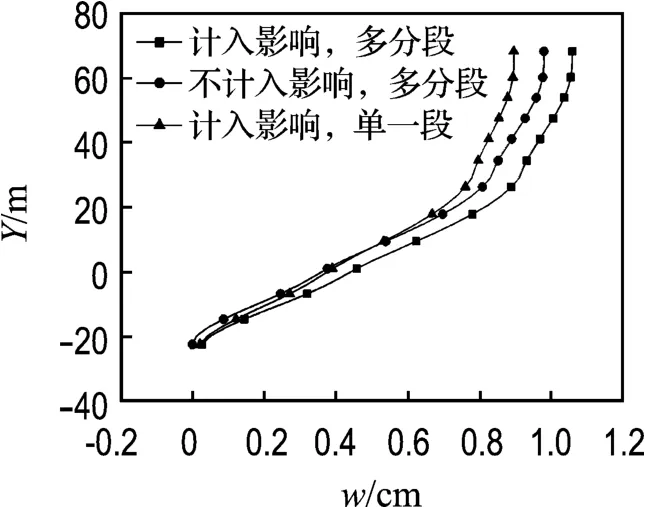
图12 桩基础刚度和斜拉索分段对主塔侧向位移的影响Fig.12 Influence of pile foundation rigidity and cable segmentation on main pylon′s lateral displacement

3.4 附加攻角的影响

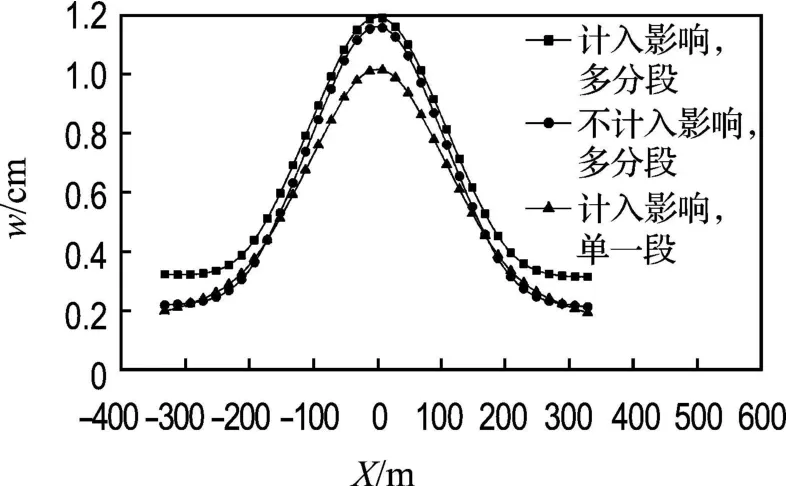
图13 桩基础刚度和斜拉索分段对主梁侧向位移的影响Fig.13 Influence of pile foundation rigidity and cable segmentation on main girder′s lateral displacement

针对附加攻角对自锚式协作体系桥静风响应的影响,结合计入和不计入附加攻角,建立了同时考虑桩基础刚度、缆索体系风荷载和斜拉索分段效应的有限元模型.表2给出了计入和不计入附加攻角时5种初始攻角工况下主梁跨中位移的大小,由表可见,附加攻角对主梁的竖向位移和扭转位移影响较小,且对主梁侧向位移的影响几乎可以忽略不计.从工程角度来考虑,该方案桥可以忽略附加攻角的影响.

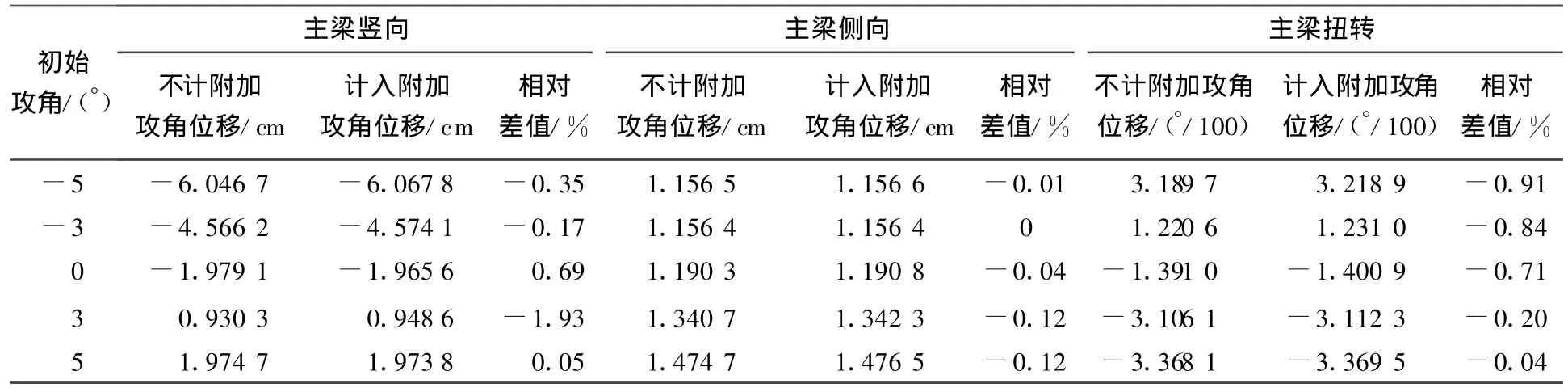
表2 附加攻角对主梁位移的影响Tab.2 Girder displacement with or without additional attack angle

4 金州海湾大桥成桥状态静风稳定分析

由文中给出的分析步骤编制了静风稳定分析程序,并对金州海湾大桥进行了非线性静风稳定的全过程分析.分别以初始攻角 3°和 0°,初始风速U0=80 m/s,风速步长10 m/s对成桥状态的金州海湾大桥进行逐级加载,直至发生静风失稳.图14、15给出了3°和0°初始攻角下主跨主梁跨中截面位移随风速变化的全过程,其中Y和N分别表示考虑和不考虑静风荷载非线性.由图14和15可见,随风速的增大,结构的竖向位移和扭转位移都以明显的非线性增长,而侧向位移有接近线性增长的趋势;静风荷载非线性对主梁的竖向位移和扭转位移影响明显,而对侧向位移几乎没有影响;桥梁的稳定性随着初始攻角的增大而下降.从图15可以看到一个特殊现象,随着风速的增大,竖向位移曲线先下降后上升,其原因是在0°附近的CL为负值,CM为正值.静风失稳形态在0°攻角下以竖向失稳变形为主,牵连着侧弯和扭转变形,仍是空间弯扭耦合失稳;而在3°攻角下是以扭转失稳变形为主的空间弯扭耦合失稳.

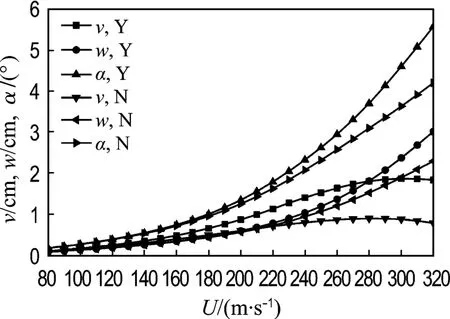
图14 跨中截面位移随风速变化全过程(初始攻角3°)Fig.14 Section displacements of midspan with wind velocity at the initial attack angle of 3°

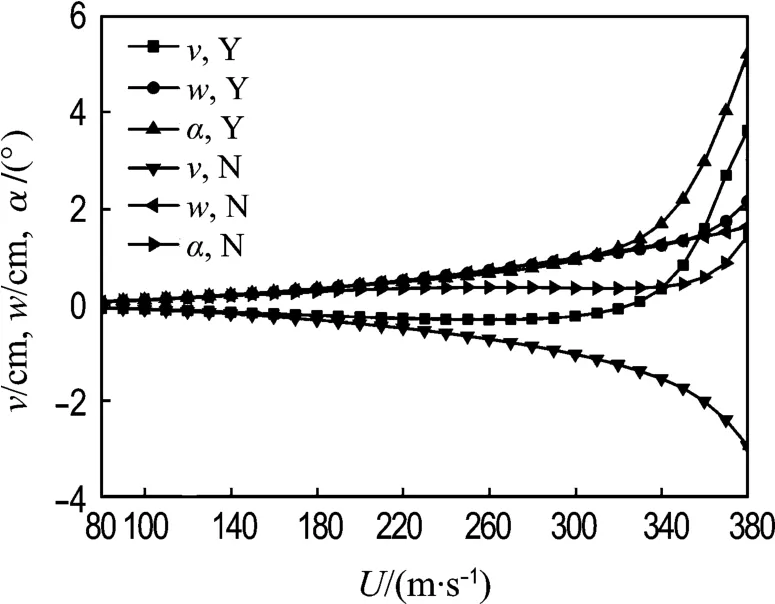
图15 跨中截面位移随风速变化全过程(初始攻角 0°)Fig.15 Section displacements of midspan with wind velocity at the initial attack angle of 0°

5 结 论

(1)缆索体系侧向风荷载在自锚协作体系下产生的侧向位移占总体位移20%左右;

(2)如果不考虑桩基础刚度的影响,将会低估主塔和主梁的侧向位移;

(3)对于金州海湾大桥而言,附加攻角对主梁位移响应的影响小于工程相对误差5%,故可以忽略不计,但是随着自锚式协作体系的跨径增大,附加攻角效应会显著加大;

(4)随着初始攻角的增大,自锚式协作体系桥梁的静风稳定性略有下降.

[1]肖汝诚,项海帆.斜拉-悬吊协作体系桥力学特性及其经济性能研究[J].中国公路学报,1999,12(3):43-48

[2]肖汝诚,贾丽君,薛二乐,等.斜拉-悬吊协作体系桥的设计探索[J].土木工程学报,2000,33(5):46-51

[3]曾 攀,钟铁毅,闫贵平.大跨度斜拉-悬吊协作体系动力分析[J].计算力学学报,2002,19(4):472-476

[4]张新军,孙炳楠,陈艾荣,等.斜拉-悬吊协作体系的颤振稳定性研究[J].土木工程学报,2004,37(7):106-110

[5]ZHANG Xin-jun,SUN Bing-nan.Parametric study on the aerodynamic stability of a long-span suspension bridge[J].JournalofWind Engineering and Industrial Aerodynamics,2004,92(6):431-439

[6]张 哲,王会利,黄才良.自锚式斜拉-悬索协作体系桥梁设计与分析[J].公路,2006,7(7):44-48

[7]黄海新,张 哲,石 磊.自锚式斜拉-悬吊协作体系桥动力分析[J].大连理工大学学报,2007,47(4):557-562(HUANG Hai-xin,ZHANG Zhe,SHI Lei.Dynamic analysis of self-anchored cable-stayed suspension bridge [J].Journal of Dalian University of Technology,2007,47(4):557-562)

[8]张 哲,杜高明,谭岩斌,等.大跨度自锚式斜拉-悬吊协作体系桥模型试验研究[J].公路交通科技,2007,24(6):75-79.

[9]黄海新.自锚式斜拉-悬吊协作体系桥动力响应研究[D].大连:大连理工大学,2007

[10]陈艾荣.苏通长江公路大桥主桥结构抗风性能研究——主桥节段模型风洞试验研究[R].上海:同济大学土木工程防灾国家重点实验室,2002

[11]吴宏业.自锚式斜拉-悬索协作体系桥静力性能分析[D].大连:大连理工大学,2007

[12]许福友.桥梁结构颤振导数识别与颤振分析[D].上海:同济大学,2006