饱和软黏土地基中单桶形基础水平承载特性有限元研究

孙 曦 源, 栾 茂 田, 唐 小 微

(1.大连理工大学海岸和近海工程国家重点实验室,辽宁大连 116024;2.大连理工大学土木工程学院岩土工程研究所,辽宁大连 116024)

0 引 言

1994年 7月,世界第一座桶形基础平台Europipe 16/11E于北海安装成功[1].它的诞生对于边际油田的开发具有重大意义,因此被挪威专家誉为“导管架基础工程技术新时代的曙光”.桶形基础在外形上多为底端开口、顶端封闭的倒扣大直径圆桶.安装时,首先依靠桶体自重使其部分地插入土中以形成密闭空间,然后抽出桶内的空气,利用内外压力差,将桶基逐步压入至海床内预定深度完成安装[2].施以其相反的过程,桶基便可从土中拔出,运送到其他海域进行循环再利用.与传统的基础形式相比,桶形基础在节省建设成本、缩短施工周期方面具有较为显著的优点,因此,桶形基础在不久的将来必然会有更为广阔的应用前景.

桶形基础在服役过程中,将承受水平荷载、竖向荷载以及弯矩的共同作用.而根据以往的实践经验可知,其中水平荷载的承受能力对于桶形基础的稳定性而言显得更为重要[3].为此,桶形基础水平承载力的确定已经成为现阶段国内外学者的研究热点.

本文利用三维有限元方法对已有的室外模型试验进行数值模拟,并对两者的结果作出比较,以验证本文有限元方法在求解此类问题时的合理性和可靠性;进而通过一系列的变动参数比较研究,得出一些有用的结论,为创立成熟的桶形基础设计理论积累一定的数值分析经验.

1 模型试验

近年来,为了更好地把握桶形基础的水平承载规律,国内学者相继开展了一系列的室内和室外模型试验研究.施晓春等[4]在距离人工海堤5 m的区域进行了室外钢质单桶模型的水平加载试验,如图1所示.主要试验参数总结如下:桶壁厚度t=5 mm,桶体直径D=0.5 m,桶体埋深L=0.5 m,室外土体的不排水抗剪强度Su=9.54 kPa,含水量 w=38.6%,浮重度 γ′=8.3 kN/m3,液性指数Il=0.82,水平荷载作用点距泥面高度Lp=0.1 m.试验采用单循环连续加载法施加水平荷载,每级加载量为预估极限荷载的1/10,每级荷载维持20 min,当基础侧面地表出现明显裂缝或隆起时,模型桶基达到极限承载状态,终止试验.由此可测得其水平承载力Ph为1.20 kN.

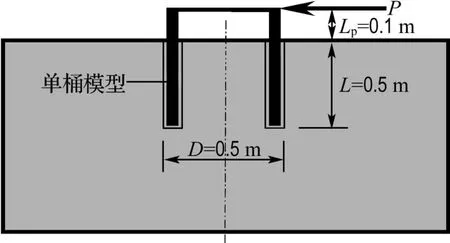
图1 室外模型试验Fig.1 Field model test

2 三维有限元法

2.1 有限元建模

本文利用大型通用有限元分析软件ABAQUS对上述室外模型试验进行三维有限元模拟.土体可视为理想弹塑性体,按照Von Mises屈服准则进行计算[5],其泊松比ν=0.49,弹性模量E分别取为300倍、500倍和1000倍的Su.桶体可视为线弹性体,其 ν=0.3,E=210 GPa.另外,为了保证在数值分析过程中应力的平衡,这里假定桶体与土体的浮重度相等[6].

考虑到试验过程中荷载及变形的对称性,仅对1/2模型进行建模,如图2所示.为了达到改善计算精度、降低计算成本的目的,有限元模型尺寸应该得到较为合理的选择.参考已有的研究成果[5]可知,当土体直径为桶体直径的10倍,土体高度为桶体高度的3倍时,边界效应对于计算结果的影响较小,可以忽略不计.有限元模型各边界的约束条件为土体底部边界竖直向约束,土体侧向边界径向约束,对称面边界法向约束.

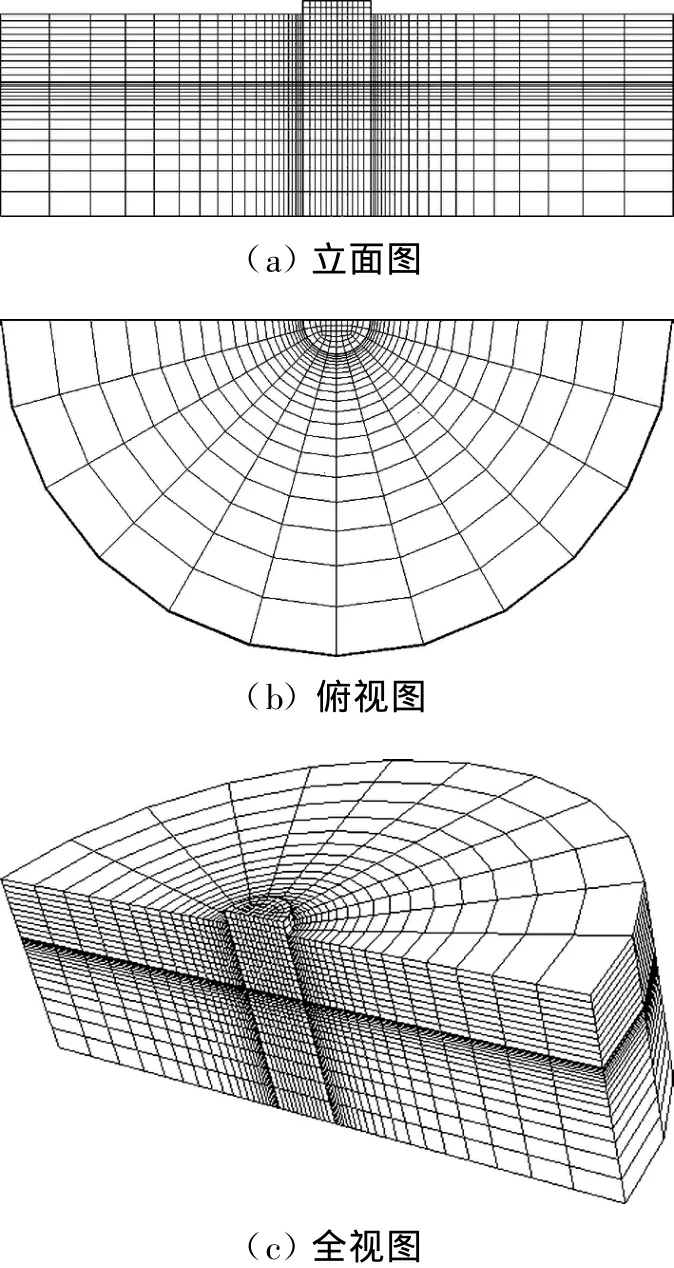
图2 有限元模型Fig.2 Finite element model

正确地处理桶土表面间的接触关系是此模拟成功的关键.在 ABAQUS中,采用主从接触对(contact pair)算法来定义该接触[7].由于桶体材料的刚度和强度显著高于土体材料,可将桶体表面选作主动面,对应的土体表面选作被动面.而在一对接触面之间,一般又同时存在两种具体的接触:切向接触和法向接触.在这里切向接触利用Coulomb摩擦定律来描述,而法向接触则采用“硬”接触(hard contact)模型进行表征,即当两接触面相互接触时,界面之间接触间隙为0,法向接触力通过主从面之间所建立的接触约束条件相互传递;当两接触面发生分离时,接触压力变为0或为拉力,主从面之间的接触约束将自动取消,界面上的摩擦力消失.通过这种设置,可以模拟桶体表面与相邻土体之间发生脱离、形成裂缝等非线性过程.

在数值分析中,位移控制法和力控制法是两种较为常见的荷载施加方法,而在实际的工程中,某一确定的泥面位移量d(0.02 D)或桶体转动角度ω(0.02 rad)往往成为桶形基础达到水平极限承载状态的判别标志.为了尽可能地使模拟过程逼近实际,这里采用位移控制法来施加水平荷载.

2.2 结果分析

由图3的对比分析可知,土体的变形模量对桶基达到极限承载状态所需施加的水平位移具有显著影响,而对桶基的水平承载力几乎不产生影响,Ph均近似等于1.13 kN,这与上述试验结果吻合较好.因此,在本文以下的研究中,土体的变形模量E统一取为300Su.

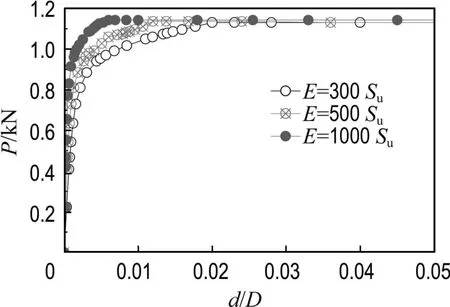
图3 不同土体变形模量条件下的荷载-位移关系Fig.3 Load-displacement responses for different modulus of soil

利用三维有限元的模拟功能,可以较为直观地得到饱和软黏土地基中单桶形基础在水平荷载作用下的破坏模式,如图4所示.从图4(a)中不难看出,当桶体达到水平极限承载状态时,主动区土体出现裂缝,被动区土体产生隆起,这与上述的试验现象较为符合.另外,从合位移矢量图中可以清晰地发现桶体绕泥面与基底之间某点发生转动,从图4(b)中可以得到该转动中心的深度z0为0.73L.图4(c)为在水平荷载作用下的泥面合位移等值线图,从中可以发现,最大泥面合位移出现在水平加载方向,并随着θ的增加而逐渐减小,在θ=π/2处,泥面合位移近似等于0.

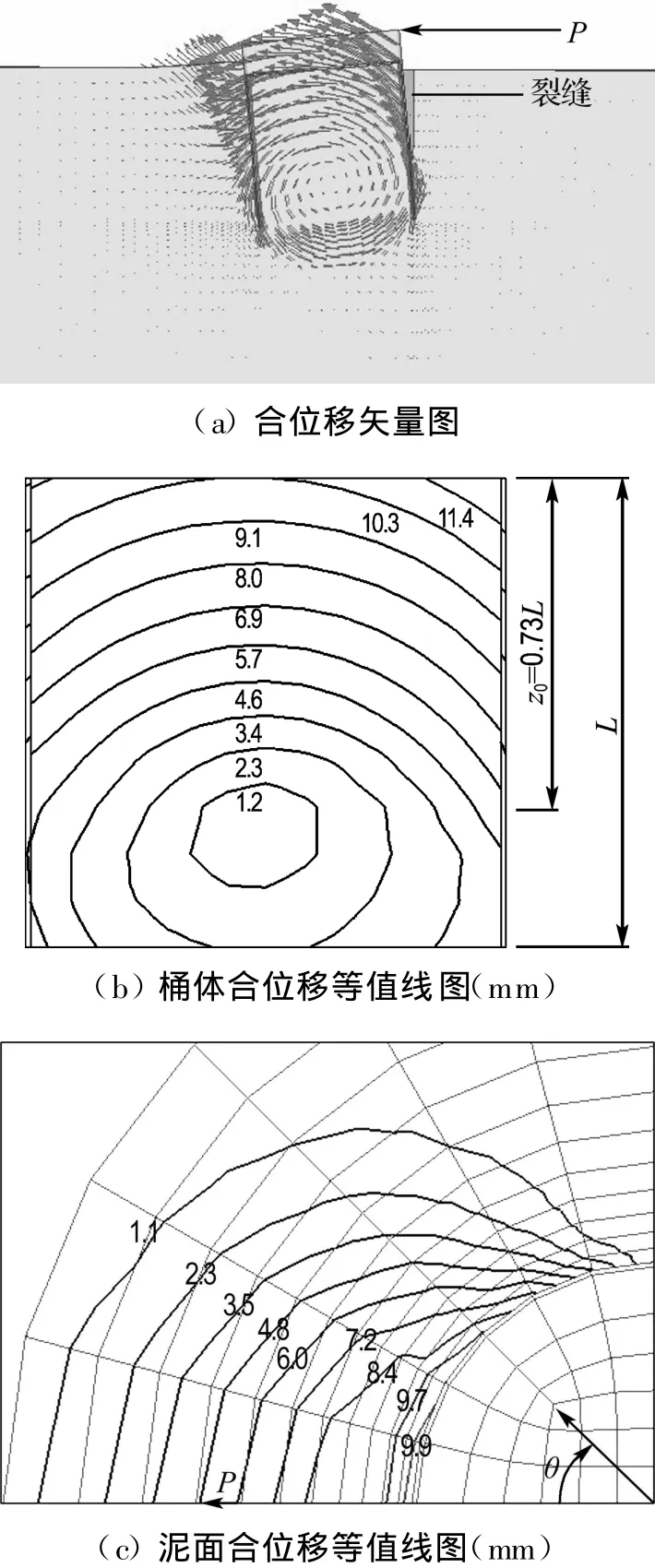
图4 有限元预测的破坏模式Fig.4 The failure mechanism predicted from FE

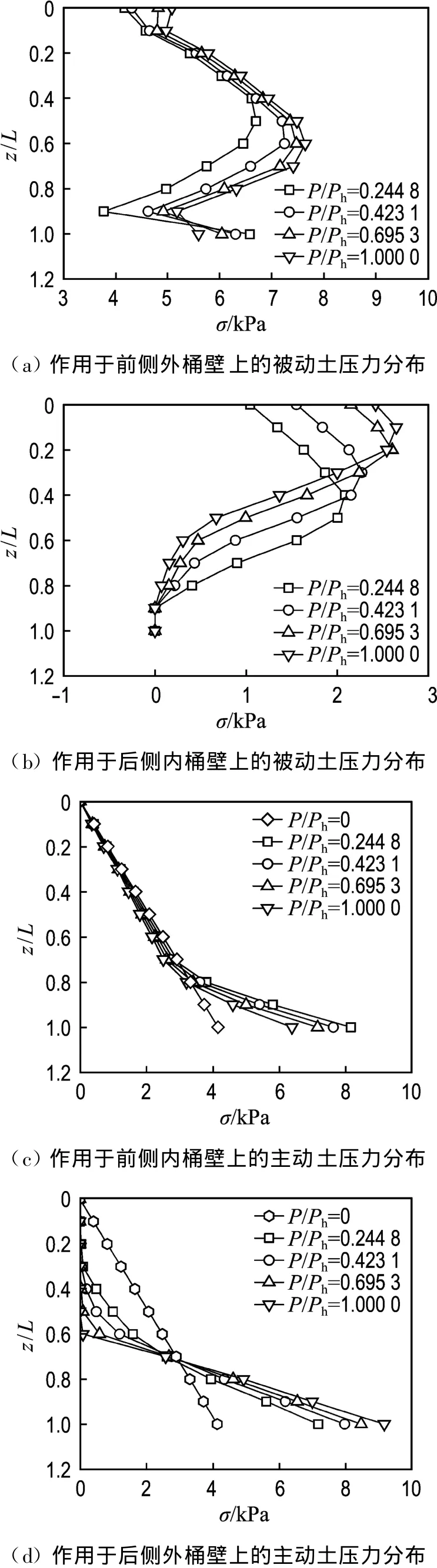
图5 不同荷载水平条件下的土压力分布Fig.5 Distribution of earth pressure on bucket surfaces for different loading levels

图5 为在不同的荷载水平条件下,作用于内外桶壁上的土压力分布图.从图5(a)、(b)中不难发现,作用于前侧外桶壁和后侧内桶壁上的被动土压力均表现出随埋深先增大再减小的趋势,这与传统的重力式基础形式有着显著的区别,同时也进一步印证了图4(a)、(b)中所反映的转动破坏模式.从图5(c)中可以看出,作用于前侧内桶壁中上部分的主动土压力分布近似等同于静土压力分布,而下半部分的土压力则随埋深的增加而迅速增大,这同样是桶体的转动破坏模式造成的.在图5(d)中,作用于后侧外桶壁上半部分的主动土压力由于土体出现裂缝的原因而近似为0,下半部分的土压力分布特征与图5(c)类似.

3 变动参数比较研究

已有的研究表明[8～10],单桶形基础的水平承载能力主要受到土体材料参数(有效重度γ′和不排水抗剪强度Su)、桶体几何参数(长径比L/D)、荷载作用高度(Lp)等因素的影响.在下文中,通过一系列的变动参数比较研究,分别探讨了上述各因素对于单桶形基础水平承载能力的具体影响效果.

3.1 土体材料参数对水平承载力的影响

3.1.1 土体的有效重度(Su=3.0 kPa,L/D=1.0,Lp=0) 通过变化土体的有效重度γ′,进行5组三维有限元分析,可分别获得与之相对应的单桶形基础水平承载力值.为了便于比较,这里定义Pn=Ph/SuDL(Su=3.0 kPa,L=D=1.0 m)为归一化的水平承载力.于是,将上述所得承载力值进行归一化处理后,结果如图6所示.不难发现,在桶后主动区土体与桶体外表面间发生脱离的接触条件下,单桶形基础的水平承载力随土体有效重度的增加而近似呈线性增长的趋势,但幅度相对较小,对应于 γ′增加28.6%,Pn仅增长4.5%.

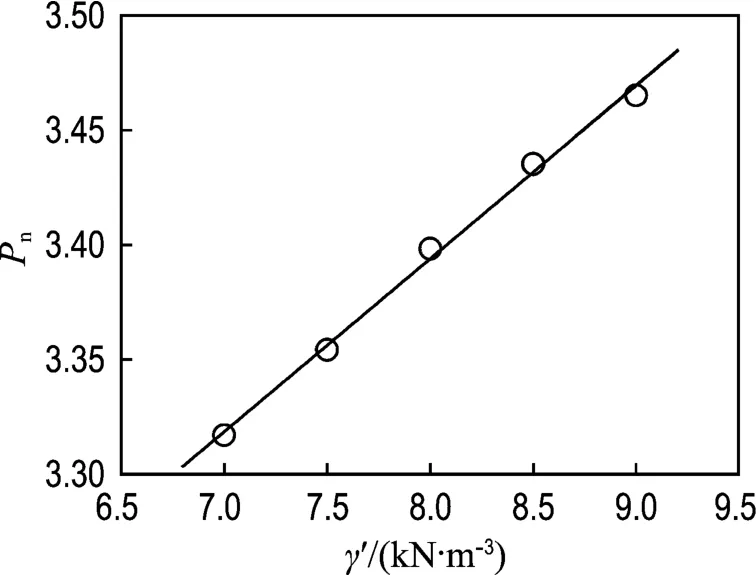
图6 γ′对水平承载力的影响Fig.6 Effect of γ′on horizontal bearing capacity

3.1.2 土体的不排水抗剪强度(γ′=8.0 kN·m-3,L/D=1.0,Lp=0) 参考已有的研究经验可知,土体的不排水抗剪强度是另外一个影响单桶形基础水平承载力的材料参数.为了进一步检验其对承载力的影响效果,本文通过变动土体的不排水抗剪强度值进行了7组数值计算.基于有限元分析结果,可以得到单桶形基础水平承载力随土体不排水抗剪强度的变化关系,归一化后,如图7所示.可以看出,单桶形基础的水平承载力表现出随土体不排水抗剪强度的增加而增长的趋势,且仍近似服从线性分布.

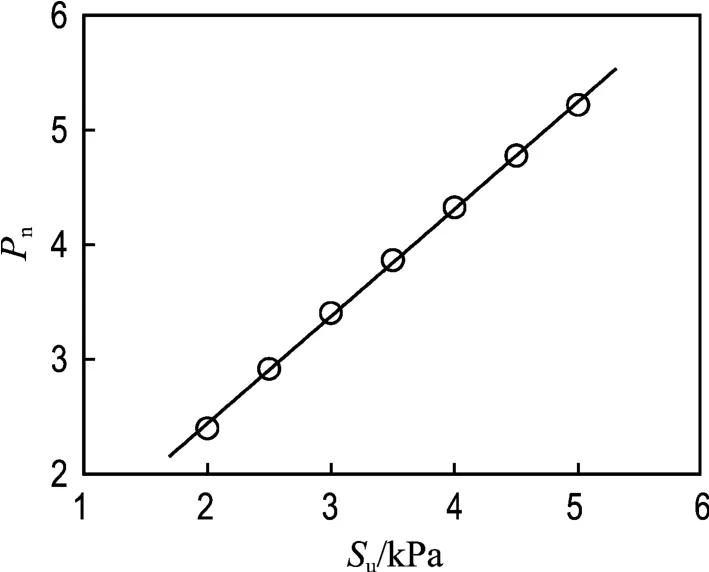
图7 Su对水平承载力的影响Fig.7 Effect of Suon horizontal bearing capacity

3.2 桶体长径比对水平承载力的影响(γ′=8.0kN·m-3,Su=3.0 kPa,Lp=0)

为了得到单桶形基础水平承载力随桶体长径比的变化关系,在以下的数值分析中,令桶体的长径比L/D从0.5均匀变化到3.0,可以分别得到与之相对应的单桶形基础水平承载力值,归一化后,如图8所示.由图可知,单桶形基础的水平承载力随着桶体长径比的增长而增长,近似呈二次曲线分布.这一现象可以从桩基的类似结论中得到较好的理解[11].因为单桶形基础可视为一种特殊类型的短桩,所以其具有与短桩相类似的承载特性也就显得合情合理了.

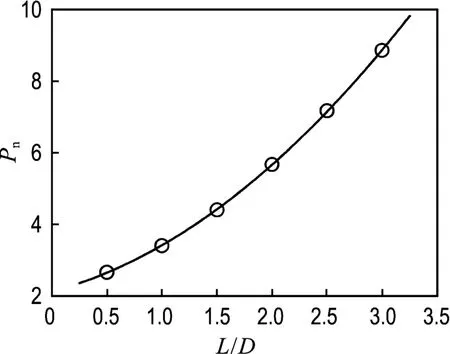
图8 L/D对水平承载力的影响Fig.8 Effect of L/D on horizontal bearing capacity

3.3 荷载作用高度对水平承载力的影响(γ′=8.0 kN·m-3,Su=3.0 kPa,L/D=2.0)

桶形基础作为一种海上结构,随着海平面的涨落,将会受到来自不同高度的水平荷载作用.因此,正确地估算在不同荷载作用高度下的桶形基础水平承载力对于确保基础在使用过程中的安全性和可靠性具有重要的意义.为此,这里选择0～1.0L作为荷载作用高度Lp的变化范围进行数值分析,归一化结果如图9所示.可以看出,单桶形基础的水平承载力随着荷载作用高度的增加而降低,近似呈抛物线分布.这一现象在文献[12]中也得到了论证.于是,在实际的工程设计中应该充分地考虑由于加载高度变化所造成的桶形基础承载力降低问题,以避免意外超载破坏现象的发生.

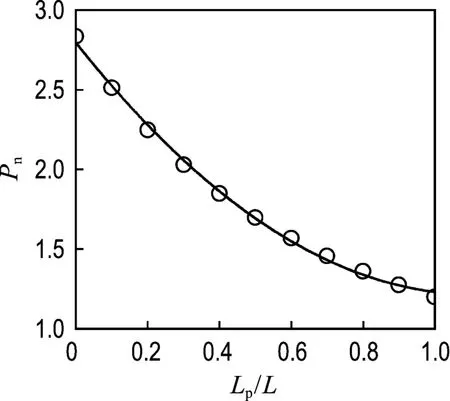
图9 Lp/L对水平承载力的影响Fig.9 Effect of Lp/L on horizontal bearing capacity

4 结 论

(1)通过与室外模型试验结果进行比较,验证了利用三维有限元方法计算单桶形基础水平承载力的可行性.

(2)饱和软黏土地基中单桶形基础的水平破坏模式为转动破坏模式,转动中心位于泥面与基底之间的某点上.

(3)土体的变形模量对桶基达到极限承载状态所需施加的水平位移具有显著影响,而对桶基的水平承载力几乎不产生影响.

(4)由变动参数比较研究可知,单桶形基础的归一化水平承载力受土体有效重度变化的影响较小,随土体不排水抗剪强度、桶体长径比的增大而显著增大,随荷载作用位置的升高而明显降低.

[1]施晓春,徐日庆,俞建霖,等.桶形基础简介及试验研究[J].杭州应用工程技术学院学报,2000,12(增刊):39-42

[2]ANDERSEN K H,MURFF J D,RANDOLPH M F,et al.Suction anchors for deepwater applications[C]//Frontiers in Offshore Geotechnics.Netherlands:Taylor and Francis Group,2005

[3]张 伟,周锡礽,余建星.滩海桶形基础极限水平承载力研究[J].中国海洋平台,2004,19(3):14-16

[4]施晓春,徐日庆,龚晓南,等.桶形基础单桶水平承载力的试验研究[J].岩土工程学报,1999,21(6):723-726

[5]CHEN W.Limit Analysis and Soil Plasticity[M].New York:Elsevier Scientific Publishing Company,1975

[6]SUPACHAWAROTE C, RANDOLPH M,GOURVENEC S.Inclined pull-outcapacity of suction caissons [C]// Proceedings of 14th International Offshore and Polar Engineering Conference.Toulon:International Society of Offshore&Polar Engineering,2004

[7]HIBBIT K,SORRENSON P R I M.ABAQUS User′s Manual(Version 6.3)[M].Rhode Island:Pawtucket R I,2002

[8]ZDRAVKOVIC L,POTTS D M.Parametric finiteelement analyses of suction anchors[C]//Frontiers in Offshore Geotechnics.Perth:Taylor&Francis,2005:297-302

[9]MCCARRON W O,SUKUMARAN B.Ultimate capacities of suction caissons and pile elements for deepwater applications[C]//Proceedingof the Tenth International Offshore and Polar Engineering Conference.Seattle:International Society of Offshore&Polar Engineering,2000:466-469

[10]RANDOLPH M F.Effect of strength anisotropy on capacity of foundations[C]// Proceedings of the John Booker MemorialSymposium.Sydney:Balkema,2000:313-327

[11]BROMS B B.Lateralresistance of piles in cohesiveless soils[J].Journal of the Soil Mechanics and Foundations Division,1964,90(SM2):27-63

[12]范庆来.软土地基上深埋式大圆筒结构稳定性研究[D].大连:大连理工大学,2006