窄带小群时延波动晶体滤波器设计*

(成都天奥电子有限公司,成都 611731)

1 引 言

随着无线电技术的迅速发展和无线电设备应用领域的扩大，整机对晶体滤波器(以下简称滤波器)时域特性的要求也越来越高。特别是在数据传输系统中，起中频滤波作用的窄带晶体滤波器时域特性的好坏，已经成为整个系统中影响数据传输的原因之一。因为信号通过晶体滤波器后，会引起相位突变，那么信号高速传输时，在解调过程中，会造成误码率高，影响整机的数据灵敏度和残余误码率。则整机在系统联试时，由于滤波器存在的群时延波动特性，当这一波动过大时，就会造成系统终端数字信号出现误码和乱码现象，严重影响整机系统的性能，最终造成系统性能变差。因此，为了尽可能使有用信号通过滤波器而不失真，就要求滤波器不仅有很好的幅频特性，而且还要有线性的相频特性，即信号通过滤波器后其延迟时间最好为一常数。

本文采用最经典的差接桥型晶体滤波器电路，为了保持在带宽的一部分中有恒定群延迟，而且还要保持较高的选择性，滤波函数选择频域特性中衰减最好的切比雪夫函数和时域中群时延特性最好的贝塞尔函数进行对比分析介绍，研究出一种特殊传递函数，称为半线形滤波器[1]，在带外具有切比雪夫函数的衰减特性，带内则具有贝塞尔函数的平坦群时延特性。

2 滤波器的相移和群延迟分析

我们知道，滤波器的带宽直接影响相移特性斜率的大小，一般说来，通带越宽，滤波器的线性相移频率特性就越容易实现，且斜率亦越小，而晶体滤波器多属窄带范畴，因此，实现其线性相移频率特性的难度就较大。此外，阻带衰减的快慢也影响着相移频率特性，即滤波器的传输节点的多少和分布位置决定其通带的光滑程度。节点数目越多，相移的绝对值越大，滤波器的延迟时间增加，致使整个电路反应迟钝。例如，在差接桥型滤波器中，每增加一块晶体，将会带来约100°左右的相移[2]。但是增加传输节点的数目对衰耗特性有好处，使滤波器衰减变得更陡峭。

从以上分析可知，滤波器的幅频特性和相频特性是一对不可完全调和的矛盾，只能从设计上来平衡。本文介绍的这种窄带小群时延波动晶体滤波器设计，就是在确保窄带滤波器在频域特性方面较好的选择性优势情况下，融入了线性相移设计技术，大大提高了窄带晶体滤波器的相位的线性度，使晶体滤波器不但具有带宽窄、阻带衰减高等频域特性，而且在全通带范围内还具有群时延波动小和相位一致性好等时域特点，突破了传统意义上单纯的频域晶体滤波器或时域晶体滤波器的界线，充分体现了滤波器频域特性和时域特性这一对矛盾的对立统一。下面以应用于工程中的晶体滤波器设计为例介绍这种滤波器的设计过程。

3 两种滤波函数设计对比及折衷

3.1 晶体滤波器的技术指标

晶体滤波器的主要技术指标如下：

3 dB带宽>±35 kHz,40 dB带宽<133 kHz,插入损耗<3 dB,50 kHz群时延波动<1 μs，70 kHz群时延波动<2 μs,最终衰减>80 dB,工作温度-40℃～+70℃。

从以上技术要求可知，该晶体滤波器的特点是：带宽窄(相对带宽为0.056%)，群时延波动小，阻带衰减高，矩形系数较小(BW40/BW3<3.7)。

3.2 滤波器电路原理和主要元件计算

根据技术指标要求，采用四晶体两节差接桥型电路即可实现以上的幅频特性指标。滤波器电路原理图如图1所示。

图1 滤波器电路原理图

图1中主要元件的计算公式如下[3]：

(1)

(2)

(3)

(4)

式中，f0为滤波器的中心频率，B3为滤波器的3 dB带宽，K12、K23、K34为归一化低通耦合系数，f1～f4为晶体的串联谐振频率。

电路中变量器LT的设计公式由式(5)来计算，一般在允许情况下，LT的值尽量大一些。

(5)

RT选RTS、RTL中较大的一个，Qt为变量器品质因数，RTS、RTL分别为滤波器输入和输出端的特性阻抗，按以下公式计算：

(6)

(7)

(8)

式中，q1、qn为归一化质量因数，LS为石英晶体的等效动态电感。

滤波器进行阻抗变换后的匹配线圈L1、L2按公式(9)和(10)进行：

(9)

(10)

式中，n11、n12为变量器的匹配圈数，n2为变量器的双绕圈数，若RTS=RTL，则n11=n12。

而电路中的电容值在实际工程中采用微调电容，以便于获得更好的滤波特性，故在此不列出计算公式。

3.3 两种滤波函数的设计及仿真比较

我们对切比雪夫和贝塞尔函数各选择了一组q、K值，见表1。

表1 两种滤波函数的归一化低通耦合系数与归一化质量因数

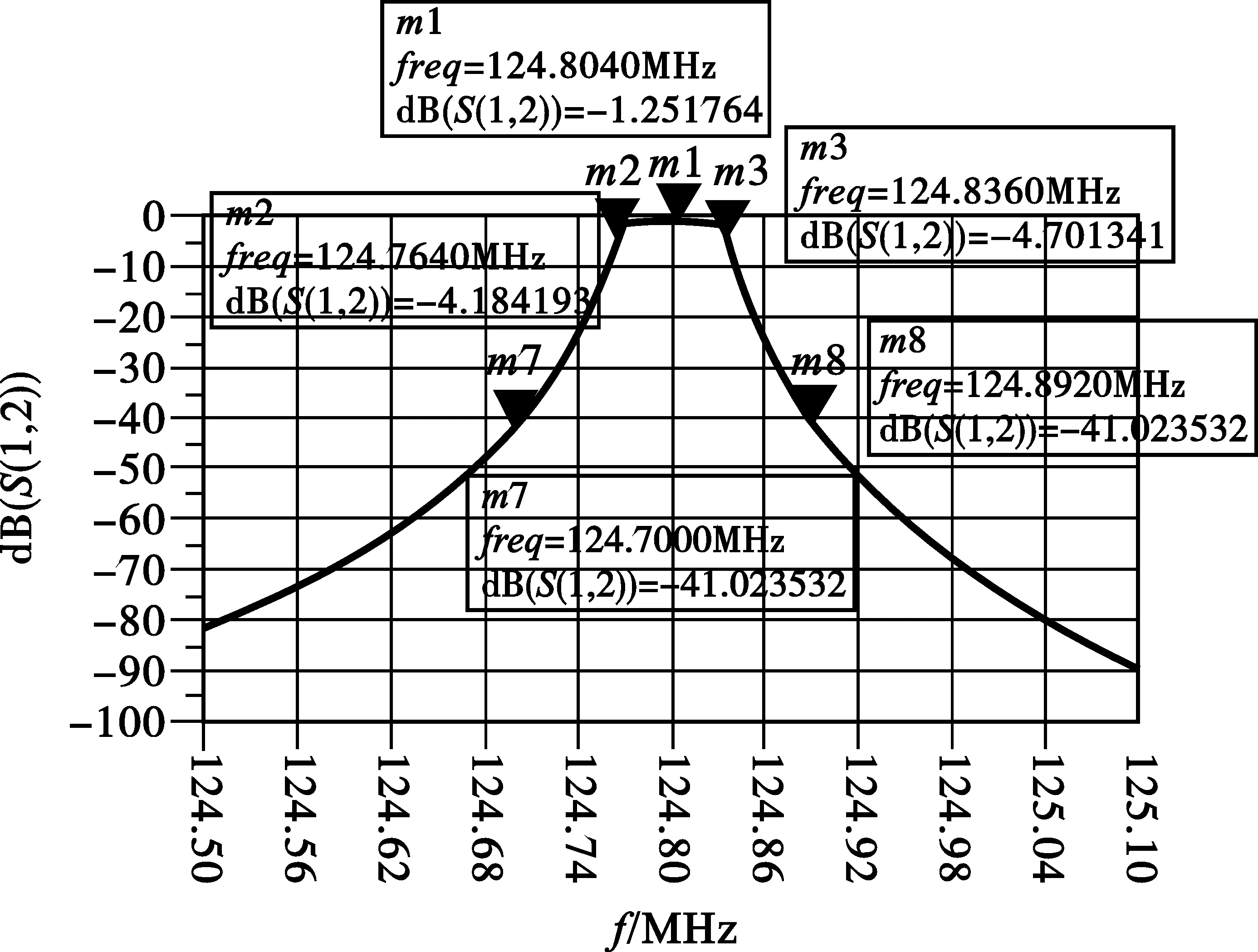
(a)幅频特性

(b)50 kHz 带宽群时延特性

在设计中，滤波晶体采用的圆片，其动态电感均值为1.7 mH，根据公式(1)～(10)，我们计算出这两种滤波器的各元件值，并通过仿真来比较两者的优缺点，如图2和图3所示。

从图2和图3两个仿真设计中我们可以得出这两种函数滤波器在相同电路形式情况下所达到技术指标与要求值之间的差距，如表2所示。

(a)贝塞尔幅频特性

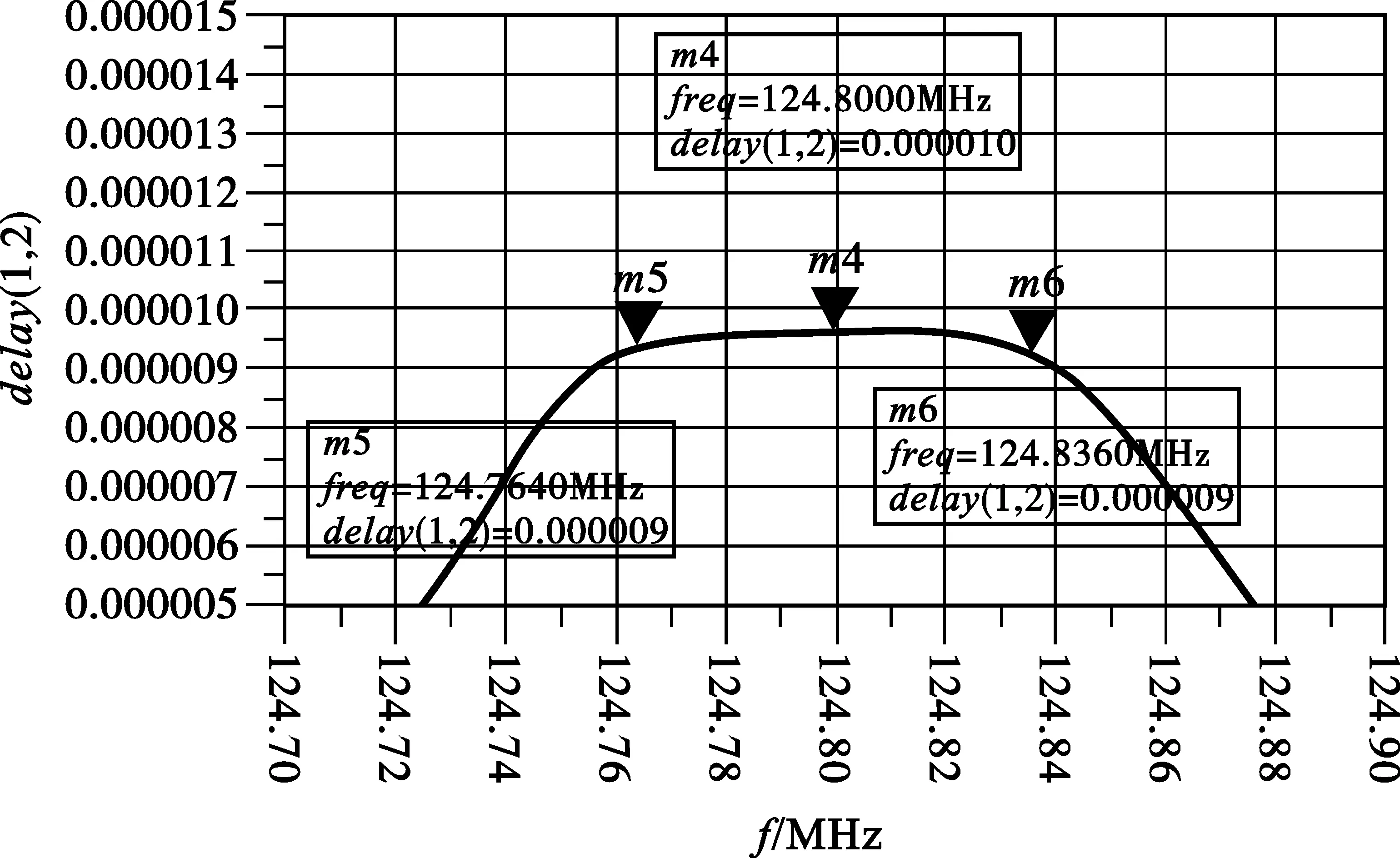
(b)70 kHz 带宽群时延特性

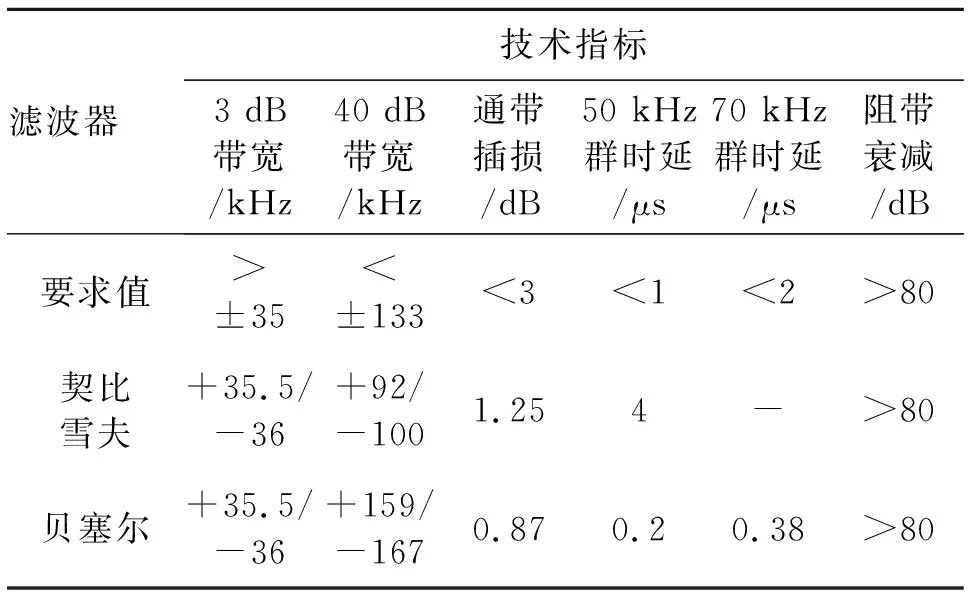
滤波器技术指标3 dB带宽/kHz40 dB带宽/kHz通带插损/dB50 kHz群时延/μs70 kHz群时延/μs阻带衰减/dB要求值>±35<±133<3<1<2>80契比雪夫+35.5/-36+92/-1001.254->80贝塞尔+35.5/-36+159/-1670.870.20.38>80

3.4 滤波器折衷设计

从表2可知，契比雪夫滤波器在幅频特性方面优于要求值，而贝塞尔滤波器在相频特性方面优于要求值，若能在两者之间取长补短，寻求一个平衡折衷的方法，那么就可完全满足技术指标要求。通过分析，我们了解到这两种滤波器在电路上不同之处在于晶体频率值的不同，那么调整晶体频率值是否可以满足技术指标要求呢？我们重新通过仿真来验证这种推测。仿真结果如图4所示。

(a)幅频特性

表3给出了改进后的滤波器电路仿真测试值与改进前的两种滤波器和要求值之间的比较。由表可知，改进后的滤波器的40 dB带宽在契比雪夫和贝塞尔滤波器之间，但较靠近契比雪夫的幅频特性，而50 kHz带宽范围的群时延波动与贝塞尔一样，只是70 kHz带宽范围的群时延波动增大了1 μs，但是仍然比要求值小，而且还有较大的富裕量。由此知改进后滤波器的通带保持了时域函数贝塞尔的平滑群时延波动特性，而过渡带和阻带则保持了频域函数契比雪夫的小矩形系数高衰减的幅频特性，说明这种融合了契比雪夫和贝塞尔函数特点的小群时延波动滤波器的设计是可行的。

表3 改进后仿真值与要求值比较表

4 实际产品的测试结果及分析

根据前面的设计和分析，我们通过实际电路进一步验证其在现实中的可行性。表4为实测滤波器的技术指标与仿真和要求值的比较表，图5为实际产品的测试曲线图。由表4可知，这种方案的通带特性非常逼近仿真曲线结果，阻带特性的寄生目前还不能通过计算机仿真出结果，但是阻带宽度和衰减特性则靠近仿真结果，群时延特性也逼近仿真值，50 kHz群时延波动差0.1 μs左右，70 kHz群时延波动差0.1 μs左右，这些差值都是在误差范围内，故结果是满足所有指标要求的。

表4 滤波器实测值与仿真值和要求值比较表

(a)实测产品的幅频特性

(b)实测产品的群时延特性

该项设计技术在2009年新品设计定型会议上被专家评定为“达到国际先进水平”。应用该技术研发的实用化产品已经提供给多家用户使用，是目前国内唯一一家被认可的生产单位，现已进入小批量生产阶段。与国外相同产品比较，该产品的插入损耗要小2 dB左右，阻带衰减要高5 dB以上，唯一不足之处是在宽温度范围内，70 kHz带宽范围内群时延波动的稳定性比国外产品要差0.3 μs左右，这是产品中所采用的磁环稳定性不一样造成的。

5 结束语

当前，整机的小型化、数字化、抗干扰性能等要求在不断提高，对于晶体滤波器的要求也同等在增加，单纯的频域特性滤波器和时域特性滤波器已不能满足整机发展的需求，因此这种介于两者之间的滤波器设计方法今后将会越来越多地应用到实际产品中去。仿真技术的发展和应用为这种设计方法和缩短研制周期提供了可能。

在本文中，我们提出了获得较好群时延波动的改进型设计思路的可行性，并通过实际的电路实现了这种滤波器，该滤波器在实际应用中获得了用户认可。除了这种设计方法外，也可采用六晶体电路的贝塞尔滤波函数来实现，但是这样除了增加成本外，由于高基频晶体老化较大，多采用两个晶体也就增加了滤波器失效的几率，会降低滤波器的质量可靠性。

参考文献：

[1] 方秀峰.线形相位滤波器[J].压电晶体及其应用，1993(3)：121-128.

FANG Xiu-feng.Linear phase filter[J].voltage compensation crystal and its application,1993(3):121-128.(in Chinese)

[2] 周立人.线性相移晶体滤波器的计算机辅助分析[J].压电晶体技术，1987，9(3)：28.

ZHOU Li-ren.Linear phase-shift Crystal filter computer aid analysis[J].voltage compensation technology,1987,9(3):28.(in Chinese)

[3] 李忠诚.现代晶体滤波器设计[M].北京：国防工业出版社，1981：40-47.

LI Zhong-cheng.Modern crystal filter design[M].Beijing:National Defence Industry Publishing House,1981:40-47.(in Chinese)