强干扰下群时延失真对伪码测距性能的影响研究

刘 涛，蒙艳松，张立新

（西安空间无线电技术研究所 陕西 西安710071）

随着导航技术的迅速发展和在各个领域日益广泛的应用，对时间同步要求也越来越高。而时间同步系统中的射频电路、混频器等设备产生的群时延影响着信号的传播时延，而这也进而影响伪码测距以及时间同步精度。Nandi A.K及耿虎军等在文献[1]提出：当系统带内群时延变化幅度小于1/4个码片宽度时，群时延对测距的随机误差影响很小，带内群时延曲线形状的改变会影响距离测量的数据，但该影响可以通过系统的热稳定性设计使之达到一个较小的值。朱祥维[2]等对此模型稍加改进，在仿真实验的基础上，指出2阶群时延对伪距的测量有较大影响。但是目前的研究中都没有考虑到导航信号中存在干扰的情况，针对这个问题，首先从群时延的新定义出发，从理论和仿真两方面出发，首先给出了存在干扰条件下，群时延对伪码测距的理论推导，然后分别对存在干扰条件下线性群时延和抛物线群时延对伪码测距的影响进行仿真。通过理论分析和仿真结果结合，分析强干扰条件下群时延和伪码测距的关系。

1 群时延的新定义

群时延是线性系统中重要的传输特性参数,其定义为群信号通过线性系统或网络时,系统或网络对信号整体产生的时延。它包括绝对群时延和相对群时延，群时延失真主要是由是相对群时延，后者与信号传输失真有密切关系,其定义为相位对角频率的微商：

这里Φ(ω)是系统传输函数的相位响应。

群时延反映的物理含义是被测网络的相位线性度,为了描述系统的相位畸变,可以将相位特性用Taylor级数展开,得到线性项和其他项.朱祥维在文献[2]中提到了基于Taylor级数展开的新群时延定义推导出零阶群时延、一阶(线性)群时延和二阶(抛物线)群时延。假设系统相位响应在ωc处连续高阶可导，根据Taylor公式，得到其展开：

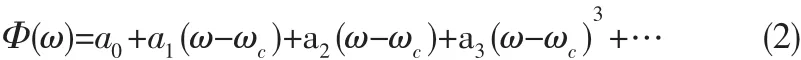
而根据公式(1)，我们得到了a0为绝对群时延，a0为线性群时延，a0为二阶群时延。

2 强干扰下群时延对伪码测距误差的推导

导航系统信号发射的原理框图如下，对导航信号进行伪码调制和载波调制，由于传播信道中引入的干扰，信号成分变得复杂，在接收端经过滤波之后的信号做载波相关和伪码相关，这里，我们假定对信号的载波实现完美跟踪。而群时延我们采用滤波器来等效。

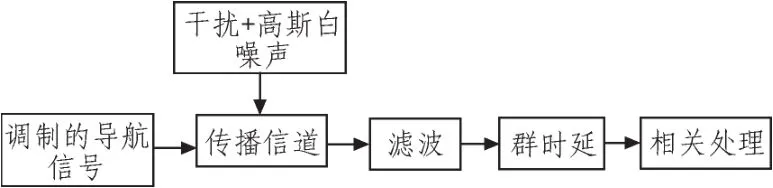
图1 信号群时延失真等效模型Fig.1 Equivalent signal model of group delay distortion

将接收到的信号记为：

其中s(t)是导航信号，i(t)是干扰信号，n(t)是高斯白噪声信号，经过滤波器群时延之后的信号为：

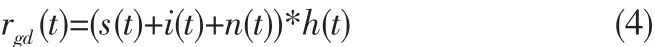
这里h(t)的是系统群时延的时域形式。

按照前面所述，假设载波完美跟踪和剥离的情况下，在接收端对接收到的信号做码环相关处理：

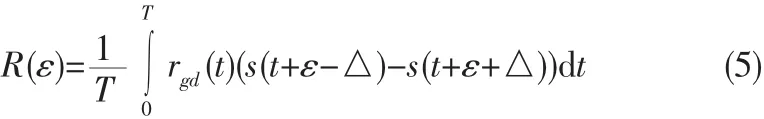
这里ε是时延误差，△是码环相关间隔，早码与即时码码相位差。

根据Betz在文献[3-4]中的推导以及文献[5]提出的码环线性理论，在时延误差ε很小的情况下，码环鉴别器输出呈现出线性特性，当不存在群时延和干扰的情况下，Betz得到码环鉴别器对时延误差的导数，即鉴别器增益K，以及测距误差

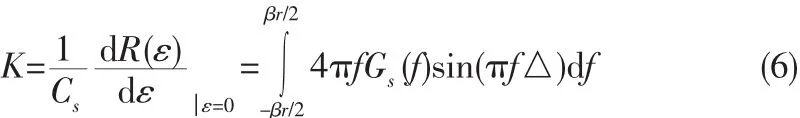
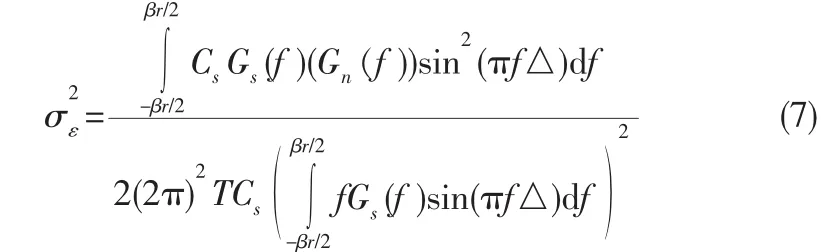
其中 Gs（f)是导航信号归一化功率谱密度，Gn（f)为噪声功率谱密度，βr是接收前端带宽由于理论推导较为繁琐所占篇幅较大，所以不作详细推导，详细推导见文献[3-4]，根据公式和公式，得到了存在群时延和干扰条件下的码环测距误差的理论推导公式为：

通过理论推导可以发现，群时延改变了码环鉴别增益，但在群时延失真信道在幅频响应恒定的时候，其测距误差影响不大。而干扰的出现相当于降低了SNIR[5]，两者共同存在的情况下，信号的SNIR降低和码环增益的改变恶化测距误差。

3 仿真分析

基于群时延是相位响应与频率之间的对应关系，本次仿真采用的干扰的是宽带线性扫频式干扰，其表达式为：

这里f0和f1是常量，θ是初始相位。a(t)是干扰包络，本次仿真取包络为恒值。

本次仿真采样频率为10 MHz，伪码速率为1.023 MHz，干信比为30 dB，积分时间为0.1 s，并取500次蒙特卡洛仿真结果分别得到三组测距值的均值和基本差。本次仿真主要研究的是线性群时延和抛物线群时延，采用三组不同时延范围进行对比，即在同一时延范围内线性群时延和抛物线群时延的横向对比以及不同取值范围内测距误差的纵向对比。

图2 线性群时延和抛物线群时延Fig.2 Linear and parabolic group delay

线性群时延取三组：0～8 ns，0～15 ns 以及 0～20 ns 三个范围，如图所示为0～8 ns线性群时延信道的仿真结果。

通过鉴相曲线可以看到，强干扰的出现使得鉴相曲线在零点附近的测量值发生了畸变，根据400次蒙特卡洛仿真结果测得的数据，未经过群时延失真信道的鉴相曲线时，干扰的引入使得过零点偏移大概为-0.42 ns，而经过群时延失真之后，过零点偏移大概为-0.57 ns，两者偏差为0.15 ns，说明群时延的加入使得干扰信号对测距时延的影响变得更大，对此的解释是，线性扫频式干扰对于群时延失真信道反应较为剧烈，进一步干扰了信号的传输时延的准确测量。鉴于仿真结果图形过多，不一一列举，表1给出了测得的实际结果。

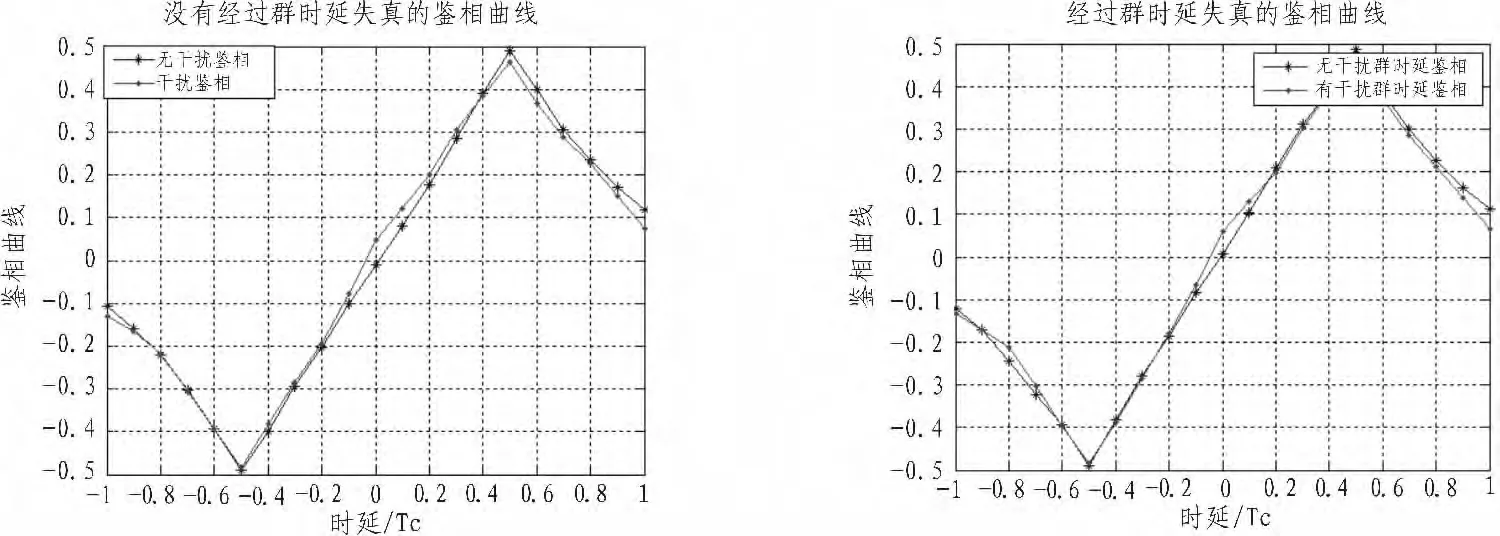
图3 未经过和经过群时延失真信道的鉴相曲线Fig.3 The pseudo-code phase curve with and without group delay distortion

图4 无干扰时伪码鉴相曲线和有干扰时的伪码鉴相曲线Fig.4 The pseudo-code phase curve without and with interference

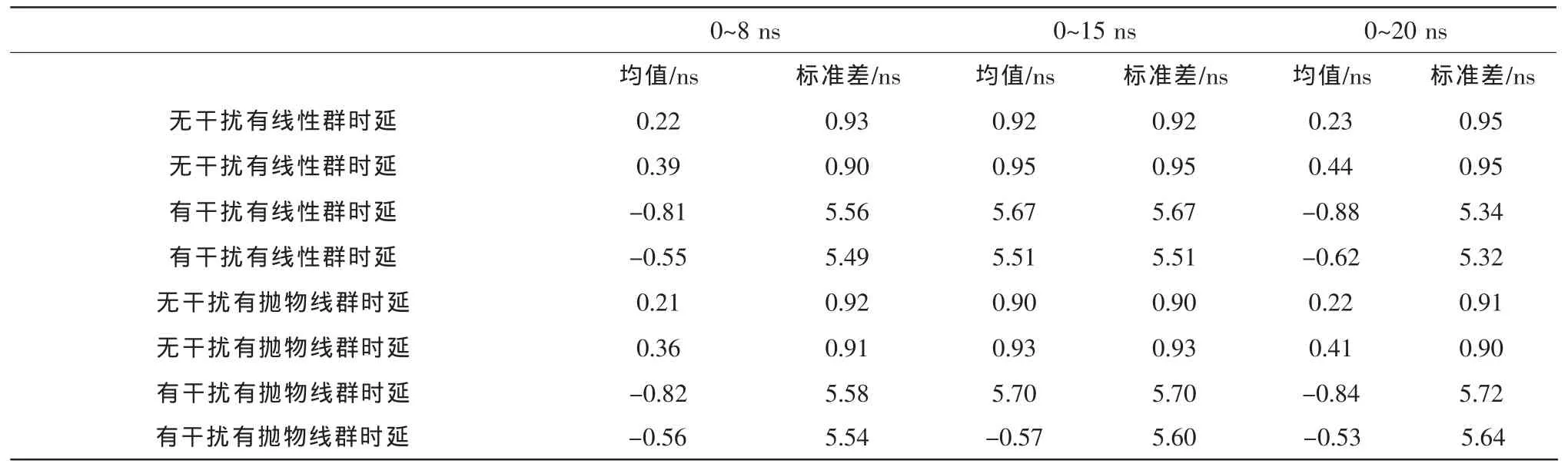
表1 伪码测距均值和标准差Tab.1 Pseudo-code ranging mean and standard deviation

通过结果我们得到：

1)群时延失真对测距标准差影响不大，对过零点偏移有一定影响。

2)扫频式强干扰的引入恶化了伪码测距性能，特别是对测距标准差的影响更大。

3)群时延变化范围越大，过零点偏移越大，但并不是很明显。

4)相同变化范围内的线性群时延和抛物线群时延对测距影响相差不太大。

4 结论

通过理论分析和仿真验证，理论分析表明，群时延信道改变了鉴别增益而影响测距误差，但在群时延信道的幅频特性保持恒定的时候，影响并不明显。仿真结果表明，强干扰的加入加大了群时延失真对鉴相曲线过零点的偏移；群时延失真范围越大，即相位响应随频率变化越敏感，过零点偏移会越大；相同群时延失真范围内，线性群时延和抛物线群时延对测距的影响差别不大。

[1]耿虎军.系统群时延特性对伪码测距影响的研究[J].无线电工程,2004,34，(11):27-29.GEN Hu-jun.Study on the effect of system group delay on PN ranging[J].Radio Engineering,2004,34(11):27-29.

[2]朱祥维,孙广富.相位非线性畸变对伪距测量的影响［J］.国防科技大学学报，2008(6):101-106.ZHU Xiang-wei,SUN Guang-fu.The Impact of Phase Nonlinear Distortion to GPS Pseudo-range Measurement[J].Journal of the National Defense University,2008(6):101-106.

[3]Betz J W,Kolodziejsk K R.Generalized theory of code tracking with an early-late discriminator.Part I:Lower bound and coherent processing[J].IEEE Transactions on Aerospace and Electronic Systems,2009，45(4):1538-1550.

[4]Betz J W,Kolodziejsk K R.Generalized theory of code tracking with an early-late discriminator. Part II:Noncoherent Processing and Numerical Results[J].IEEE Transactions on Aerospace and Electronic Systems,2009，45(4):1551-1564.

[5]Parkinson B,Spilker J,Axelard P,et al.Van Dierendonck GPS receivers in Global Positioning System:Theroy and Applications[C]//AIAA,1996:329-408.

[6]Balaei A T.Statistical Inference Technique in Pre-Correlation Interference Detection in GPSReceivers[M].ION GNSS,Fort Worth,TX,2006.