一种基于Chebyshev函数的新型带通滤波器设计方法*
(中国西南电子技术研究所,成都 610036)
1 引 言
近几年来,随着宽带通信技术的迅速发展,其系统对滤波器性能的要求越来越苛刻,特别是在某些军用机载设备中,为了发射机宽带工作,同时保证发射机谐波抑制、整机效率、边带响应等多项战术指标,其整机对输出滤波器的插损、谐波抑制、体积和通过功率等都提出了高性能要求。目前,国内高性能滤波器设计多采用传统切比雪夫(Chebyshev)函数、椭圆函数或改进型的椭圆函数等设计方法[1]。传统切比雪夫器件由于插损大、级数多且生产出来的滤波器体积大、成本高,不能满足现代通信的需求;椭圆函数带通滤波器虽然有较好的选择性,但由于对元器件精度要求极高、实现复杂、调试困难,且其传输零点都是成对地出现在通带的两侧,设计缺乏灵活性,难以推广应用,从而使得高性能的滤波器设计成为一个难点。
针对这些问题,本文研究了一种新型的拓扑电路来实现带通滤波器设计,可称为“准椭圆函数”滤波器[2],既克服了传统函数滤波器的缺点,又具有很好的设计灵活性。
2 新型拓扑电路的组成框图及设计过程
新型滤波拓扑电路的基本设计思路:首先选择一个阶数较少的切比雪夫函数带通滤波网络作为基本电路;针对基本电路模型阻带衰减下降缓慢的问题,在其通带边缘灵活地引入有限传输零点,改善其阻带抑制性能;合理运用等效网络变换等手段得到更易于实现的电路结构,从而实现最终的新型拓扑电路设计。其简单的组成框图如图1所示。
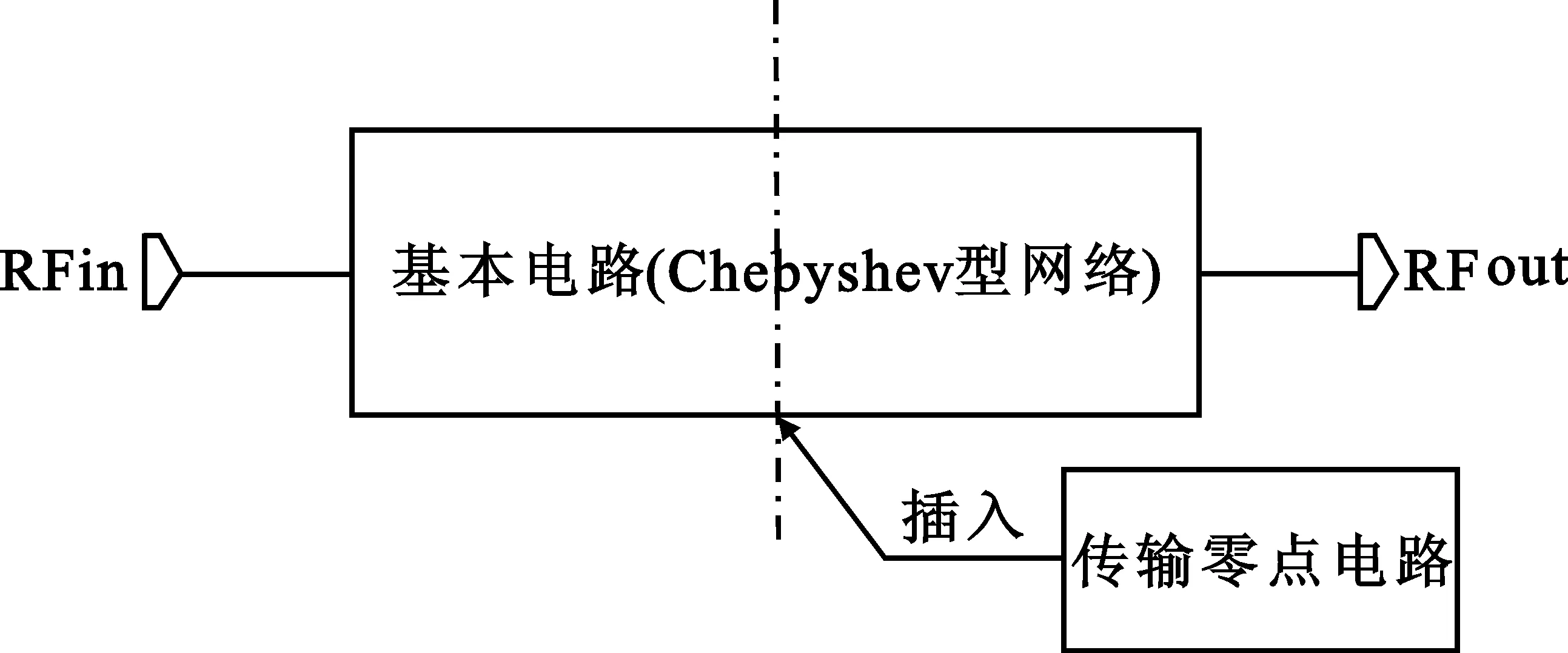
图1 新型拓扑电路组成框图
2.1 基本电路的设计
传统的滤波器设计,通常采用综合法设计理论。其中带通滤波器拓扑电路均以低通原型参数为基础通过频率变换的方法实现。低通滤波器转换为带通滤波器的原则[3],这里简述如下:
(1)将低通电路的每个电容并联一个电感,使它们并联谐振于中心频率;
(2)将低通电路的每个电感串联一个电容,使它们串联谐振于中心频率。
传统的Chebyshev型带通滤波器基本电路的设计,在很多的相关书籍中都有详细介绍,这里就不再重复叙述,其基本方法简单介绍如下:根据选定的滤波器的阶数n和最大通带纹波Ar,查表得到相应的低通滤波器原型;再根据低通滤波器与带通滤波器的转换原则,即可设计出Chebyshev型带通滤波器基本电路[4]。图2是三阶Chebyshev型带通基本电路。
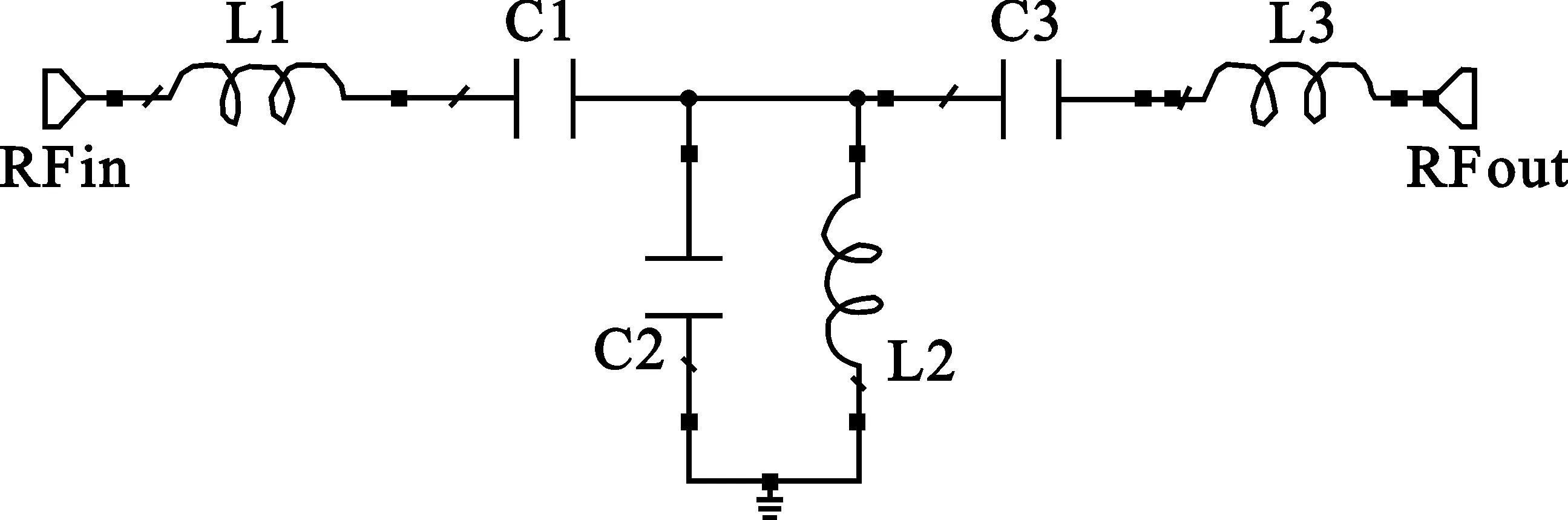
图2 三阶带通电路
2.2 传输零点的放置,改善阻带抑制
由于低阶数的传统Chebyshev带通滤波器阻带抑制特性较差,很难满足现代通信的高性能要求。在该新型的拓扑电路设计中,在保证原有通带特性不变的情况下,通过在其通带边缘放置有限传输零点来改善其阻带抑制特性,这样可以在不增加滤波器阶数的情况下实现高的阻带抑制性能,同时可以得到较低的插入损耗。
传输零点电路的设计思路:首先保证传输零点电路与基本电路在通带范围内阻抗匹配,确保滤波器通带特性保持原有特性;再根据滤波器阻带抑制的实际需要来确定插入传输零点的个数及其频率大小(根据经验积累,通带边缘每插入一个传输零点,可使相应的带边衰减增加约20 dB)。图3为单个传输零点电路图,电路中各元件值由通带带宽频率、传输零点频率及阻抗决定。
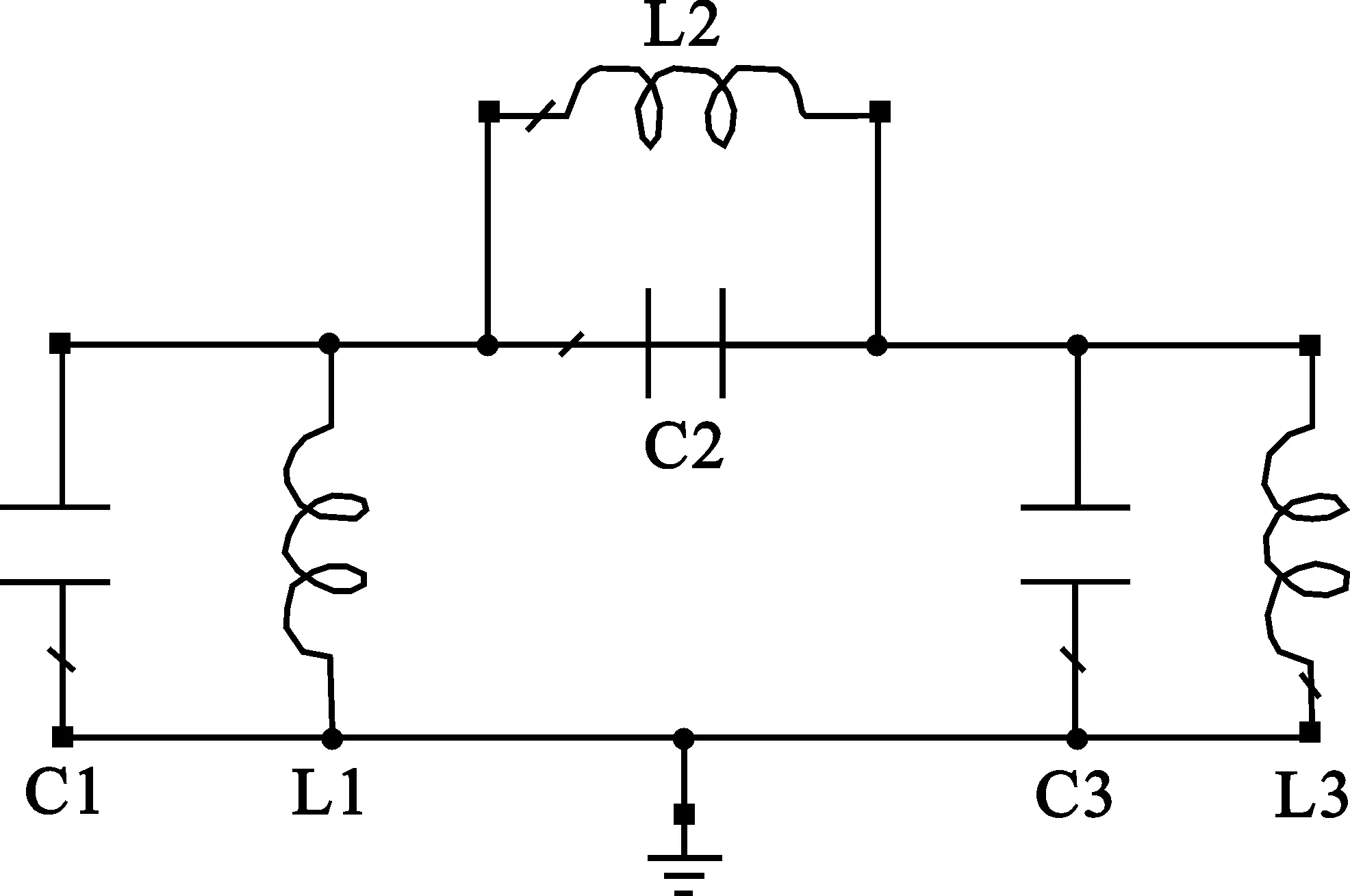
图3 传输零点电路
电路中各元件值计算公式如下:
(1)当fzero>fH时,即传输零点在通带的右侧边缘。
(1)
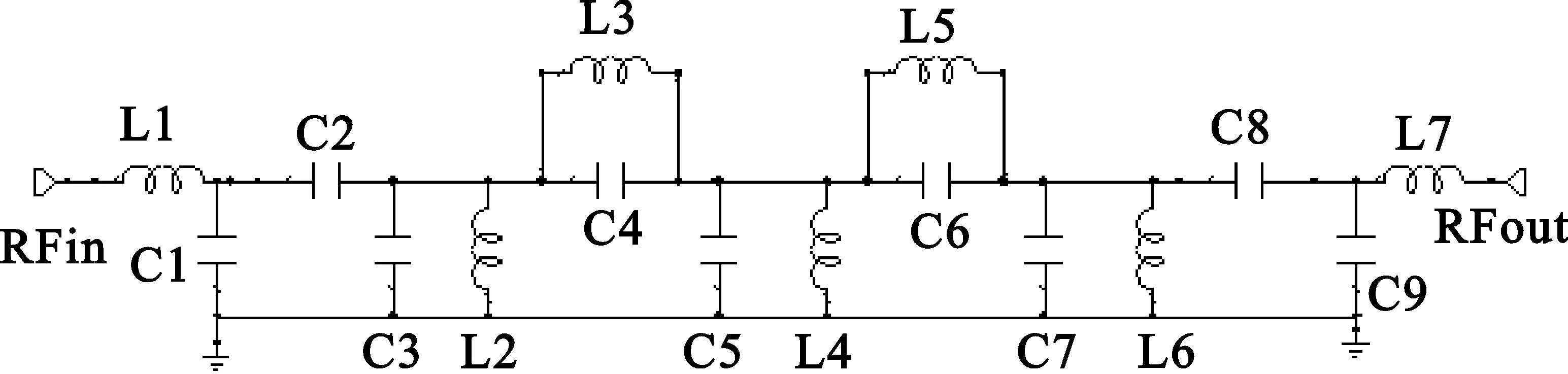
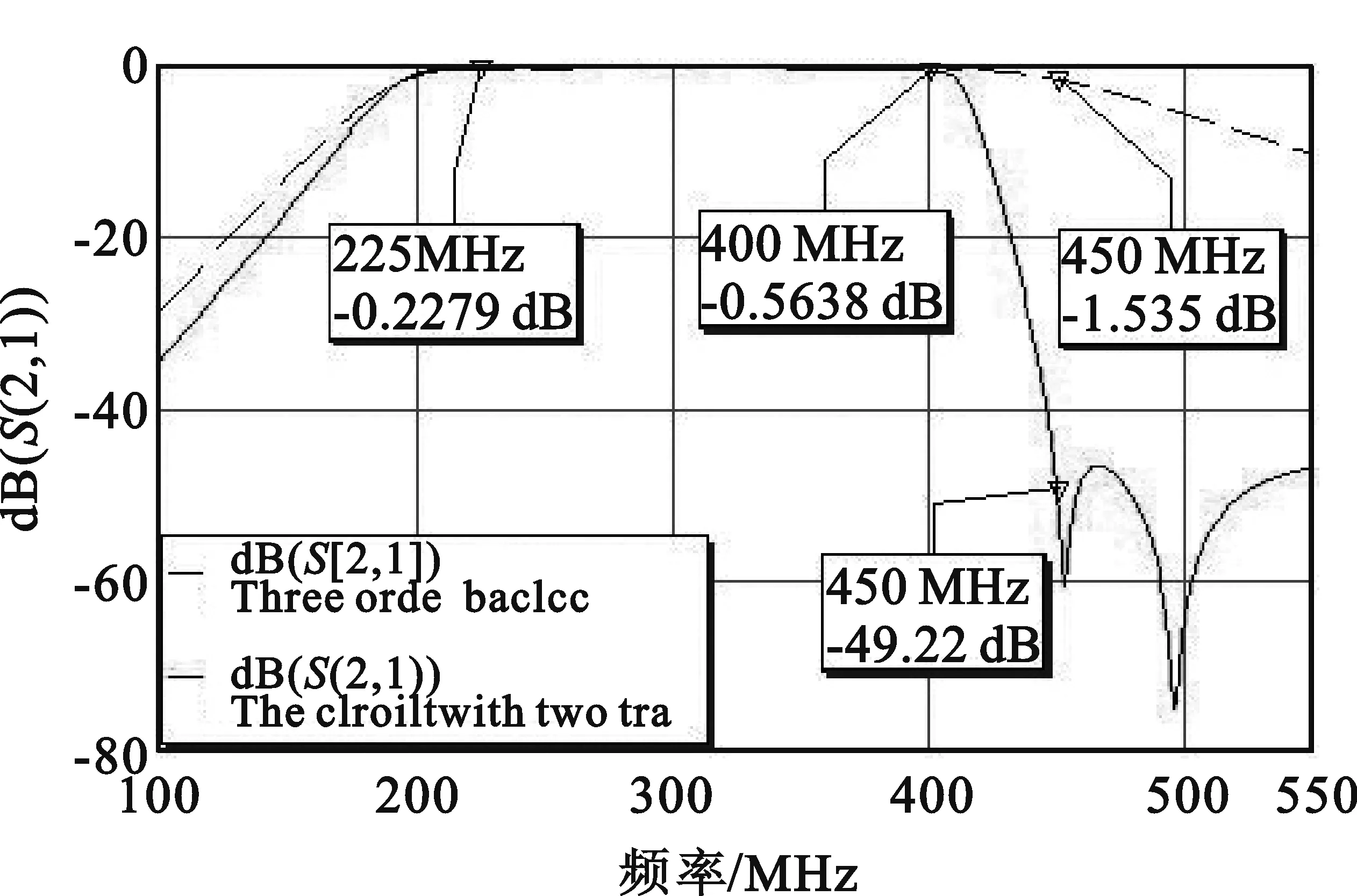
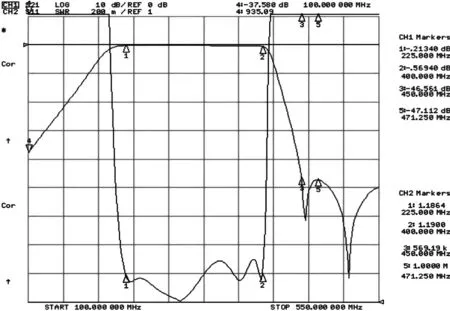
(2)当fzero (2) 其中: (3) 式中,R为特性阻抗,fL为通带低端截止频率,fH为通带高端截止频率,fzero为传输零点频率。 设计好基本电路和传输零点电路后,根据巴特莱特二等分定理将基本电路从正中央加以分割(可保证原有阻抗不变)[3],并将设计好的传输零点电路插入到分割位置处,即可得到新型拓扑结构的滤波电路。图4是在三阶基本带通电路的基础上插入2个传输零点后的拓扑电路。 图4 带两个传输零点的带通电路 图4在电路形式上仍有很多的缺陷,如存在悬空节点(L1与C1间)、元件值离散性较大、部分元件值较难实现等,这些固有的缺陷会给电路制作带来一系列的困难,如增加电路的不稳定性,因为分布参数的存在而严重影响滤波器的性能,使得实际制作的滤波器与设计值相差太大等,特别是在高频应用时,这些问题将会显得更加严重,甚至电路都无法实现。 诺顿变换是解决上述缺陷问题的有效办法之一。诺顿变换的基本单元变换关系[3]在很多专业书籍中都有介绍,这里不再赘述。 通过对图4电路中C1、C7处分别插入理想变压器T1、T2, 合理选择变量器的变比n,经诺顿变换后,即可得到最终的新型滤波电路,如图5所示。值得注意的是,当变量器T1、T2的变比n取相同值时,新型滤波电路的输入、输出阻抗值将保持原有的阻抗特性不变。 图5 带两个传输零点的最终电路 由图5可知,电路中已不存在悬空节点的问题,任何一个连接节点处都有设计电容接地。根据变压器特性,如选择一个合理的变比值n,则变压器T1、T2 间的元件值将相应地放大(或缩小)n2倍,这既减小了元件值间的离散性,又很好地解决了部分元件值较难实现的缺点。故此新型带通滤波电路很好地解决了传统Chebyshev型带通滤波电路中一些固有的缺陷问题,又因有传输零点的引入,从而大大改善了滤波器阻带衰减的陡峭度;且相对椭圆函数滤波电路而言,此新型滤波电路对元器件精度要求较低,电路更为简单,调试容易,设计时可以根据实际需要任意放置传输零点,非常适合灵活设计与应用。 通带频率为225~400 MHz,通带插损小于等于0.7 dB,驻波比小于等于1.4,阻带抑制大于等于45 dB(450 MHz外),输出功率为120 W,工作温度为-55℃~+85℃,输入输出阻抗为50 Ω。 分析上述技术指标可知,滤波器通带插损要求很小,通带高端的衰减相当陡峭而另一侧却无特殊要求。该类型的滤波器用传统函数滤波器实现时,体积大,成本也高,且难以达到最佳效果。运用本文中的新型拓扑电路设计,灵活放置传输零点的位置,可以产生非对称的频率响应,相当于把滤波器的阻带抑制能力都集中在所需的一侧,从而可以减小滤波器的节数和插入损耗,降低设计成本及体积,是设计该类型滤波器的理想方式[5]。 本方案中选用了三阶Chebyshev型带通基本电路,在阻带高端插入两个传输零点的方法来实现电路的设计,电路图如图5所示。电路元件参数为L1=36.64 nH,C1=2.82 pF,C2=5.1 pF,C3=4.82 pF,L2=55.82 nH,C4=5.56 pF,L3=22.09 nH,C5=6.66 pF,L4=90.53 nH,C6=3.16 pF,L5=31.73 nH,C7=5.88 pF,L6=50.91 nH,C8=5.1 pF,C9=2.82 pF,L7=36.64 nH。 采用AWR Design Environment 仿真软件对基本电路和带两个传输零点的最终电路进行仿真,其仿真波形对比如图6所示。 根据仿真波形可知,相对三阶基本电路的频率响应,带两个传输零点电路的频率响应曲线其高端阻带抑制明显更为陡峭,且通带损耗变化很小。本方案在理论上实现了低插损、高陡峭度的高性能滤波器件的设计,且整体电性能完全满足技术指标的要求。 图6 基本电路与带两个传输零点电路的仿真波形对比 按照上述方案设计的拓扑电路,实际制作了滤波器并进行了高低温试验的电性能测试,实测波形曲线见图7。 图7 滤波器实测波形 根据实测波形曲线图分析可知,实际制作的滤波器电性能特性与设计仿真结果非常吻合。在制作时合理地选用元器件及良好的散热设计,滤波器亦能承受120 W的输出功率,并根据用户使用后的反馈信息表明,滤波器完全满足了技术指标的要求,说明该设计方案切实可行。 本文通过对传统Chebyshev滤波器的研究和改进,提出了一种新型的“准椭圆函数”LC带通滤波器设计方法。设计中通过灵活引入有限传输零点而不用增加滤波器阶数来提高通道的选择性,并可以得到非对称的特定频率响应。多次工程实践证明,该设计方法具有较好的可行性和实用性,不失为高性能LC滤波器设计的良好选择。 参考文献: [1] 龚文斌,南伟.一种新型高性能LC带通滤波器的设计[J].电讯技术,2008,48 (5):112-114. GONG Wen-bin,NAN Wei.Design of a New High Performance LC band-pass Filter[J].Telecommunication Engineering,2008, 48(5):112-114.(in Chinese) [2] 强锐,王蕴仪. 准椭圆函数滤波器原型电路参数的优化提取[J].微波学报,2002,18 (3):18-22. QIANG Rui,WANG Yun-yi.The Optimization Method to Extract Quasi-Elliptic Filter Prototype Circuit Parameters[J].Journal of Microwaves,2002,18 (3):18-22.(in Chinese) [3] 森荣二.LC滤波器的设计与制作[M].北京:科学出版社,2006. SEN Rong-er.The Design and Production of LC Filter[M].Beijing:Science Press,2006.(in Chinese) [4] 黄席椿,高顺泉.滤波器综合设计法原理[M].北京:人民邮电出版社,1977. HUANG Xi-chun, GAO Shun-quan.The Integrated Design Principles of Filter[M].Beijing:The People′s Posts & Telecom Press,1977.(in Chinese) [5] TOMAS J B. Cross-Coupling in coaxial cavity filters-a tutorial overview [J]. IEEE Transactions on MTT, 2003, 51(4):1368-1376.
2.3 新型带通滤波电路的最终设计
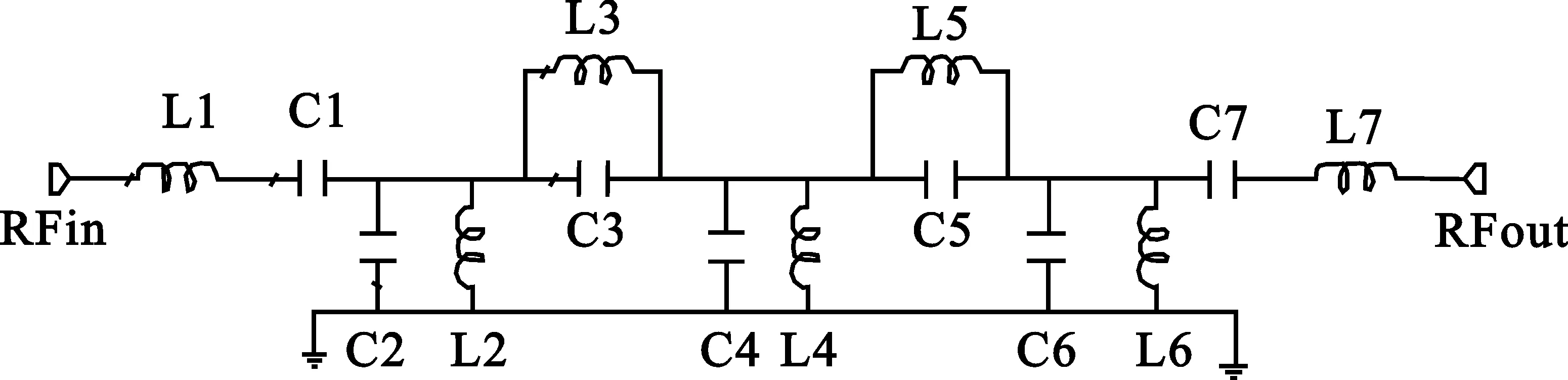
3 实例设计
3.1 滤波器主要技术指标
3.2 电路分析、设计及仿真
4 试验结果与设计仿真的比较
5 结束语

