圆形阵列天线方向图的分布函数优化方法*
赵万春1,师 君
(1.中国人民解放军驻157厂军事代表室,四川 彭州 611930;2.电子科技大学 电子工程学院,成都 610054)
1 引 言
阵列理论广泛应用于雷达、声纳及通信等领域,天线方向图[1-3]描述的阵列天线的分辨率特征是阵列天线设计的重要指标之一。数学上,天线方向图的分析可看作带参数的振荡积分的求解问题。但是,由于振荡积分相位函数具有多样性,可能为连续函数、周期函数或随机函数,该振荡积分的求解较为困难。目前,方向图的优化主要采用基于统计模型的优化方法,如模拟退火算法(SA)[4-8]及遗传算法(GA)[9-13]等。虽然上述方法可以对天线旁瓣进行优化设计,但无法揭示天线阵元布局与方向图之间的直接联系。另外,对于高维阵列,当天线阵元数目较多时,上述方法运算量较大。
在实际工程中,阵列天线阵元的数目有限,振荡积分的求解问题可近似为离散有限长复指数和的计算。通过引入分布函数的概念,本文介绍了离散有限长复指数和的计算方法,并将该方法应用于二维阵列天线方向图的分析,揭示了二维阵列天线阵元布局与其方向图的对应关系。然后,利用该关系分析了满阵圆形阵列、稀疏圆形阵列及混合圆形阵列的布局与天线方向图的关系,验证了该分析方法的正确性。
在上述研究的基础上,本文进一步分析了加权对天线方向图的影响,并在此基础上提出了一种基于分布函数的圆形阵列方向图优化方法。该方法通过对不同半径阵元权重的设计使得其对应的天线方向图达到与期望的窗函数相近的效果。
2 离散有限长复指数和的计算
阵列天线方向图优化问题数学上可以看作是振荡积分求解问题,由于该问题分析较为复杂,目前主要采用驻定相位原理进行近似求解。但是对于离散有限长信号,其指数和的计算可以采用本节给出的方法进行计算。
假设已知离散有限长信号f(n)=(0,1/4,2/4,0,1/4,1/4),需求解该信号的复指数和,其公式可表示为
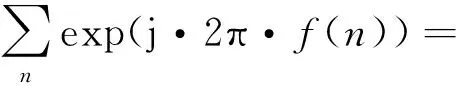
ej·2π·0+ej·2π·1/4+ej·2π·1/4
(1)
根据加法的交换律和结合律,式(1)可改写为
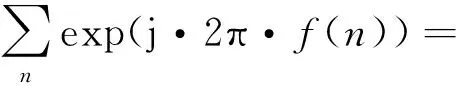
1·ej·2π·2/4+0·ej·2π·3/4(2)
式中,系数2、3、1和0表示各复指数项出现的频率(概率意义上)。因此,通过引入密度(分布)函数D(i)={2,3,1,0}的概念,可得到:
(3)
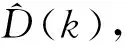
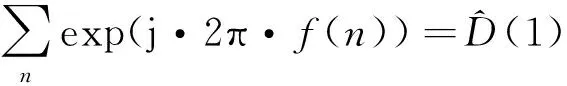
(4)
类似地,带有参数的离散有限长复指数和可表示为
(5)
根据上面的例子可看出,带参数的离散有限长复指数和可通过对其分布函数进行傅里叶变换得到,该性质为本文提出的圆形阵列方向图优化方法的技术。实际上,采用Lebesgue测度等方法,该性质可很容易地扩展到连续函数的振荡积分的计算。由于离散有限长复指数和的性质已经满足阵列优化问题的需要,连续函数的振荡积分将在其它的研究中详细论述。
3 阵列天线方向图
天线方向图是阵列天线的重要指标,反映了天线辐射电磁波在空间中的分布情况。阵列天线设计的一个关键问题为通过对阵型、阵元布局及权重系数的优化以获得期望的天线方向图。本节将利用上节介绍的计算方法推导二维阵列天线的方向图,并分析几种典型圆形阵列的方向图。
3.1 信号模型
二维阵列天线的几何关系如图1所示。

图1 阵列天线几何结构
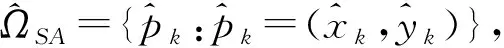
假设阵元中心相对目标中心的位置为
(6)
式中,x0、y0和z0表示该位置在x轴、y轴和z轴的分量。则二维阵列相对目标中心的位置可表示为
(7)
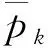
(8)
式中,ΩSA描述了二维阵列天线相对观测场景的位置。
(9)
(10)
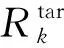
通过接收系统去载波处理,则阵列天线的接收回波可表示为
(11)
式中,λ为载波波长。
3.2 方向图
利用上节建立的信号模型,二维阵列天线的方向图可表示为

(12)
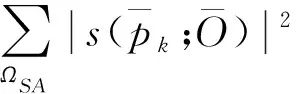
(13)
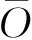
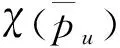
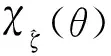
(14)
(15)
θ≜r/R0
(16)
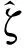
(17)
根据式(8),有:
(18)
则式(17)可写为
(19)

(20)

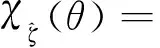
(21)
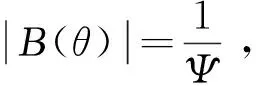
(22)


图2 二维阵列与方向图的关系
对于圆形阵列,由于其阵列关于圆形对称(或在统计学意义上对称),其任意方向的一维方向图可完全描述该阵列的二维方向图。
3.3 混合圆形阵列分析
上一节建立了任意阵列天线阵元布局和其对应的天线方向图的对应关系,该对应关系可用于分析各种平面阵列的方向图。由于篇幅所限,本节以混合阵列为例,说明该方法的有效性。混合阵列[14]是一种新型阵列天线结构,本文将考虑一种较为简单的混合圆形阵列,即阵列中部为满阵子阵列,周围为稀疏环形阵列,如图3和图4所示。
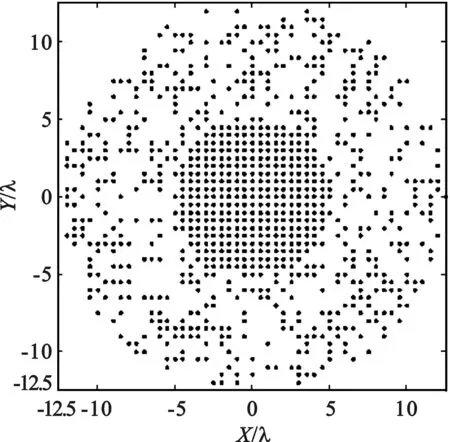
图3 混合圆形阵列
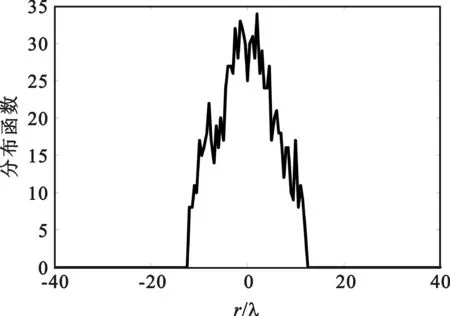
图4 混合圆形阵列分布函数
图4为混合圆形阵列天线的方向分布函数。可以看出,该分布函数可看作某窗函数被噪声调制后的结果,该窗函数可在一定程度上降低方向图的旁瓣,而噪声则在天线方向图中引入了随机性。图5为混合圆形阵列天线的二维方向图与一维方向图,其峰值旁瓣比和积分旁瓣比分别为-21.77 dB(存在随机性)和-15.45 dB。而圆形满阵元阵列的其峰值旁瓣比和积分旁瓣比分别为-15.87 dB和-13.94 dB。因此,混合圆形阵列可在一定程度上降低圆形阵列的旁瓣,达到节省天线阵元并优化阵列天线的方向图的目的。
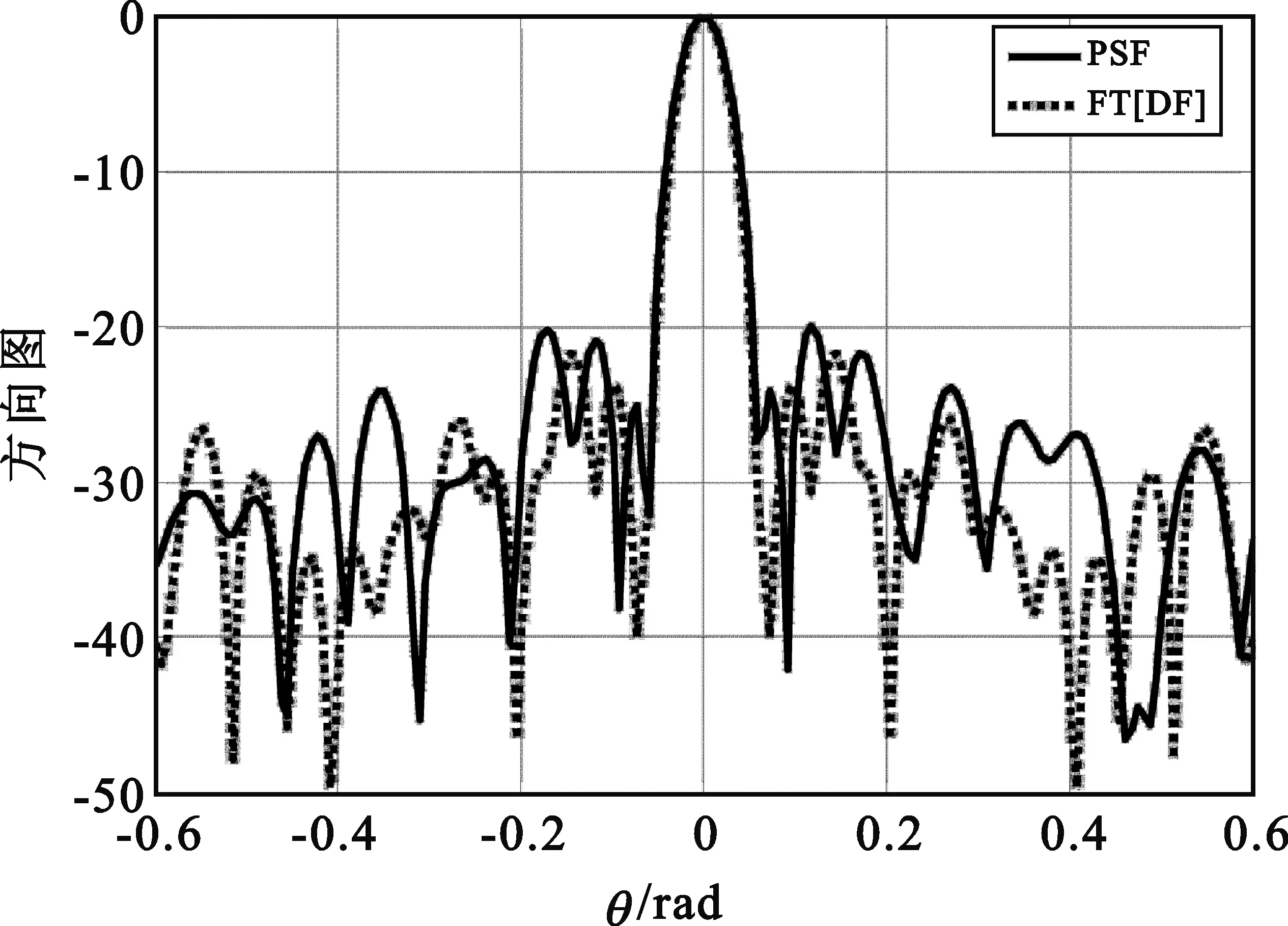
图5 混合圆形阵列某方向的方向图
4 基于分布函数的圆形阵列优化
根据上面的分析可以看出阵列分布函数与方向图存在对应关系,因此,可通过对分布函数的设计实现对方向图的优化。进一步分析表明,通过阵元分布优化对方向图的优化效果与改变阵元权系数对方向图的优化效果等效。本节将通过对阵列系数的设计实现基于分布函数的圆形阵列优化。
4.1 权系数对方向图的影响
(23)
相应地,其方向图可表示为
(24)
假设所有权系数均为自然数,则式(24)可表示为
(25)
该公式的物理意义如图6所示,表明在某个阵元上调制权重系数w相当于在该位置放置w个权重系数为1的阵元。
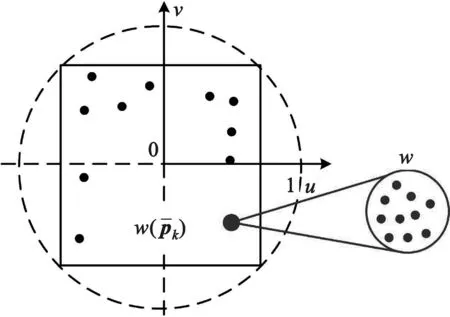
图6 权系数对方向图的影响
当权重系数为正实数时,通过将式(25)乘以某个足够大的正实数,并对所有权重系数进行取整近似,可很容易地将上述结论扩展到正实数的情况,即改变权重系数即可改变阵列天线阵元的等效分布。另外,与改变阵元数目相比,加权的方法可为任意正实数,更便于设计实现。下面将给出一种基于分布函数的圆形阵列天线优化方法。
4.2 基于分布函数的优化方法
由于圆形阵列关于圆点对称,如果其权系数也关于圆点对称,则其方向图关于圆点对称,此时,只需对其一维方向图优化即可实现对该圆形阵列的优化。因此,本文假设其权系数关于圆点对称,即其为半径的函数r,而与角度无关θ。
假设该权重函数为w(r),则加权累积函数的积分(即加权分布函数的积分,其关系于概率密度函数和概率累积函数的关系近似)Cwf(y)可表示为
显然,Cwf(y)对应的加权分布函数为偶函数。
为了实现对圆形阵列的优化,可通过对权重系数w(r)的设计,使得其对应的加权分布函数满足特定的窗函数,即:
(28)
式中,ω(u)为期望的窗函数,如汉明窗、Chebyshev窗等。
由于Cwf(y)为偶函数,只需考虑y≤0的情况,则式(28)可表示为
(29)
为了求解权系数w(r),可将式(29)离散化为矩阵形式:
G·W=C
(30)
(31)
(32)
(33)
式中,W为离散化的权系数向量,C为离散化的期望窗函数,G为离散化的积分矩阵。则最优化权系数向量可求解为
W=G-1·C
(34)
式中,G-1为G的逆矩阵。
假设期望的窗函数为Chebyshev窗,其旁瓣高度为-70 dB旁瓣,可计算得到其对应的权系数。
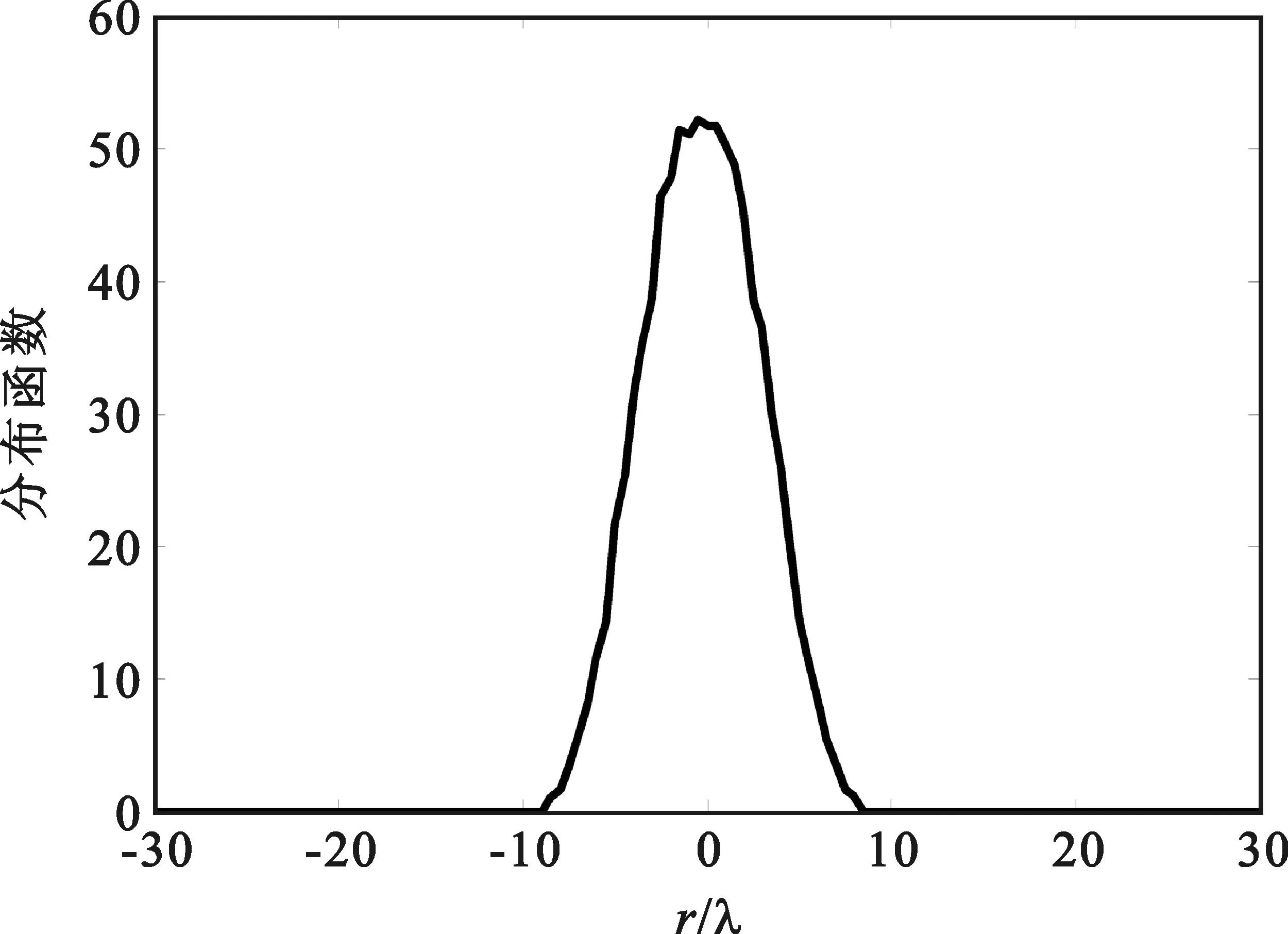
图7 优化加权分布函数
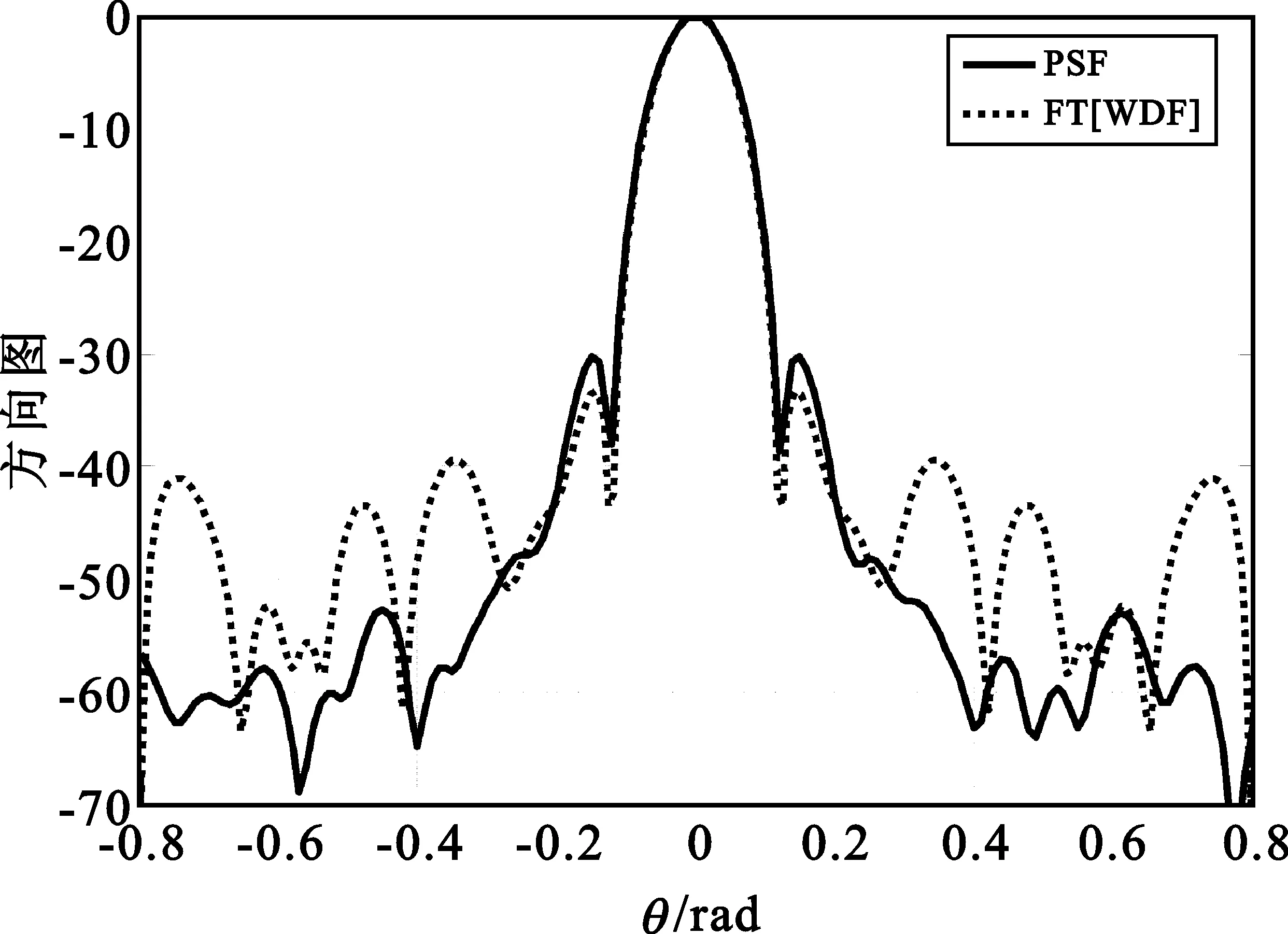
图8 一维方向图
从图7可以看出,其形状与Chebyshev窗函数较为相似。从图8可以看出,虽然该函数的峰值旁瓣比为-30.25 dB,高于Chebyshev窗(但优于前面分析的各种圆形阵列),但在第二旁瓣处出现了陡降,达到了将近-50 dB。另外,由于存在旁瓣的陡降,其积分旁瓣比为-30.44 dB,与峰值旁瓣比接近,要远远优于其它各种圆形阵列(如混合圆形阵列、圆形满阵元阵列等)。
5 结 论
通过引入分布函数,本文分析了二维阵列天线的方位图,可得到如下结论:
(1)二维阵列任意方向的方向图为其在该方向分布函数的离散傅里叶变换,该分布函数可通过统计其投影在某一方向的临近区域处阵元数目获得;
(2)该方法可较容易地分析各种二维阵列的方向图特征;
(3)通过改变阵元权重系数即可改变阵列天线对应的分布函数,进而改变该阵列天线的方向图,该方法与通过改变阵列天线阵元分布的方法等效;
(4)利用分布函数可实现对圆形阵列阵元权重系数的优化,使其近似满足特定的窗函数,从而大大改善圆形阵列的波束性能。
参考文献:
[1] Norton S J. Synthetic aperture imaging with arrays of arbitrary shape:Part I. General case [J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control,2002, 49 (4):399-403.
[2] Kozick R J,Kassam S A. Coarray synthesis with circular and elliptical boundary arrays [J]. IEEE Transactions on Image Processing, 1992, 1(3):391-405.
[3] Azevedo J A R,Casimiro A M E S. Non-uniform sampling and polynomial interpolation for array synthesis [J]. IET Microwaves,Antennas & Propagation,2007,1(4):867-873.
[4] Trucco A,Murino V. Stochastic optimization of linear sparse arrays [J]. IEEE Journal of Oceanic Engineering, 1999, 24(3):291-299.
[5] Trucco A. Thinning and weighting of large planar arrays by simulated annealing [J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,1999,46(2):347-355.
[6] Ferreira J A,Ares F. Pattern synthesis of conformal arrays by the simulated annealing technique [J]. Electronics Letters,1997,33(14):1187-1189.
[7] Trucco A. Synthesizing asymmetric beam patterns [J]. IEEE Journal of Oceanic Engineering,2000,25(3):347-350.
[8] Bevelacqua P J,Balanis C A. Optimizing Antenna Array Geometry for Interference Suppression [J]. IEEE Transactions on Antennas and Propagation, 2007, 55(3):637-641.
[9] Petko J S,Werner D H. The evolution of optimal linear polyfractal arrays using genetic algorithms [J]. IEEE Transactions on Antennas and Propagation,2005,55(11):3604-3615.
[10] Bray M G,Werner D H,Boeringer D W,et al.Optimization of thinned aperiodic linear phased arrays using genetic algorithms to reduce grating lobes during scanning [J]. IEEE Transactions on Antennas and Propagation, 2002,50(12):1732-1742.
[11] Allard R J,Werner D H,Werner P L. Radiation pattern synthesis for arrays of conformal antennas mounted on arbitrarily-shaped three-dimensional platforms using genetic algorithms [J]. IEEE Transactions on Antennas and Propagation, 2003,51(5):1054-1062.
[12] CHEN Ke-song,YUN Xiao-hua,HE Z,et al. Synthesis of Sparse Planar Arrays Using Modified Real Genetic Algorithm [J]. IEEE Transactions on Antennas and Propagation, 2007, 55(4):1067-1073.
[13] Ares-Pena F J,Rodriguez-Gonzalez J A,Villanueva-Lopez E, et al.Genetic algorithms in the design and optimization of antenna array patterns[J]. IEEE Transactions on Antennas and Propagation, 1999,47(3):506-510.
[14] Wilson M J,Mchugh R. Sparse-periodic hybrid array beamformer[J]. IET Radar, Sonar & Navigation, 2007, 1(2):116-123.

