利用累积量和似然特征的卫星单-混信号调制识别算法*
廖灿辉,2,万 坚2,周世东
(1.清华大学 微波与数字通信国家重点实验室,北京100084; 2.信号盲处理国防科技重点实验室,成都 610041)
1 引 言
通信信号调制识别是盲接收领域里的一个重要研究课题[1]。随着通信技术的发展,尤其是各种新调制方式的不断出现,调制识别方法需要不断发展以适应日趋多样化的识别要求。
传统卫星通信一般采用常规调制信号,常用调制方式有BPSK、QPSK、8PSK和16QAM 4种。1998年,ViaSat公司提出了应用于卫星的成对载波多址(PCMA)技术[2],通过在同一频点上发送两个同调制信号来进行通信,因此通信信号是两个同调制信号的叠加,常用的叠加方式有QPSK叠加、8PSK叠加和16QAM叠加。PCMA技术的应用使得传统卫星调制识别增添了新的内容,即除了识别常规调制信号的调制类型外,还需要识别是否是PCMA信号,以及属于何种调制混叠的PCMA信号。
目前,调制识别主要有判决理论和统计模式两种途径,前者比较复杂,后者容易实现。本文采用后者,旨在找到一种不需要知晓定时等先验信息、存在残余载波下仍能有效地对MPSK(M=2,4,8)、16QAM、MPSK混(M=4,8)和16QAM混进行识别的算法。信号的高阶累积量包含信号星座图信息,可以看作信号的一个签名[3]。本文将从高阶累积量出发,并结合似然特征,构造一个树形分类器来进行识别。
2 信号模型
接收信号的一般模型为:r(t)=s(t)+n(t),其中n(t)是加性高斯白噪声,s(t)是调制信号,具有如下形式:
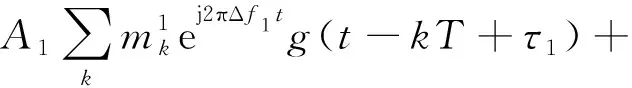
(1)
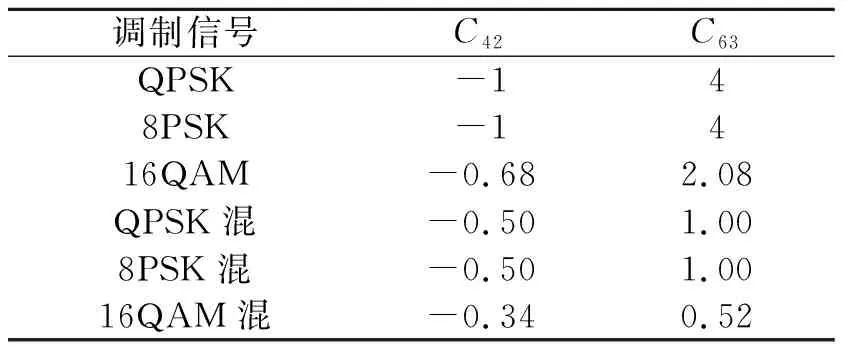
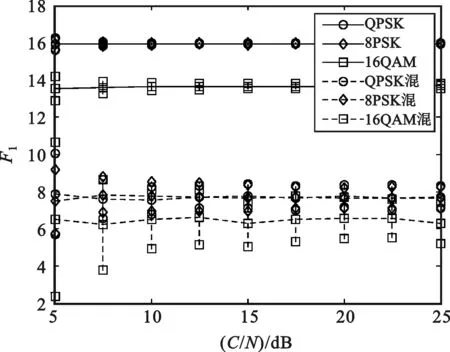
当s(t)是常规调制信号时,有A1≠0,A2=0;当s(t)是PCMA混叠信号时,考虑到两通信终端发送的功率相等,有A1=A2≠0。T是符号周期,Δfl(l=1,2)是残余载波,τl(l=1,2)是时钟偏移,假定0≤τl (2) i=0,1,2,…,M-1 (3) 数字信号处理的是r(t)经采样后的序列,记为rk=r(kTs),Ts是采样率。对于常规调制信号而言,进行调制识别时并不直接对rk进行处理,而是提取定时位置处的采样值。这是因为定时位置处的值消除了符号间串扰,包含了更多调制信息,用于调制识别将会取得更好的效果。考虑到接收信号有MPSK和QAM调制,进行定时估计时需要找到一种对这几类调制信号均适用的算法,而M.Morelli提出的开环定时估计算法[4]满足要求。 (4) 式中,L0是符号长度,N是过采样倍数。公式(4)是一种基于最大似然准则的估计算法,由最大似然原理可知,其计算出的定时位置是一个符号周期内信号能量最大的时刻。对PCMA混叠信号而言,用式(4)进行定时估计将会定位在两信号定时位置的中间。 信号的高阶累积量包含了信号的调制信息,且二阶以上的累积量能消除高斯噪声的影响,具有良好的抗噪声能力,因此常常被提取出来作为特征进行调制识别。文献[3,7]假定载波、定时同步时,通过提取高阶累积量特征来对MPSK信号进行识别;文献[8]将高阶累积量与高阶矩结合,利用神经网络来识别MPSK和MQAM信号。本文也将提取高阶累积量特征,除了能抑制高斯噪声、对MPSK和MQAM信号具有出色识别能力等优点外,还在于累积量具有下面一个性质,该性质应用在PCMA混叠信号上将会表现出不同于常规调制信号的特点,即若随机变量{xi}和{yi}统计独立,则累积量具有“半不变性”: cum(x1+y1,…,xk+yk)=cum(x1,…,xk)+ cum(y1,…,yk) (5) 式中,cum表示累积量。设接收信号单个符号间隔的平均能量为E,则对于常规调制信号而言,四阶累积量值正比于E2,六阶累积量值正比于E3;PCMA信号是相互独立的两个同调制信号混叠,每个信号单个符号间隔的平均能量为E/2,四阶累积量值正比于(E/2)2+(E/2)2=E2/2,六阶累积量值正比于(E/2)3+(E/2)3=E3/4。可以看出,PCMA混叠信号四阶以上累积量值与常规调制信号的累积量值不同,可用来区分这两类信号。 用Mpq代表信号的各阶矩,以样本xk为例,定义为 (6) 高阶累积量可通过高阶矩来计算,根据文献[9],有如下的换算关系: (7) 由于xk存在频偏,因此当p≠2q时,信号的调制特征将会被频偏所掩盖,有C20=C40=C41=0。C21、C42、C63不受频偏影响,其中C21表示信号的平均能量,可用C21对接收信号进行能量归一化。 表1给出了能量归一化下各调制信号定时抽样序列xk对应的C42、C63理论值。 表1 各调制信号抽样序列xk累积量的理论值 表1中混叠信号对应的累积量值是假定两信号定时位置相同时的计算结果。当定时位置不同时,定时序列xk不能消除符号间串扰,此时计算出的值相对表中值会有少许偏差。BPSK信号在有无频偏下计算出C42、C63不同,故表中未列出BPSK下的结果。 对于BPSK调制,其定时差分样本yk去除了频偏的影响。假定yk已进行能量归一化,对yk求二阶累积量有C20=1。对于其它调制信号,有C20=0,因此,选择特征C20能将BPSK调制与其余调制区分开。 在3.1节中,利用F1能将QPSK、8PSK与其余调制类型区分开,可选择差分样本yk对应的四阶累积量C40作为分类特征来区分QPSK调制和8PSK调制。从表2中知,对于QPSK有C40=1,而对于8PSK有C40=0。 表2 各调制信号差分序列yk累积量的理论值 对于PCMA类混叠信号,需要识别具体的混叠方式。可将QPSK混和8PSK混归为一类,16QAM混为另一类。从表1和表2中可以看出,这两类信号定时序列xk对应的C42、C63值不同,差分序列yk对应的C42、C63值也不同。这4个累积量值具有相似的区分度,可选择其中一个作为分类特征。 对于QPSK混和8PSK混,在存在频偏情况下,序列xk和yk对应的各阶累积量值均相同,不足以作为分类特征。文献[9,10]针对常规调制MPSK信号,从最大似然角度提取特征参量进行识别。对于QPSK和8PSK调制,该似然特征的近似计算式为 (8) 式中,rk是全采样序列,N是过采样倍数,L0是符号个数。该特征对QPSK混和8PSK混同样适应,不同的是,公式(8)针对的是无频偏信号,而本文考虑的是有频偏信号,因此需要对式(8)进行修改,如下: (9) 另外,在计算混合信号特征时,由于高次方的关系,交叉项的影响将会变大,从而提取出的特征相对于常规调制信号下的相应特征,区分度会变小。 图1 特征F1随载噪比的变化曲线 图2 树形调制识别框图 本节对图2所示识别算法进行计算机仿真。由于图2算法是基于累积量的,而累积量计算需要较长的数据,我们取数据长度L=4 000符号。载噪比范围取5~25 dB,步长2.5 dB,每个载噪比处进行500次Monte-Carlo实验。信号1的归一化频偏为Δf1T=3×10-4,信号2的归一化频偏为Δf1T=4×10-4,两信号时延差τ1-τ2=0.4T。若产生常规调制信号,则选取信号1;若产生PCMA信号,选取信号1、2等幅相加。信道为高斯白噪声信道。 图3给出了各调制信号识别率随载噪比的变化。从图3可以看出,当C/N≥7.5 dB时,BPSK、QPSK、8PSK和16QAM调制信号的正确识别率大于90%,常规调制信号与混合信号能正确区分的概率大于95%,而各调制混合信号在C/N≥12.5 dB时,正确识别大于90%。 图3 正确识别率随载噪比变化曲线 可见,混合信号调制识别所需要的载噪比要比常规调制信号识别高5 dB以上,这是因为,混叠的两个信号间存在相互干扰,影响调制信号特征提取的除了信道噪声外还有这些干扰噪声,而且求累积量与似然特征时均涉及到高次方计算,对干扰噪声有放大作用,因此需要更高的载噪比条件才能实现正确识别。 本文针对卫星通信中常用调制信号和PCMA类混叠信号的调制识别问题进行了研究,提出了一种基于高阶累积量和似然特征的识别算法。该算法不需要知晓信号的定时等先验信息,对残余载波不敏感,在正常通信所需的载噪比下对PCMA这类新信号能准确识别。文中只考虑了卫星信道下的性能,对复杂噪声及衰落信道下的算法改进及性能分析有待更深入的研究,将是我们下一步工作的重点。 参考文献: [1] Polydoros A, Kim K. On the detection and classification of quadrature digital modulations in broad-band noise[J]. IEEE Transactions on Communication,1990, 38(8):1199-1211. [2] Mark D.Paired carrier multiple access (PCMA) for satellite communication[C]//Proceedings of Pacific Telecommunications Conference.Honolulu,Hawaii:[s.n.],1998:787-791. [3] Swami A, Sadler B M. Hierarchical digital modulation classification using cumulants[J]. IEEE Transactions on Communications, 2000, 48(3):416-429. [4] Morelli M, Andrea A N D, Mengali U. Feedforward ML-based timing estimation with PSK signals[J]. IEEE Communications Letters, 1997, 1(3): 80-82. [5] 韩刚, 李建东, 李长乐,等. 一种改进的基于累计量的MDPSK信号分类算法[J]. 电子学报,2004, 32(10): 1613-1616. HAN Gang, LI Jian-dong, LI Chang-le,et al. An improved classification algorithm of MDPSK signals based on cumulants[J]. Acta Electronica Sigica, 2004, 32(10): 1613-1616.(in Chinese) [6] Mustafa H, Doroslovacki M. Effect of carrier offset on the classification of phase shift keying modulation using the subtraction of two consecutive signal values[C]//Proceedings of ICASSP 2007.Honolulu,HI:IEEE, 2007: 1289-1292. [7] Yang S Q, Chen W D. Classification of MPSK signal using cumulant invariants[J]. Journal of Electronic, 2002,19(1): 99-103. [8] Huo L, Duan T D, Fang X Q. A noval method of modulation classification for digital signals[C]//Proceedings of 2006 International Joint Conference on Neural Networks.Canada:[s.n.],2006: 2435-2438. [9] Huang C Y, Polydoros A. Likelihood methods for MPSK modulation classification[J]. IEEE Transactions on Communication, 1995, 43(2-4):1493-1504. [10] 赵知劲,朗涛. 基于最大似然比准则的MPSK信号分类方法[J]. 电路与系统学报,2006, 11(2): 54-57. ZHAO Zhi-jin,LANG Tao. A classification method for MPSK signals based on the maximum likelihood criterion [J]. Journal of Circuits and Systems, 2006, 11(2): 54-57.(in Chinese)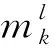
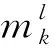
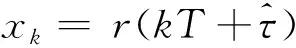
3 特征提取
3.1 分类特征1

3.2 分类特征2

3.3 分类特征3
4 识别框图
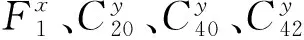
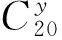
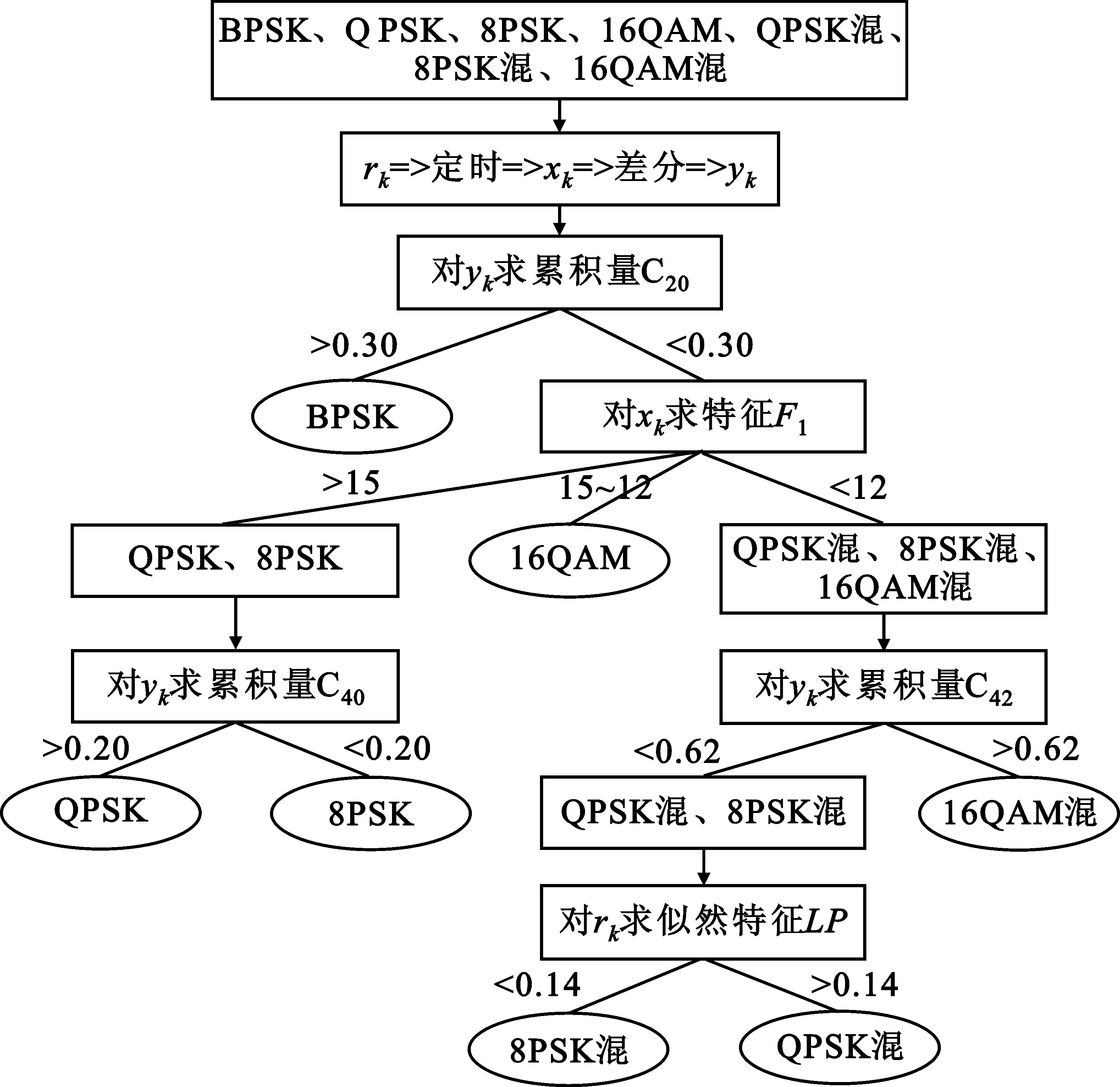
5 性能仿真

6 结束语

