采用偏心率和倾角矢量联合隔离法实现双星共位*
(解放军61081部队,北京100094)
1 引 言
随着航天技术的不断发展,气象卫星、导航卫星、通信卫星等在各自领域发挥了日益重要的作用。全球每年发射的卫星数量在不断增多,其中地球同步轨道卫星占有比例最高。根据国际电联相关规定,地球同步卫星的位置保持精度约为±0.1°,并且卫星之间需要保持一定的安全距离,因此地球同步轨道资源极为有限。然而,某些卫星由于工作频段需要,必须工作在特定的地球同步轨道位置区域,如果该特定区域已有卫星正在运行,新发射卫星就需要和已有卫星长期共位运行,在满足每颗卫星位置保持精度的前提下不能发生相互碰撞和相互遮挡。在国际上,多星共位技术比较成熟,双星共位较为普遍,最多达到五星共位。国内卫星共位技术正在不断成熟,但理论方法应用于工程实践还有许多问题需要解决。目前,工程实施上比较可行的方法有绝对偏心率隔离法、相对偏心率隔离法、偏心率矢量和倾角矢量联合隔离法以及经度隔离法等[1-2]。本文对偏心率矢量和倾角矢量联合隔离法进行双星定位的工程实践进行了论述,通过双星定位的成功实践能够验证该方法及控制策略的合理性和有效性。
2 偏心率矢量和倾角矢量联合隔离法
用于描述卫星轨道位置的主要参数[1-3]有:
平经度漂移率:D=-1.5(a-as)/as;

平赤经:L=Ω+ω+M;
式中,a为卫星半长轴,as为理想地球同步轨道半长轴,Ω为升交点赤经,ω为近地点幅角,M为平近点角。
为了避免两个卫星相互碰撞和相互遮挡,需要调整和控制两颗卫星之间的距离,使之始终大于安全距离,从而保证两颗卫星各自运行在安全可控的轨道范围之内。调整两星距离的手段主要是利用合理的卫星隔离方法制定工程上可行的卫星轨道控制策略,并分阶段实施,从而达到卫星轨控效果。卫星隔离的原理是将卫星之间距离分解为3个方向的距离分量,即径向距离分量、切向距离分量和法向距离分量,只要保证其中一个或一个以上距离分量大于安全距离的最低要求,即可保证两颗卫星的安全隔离。也可用偏心率矢量和倾角矢量来描述两星之间的距离,两颗卫星倾角矢量之差可用两星之间法向距离表示;两星偏心率矢量之差可用两星在径向和经度方向的距离表示。因此,卫星共位的前提是保持两星偏心率矢量之差和倾角矢量之差大于安全距离。
偏心率矢量和倾角矢量联合隔离法的基本思想是使两颗卫星的偏心率矢量差和倾角矢量差满足一定条件,即当两颗卫星在地球垂直赤道面的法向距离相等时,确保两颗卫星径向距离不相同,从而实现两星隔离。应用偏心率矢量和倾角矢量联合隔离技术时,应考虑两颗卫星的轨道特性、轨道测量和控制精度、允许控制频度(间隔多少天作一次东西保持控制、南北控制次数/年)、推进剂消耗量、控制策略修改限制及可扩展性、定点保持精度等主要因素[4]。
当两颗星在法向距离相等时,径向距离差可以表示成:
Δr=(a1-a2)∓asΔecos (φi-φe)
(1)
式中,φe、φi分别为相对偏心率矢量和相对倾角矢量的幅角;Δe为相对偏心率矢量的幅值;a1、a2、as分别为两颗星的半长轴和同步轨道的地心距。
此时联合隔离的条件可以表示成:
|Δr|=|asΔecos(φi-φe)|-|Δa|>d
(2)
式中,d为两星的径向隔离距离(约2 km),Δa为两颗星的半长轴之差。由于两颗卫星南北方向控制策略和东西方向策略不相同,相对倾角矢量的幅角变化很大,因此只能适当增大相对倾角矢量和偏心率矢量的幅值,以满足联合隔离的条件。
3 偏心率矢量和倾角矢量联合控制策略
3.1 倾角矢量控制策略设计
A星和B星的倾角矢量控制策略设计包括各自的倾角矢量初值控制、南北控制方向及倾角矢量控制等。A星在倾角矢量初值控制时,需要适当调整倾角控制时间,将倾角矢量控制到(-0.16°,-0.07°)附近。每次南北控制的倾角控制方向为
(3)

若控制前的倾角矢量为(ix,iy),则倾角矢量控制目标为
iyT=-0.07°
(4)
根据偏心率矢量和倾角矢量联合隔离的要求,B星倾角矢量控制要求为
ix>-0.02°
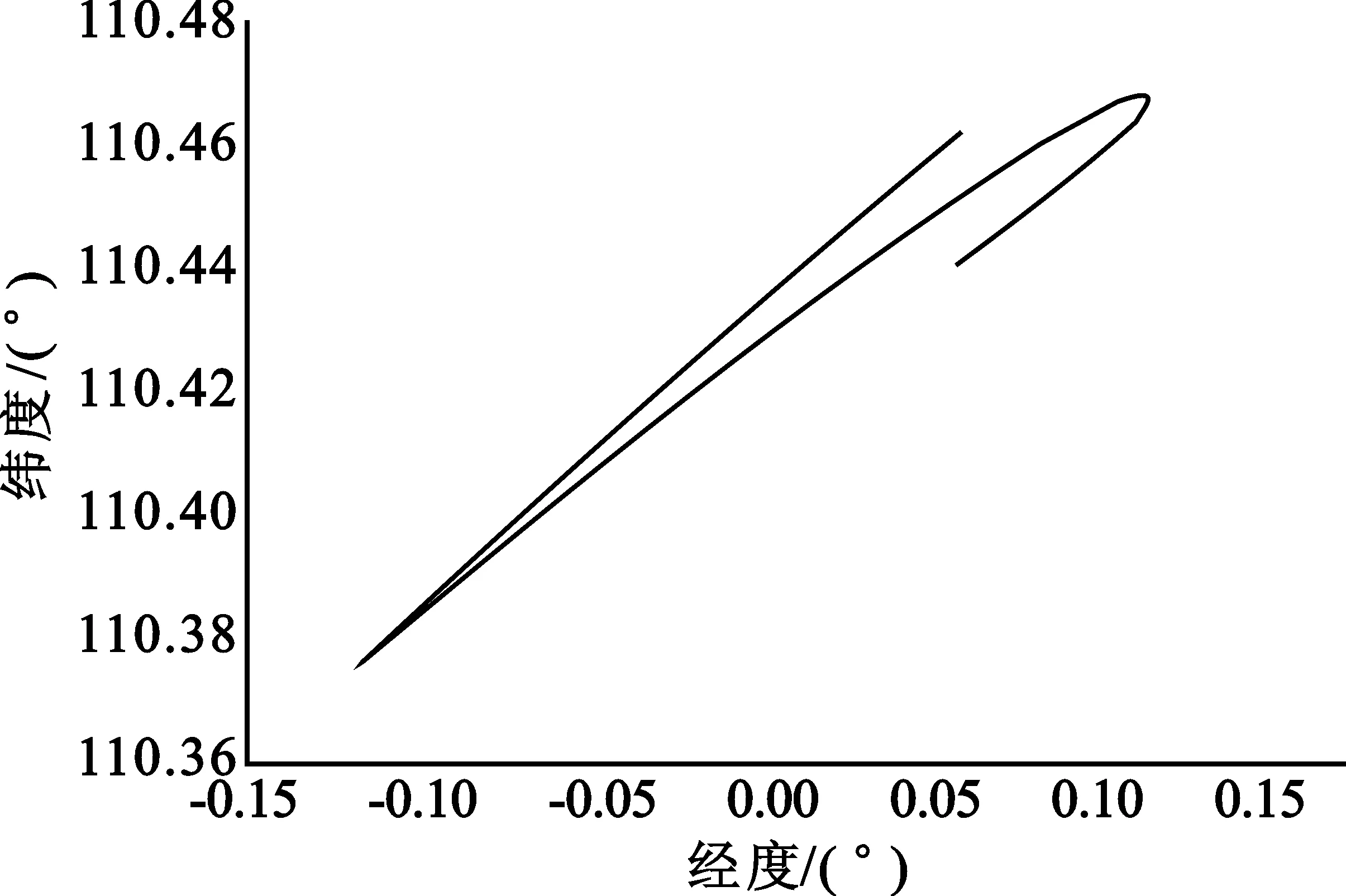
-0.1° B星每次南北控制的倾角控制方向与A星的倾角控制方向相同,即: B星若两个月不进行南北控制,倾角必然超过0.1°,在这种情况下可以每年进行2次或4次非最优时刻的南北控制,以提高南北控制精度。 根据上面的联合隔离参数,A星和B星共轨运行期间,希望两星的偏心率矢量沿某一特定的圆轨迹变化。但当偏心率初值不同时,偏心率摄动圆就不同。日月引力、地球非球形摄动、太阳光压会引起偏心率矢量周期性变化。另外,卫星东西位置保持和南北位置保持引起的东西耦合都会导致偏心率矢量变化。因此,相对偏心率矢量控制策略包括两颗卫星的偏心率矢量初值设置、东西位置保持过程中的偏心率矢量控制策略和南北位置保持后的偏心率矢量控制策略。 A星需要将平偏心率矢量控制到: eBx=eBxc+ec2cos (αs-β) eBy=eBxc+ec2sin (αs-β) (5) 式中,ec2=2.9×10-4为偏心率控后圆半径,αs为当天的太阳赤经,β=23°为偏心率矢量迟后太阳方向的角度。平偏心率矢量不包含各种日周期项和月亮引力引起的半月周期项。在正常情况下,偏心率矢量控制通过东西控制实现,传统的偏心率矢量控制采用双脉冲控制。为了减少东西控制量产生的总控制误差,因此偏心率矢量控制由双脉冲控制改为单脉冲控制。实际控制时,需要对计算出来的控制时刻进行限制,于是采用如下限制策略: 若L-αs>360°,则L取L-360°; 若L-αs<180°,则L取L+360°; 若L-αs>165°,则L=αs+165°。 (6) 当A星南北位置保持时对东西位置保持耦合影响比较大,可能需要进行多次东西位置控制,修正卫星的平经度漂移率和星下点位置以及控制卫星的偏心率矢量,此时偏心率矢量的控制目标同偏心率矢量初值设置。 为了适当提高两颗星的径向隔离距离,要求B星偏心率矢量控制时,适当考虑倾角的影响。根据前面的隔离原则,B星的偏心率矢量应满足如下条件: (7) 式中,ec=0.000 27为偏心率控制圆半径,β1=25°,Ki=0.000 5为倾角矢量对偏心率控制的影响因子。当B星的偏心率矢量的摄动圆半径为4.5×10-4,向西控制的标称时刻迟后太阳赤经75°左右,于是采用如下限制策略: 若L-αs>165°,则L=αs+165° (8) 为了实时监测在轨卫星的轨道位置用以评估双星定位的实施效果,需要利用卫星地面控制系统的多个地面标校站作为测轨站对卫星进行实时测轨。根据定轨几何需求,可利用分布于国内东部、西部和南部的多个测轨站对A星和B星进行实时测轨。平时,测轨站数据入站频率为5秒/次;卫星轨位保持期间,多个测轨站的测轨数据采样率可提高至1秒/次,可为测轨计算提供相当于平时5倍的测轨数据,以保证轨控期间卫星轨道计算精度。 在对A星和B星进行测轨时采用了3种不同的定轨计算方法:三站交汇的几何定轨法、两个站以上的卡尔曼滤波法和最小二乘法。几何定轨法是利用3个以上的已知点的观测,根据卫星和测站的几何关系,解算卫星观测瞬间的位置坐标。由于几何法可用来实时提供卫星的位置,因此在对卫星轨控期间,可以利用几何法实时计算卫星的轨道和预报短时间内的星历。卡尔曼滤波法即利用两个以上测轨站跟踪数据确定卫星轨道,该方法得到一组测距量,就完成一次轨道确定,适用于一个特定的测量周期内。根据卡尔曼滤波法的特点,在对卫星轨控前调整测轨站采样频率,输入卫星机动文件(时间、推力和推力方向)和卫星姿态及面质比,即可提供卫星的星历。卡尔曼滤波法和几何法在轨控期间并用,经轨道精度评估后选优。最小二乘法是用使卫星轨道的计算观测量和实际观测量的差的平方和最小的办法来确定卫星某历元时刻的位置速度与摄动(地球非球形引力场摄动、日月引力摄动、太阳光压摄动、潮汐摄动)模型参数。最小二乘法用于卫星轨控前和轨控后日常运行中的星历预报。系统根据卫星位置保持期间的不同状态分别采用几何法、卡尔曼滤波法和最小二乘法按照一定的策略完成卫星轨道计算。日常运行中,采用最小二乘法进行星历预报;轨道控制期间,采用几何法或卡尔曼滤波法实时计算星历,以保障轨控期间轨位计算精度。 为了直观体现双星共位的效果,可以利用双星共位运行后其中一颗卫星的星下点轨迹来表示。如果卫星星下点轨迹在位置保持控制精度范围内,即可表示卫星在正常轨道范围内运行。当两颗卫星都在保持相对距离不变的正常轨道范围内运行时,即可实现双星共位稳定运行。以A星为例,在共位试验中,其南北位置保持控制频度由三个月改为两个月;东西位置保持控制频度为半个月或一个月。A星在南北位置保持控制期间星历变化如图1和图2所示。图1表示第1次南北轨道控制期间的卫星星下点轨迹。由此可看出本次南北位置保持控制期间,卫星经纬度漂移范围是:东西方向为-0.08°~0.10°,南北方向为-0.17°~0.16°。图2表示最后1次南北轨道控制期间的卫星星下点轨迹。由此可看出本次南北位置保持控制期间,卫星经纬度漂移范围是:东西方向为-0.08°~0.11°,南北方向为-0.06°~0.14°。 图1 第1次南北位置保持期间卫星星下点轨迹 图2 最后1次南北位置保持期间卫星星下点轨迹 A星在东西位置保持控制期间星历变化如图3和图4所示。图3表示A星在共10余次东西轨道控制期间的某一次东西位置保持后的卫星星下点轨迹。由此可看出此次东西位置保持控制期间,卫星经纬度漂移范围是: 东西方向为-0.16°~0.13°,南北方向为-0.16°~0.17°。图4表示A星最后一次东西位置保持后的卫星星下点轨迹。由此可看出此次东西位置保持控制期间,卫星经纬度漂移范围是: 东西方向为-0.132°~0.034°,南北方向为-0.116°~0.117°。 图3 南北位置保持期间卫星星下点轨迹1 图4 南北位置保持期间卫星星下点轨迹2 综上所述,在近1年的双星共位试验中,A星的位置保持精度为东西方向优于±0.1°,南北方向优于±0.18°,满足B星东西方向优于±0.1°、南北方向优于±0.2°的精度要求。因此,无论是卫星南北位置保持后的卫星轨道还是东西位置保持后的卫星轨道都能证明卫星的位置精度满足双星共位要求,即利用偏心率矢量和倾角矢量联合隔离的方法能够有效地实现双星共位。 本文对偏心率矢量和倾角矢量联合隔离法进行双星定位的工程实践进行了详细论述,探讨了如何利用该方法制定合理可行的卫星轨位控制策略,并通过有效的卫星定轨方法进行双星共位效果评估。通过双星共位效果可以证明利用该方法制定的卫星轨位控制策略的有效性。双星共位的成功实践证明我国卫星共位技术已经从理论成果推进到了工程实践,今后将会有越来越多的卫星实现共位运行。卫星共位技术能够提升我国的卫星轨道控制能力,并为我国争取到更多的卫星轨道资源。 参考文献: [1] 石善斌,董光亮,罗强.两种静止轨道多星共位位置保持策略比较[J].上海航天,2009,26(2):55-60,64. SHI Shan-bin,DONG Guang-liang,LUO Qiang. The Comparison of Two Station-Keeping Strategies for Collocation of Geostationary Satellites[J]. Aerospace Shanghai, 2009,26(2):55-60, 64.(in Chinese) [2] 李建成,袁勇,王西京,等.基于绝对偏心率隔离的一点双星共位实现[J].西北工业大学学报,2006,24(1):1-4. LI Jian-cheng,YUAN Yong,WANG Xi-jing,et al. A Method of Collocating Two Chinese Geostationary Satellites with Two Eccentricity Vectors[J]. Journal of Northwestern Polyechical University, 2006,24(1):1-4.(in Chinese) [3] 张晓欣. 共位卫星距离分析[J]. 无线电工程, 2007, 37(12):43-45,48. ZHANG Xiao-xin. Distance Analyze of Common Orbit Satellite[J]. Radio Engineering of China,2007,37(12):43-45, 48.(in Chinese) [4] 戴光明, 王茂才. 多目标优化算法及在卫星星座设计中的应用[M]. 武汉:中国地质大学出版社, 2009. DAI Guang-ming,WANG Mao-cai. Multi-Objective Optimization Algorithms and its Application in Satellite Constellation Design[M]. Wuhan: Chinese Geology University Publishing House, 2009.(in Chinese)3.2 偏心率矢量控制策略设计
4 卫星定轨方法和实施策略
5 卫星共位效果评估



6 结束语

