多基地雷达马氏定位算法优化*

(海军装备研究院，北京 102249)

1 引 言

多基地雷达[1]的工作方式有一发多收、多发多收等模式，即使在受到强烈干扰或被反辐射导弹摧毁发射站后也可以在无源状态下工作，与单基地雷达相比，有较好的“四抗”能力，因此，对这种体制雷达的研究逐渐又成为了热点。但是，由于工作方式的不同，不能直接沿用单基地雷达的数据处理办法。文献[2，3]介绍了多基地雷达体制下数据处理的特点，并给出了一些通用的定位估计方法，文献[4-6]对具体定位估计方法进行了研究和改进。本文从定位数据分组及计算方式的角度，讨论了多基地雷达的马尔可夫估计定位算法优化问题，马尔可夫估计方法是加权最小二乘方法的一种最优解，即加权矩阵为测量噪声协方差矩阵的逆。这种方法目前多在双基地雷达体制下进行仿真实验，研究的也比较深入，这是因为双基地雷达的数据量不大，在仿真条件下，可以充分利用测量到的冗余信息提高定位精度。当应用到多基地雷达定位时，由于接收站增加，导致数据量增加明显，这种方法的缺点也体现出来：目标位置的计算方法、计算量增加，加权矩阵的求取比较复杂。本文从定位解的计算入手，对定位方法进行了简化，提出一种新的数据分组方法，即统一使用一种数据分组方式、一种定位方法解，这种方法在计算量及复杂度和定位结果上进行了折衷，在损失部分定位精度的情况下，提高了定位效率。

2 马尔可夫估计方法定位

2.1 算法实现

马尔可夫估计方法是一种比较简单的数据融合方法，充分利用测量信息的冗余来提高定位精度。首先，将测量数据分成若干个小的子集，要求每个子集都可以计算出目标的位置。在最小化估计误差的方差原则下，将得到的定位结果进行融合，考虑到测量信息(距离、角度)在数值和方差上的差异，使用加权方法进行平均。假设多基地雷达系统的配置为一发双收，发射站的观测为斜距RT和方位角θT，接收站的观测为ρi和θi，则将全部的6个数据分成(ρ1,θ1,RT)和(ρ2,θ2,θT)两组，分别得到定位结果，然后使用加权最小二乘方法融合。

由上面给出的数据组，定位方程为

(1)

(2)

式中，(x,y,z)、(xt,yt,zt)、(xi,yi,zi)(i=1,2)分别表示目标位置、发射站位置和接收站位置。

求解上述两个方程组得到滤波初值，加权最小二乘的观测方程为

Z=HX+V

(3)

式中，Z=[z1z2]T为上述两个数据组得到的定位解；X为估计的目标位置；V为测量噪声向量；H是系数矩阵，形式为H=[EE]T，E为三阶单位阵。

加权最小二乘的估计方程为

XWLS=[HTWH]-1HTWZ

(4)

当权阵W等于测量噪声协方差矩阵的逆时，有最小的估计误差，此时称为马尔可夫估计。V的协方差阵为

(5)

(6)

式中，Aii为上述定位方程组中目标位置对各观测值的偏导即雅克比矩阵，实际计算时，可以先计算各观测值对目标位置的雅克比矩阵，然后求其逆即可得到；Pij是第i与第j个测量数据组之间的误差协方差矩阵。

2.2 简化方法分析

可以看到，定位初值的计算还可以有其它很多组合方式，如(RT,θT,θ1)、(ρ1,ρ2,θ2)等。一发双收6个测量量的情况下，定位解计算的方式有9种，如果继续增加接收站将导致测量数据增加，使得通过数据分组计算目标位置成为对系统计算速度影响较大的问题。因此，有必要考虑简化数据分组的方法，达到减小系统开销的目的。本文考虑的是一种简化的数据分组方法。

新的数据组分配为(ρ1,θ1,θT)和(ρ2,θ2,θT)，即使用发射站相同的一个测量值进行定位。计算过程同上，重点讨论权矩阵的求取。由式(6)可知

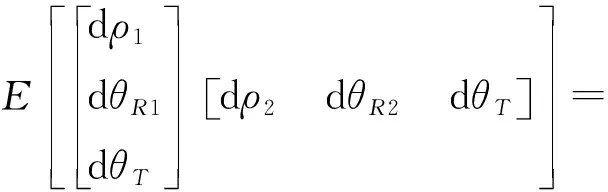
(7)

(8)

由计算可知，当测量子集有相同的测量信息时，P的行列式值为零，说明权矩阵不能取为测量噪声误差协方差矩阵的逆。同样方法可以证明，当定位初值计算使用(ρ1,θ1,RT)和(ρ2,θ2,RT)数据组时，P的行列式值为

(9)

(10)

式中，η表示发射站斜距与接收站距离和的相关系数，ηs表示各距离和之间的相关系数，由于相关系数η,ηs∈[0,1]，因此，行列式的值为负数，矩阵为负定。由于马氏估计方法的准确性，权系数矩阵的计算需要尽量靠近误差协方差矩阵，这时只能考虑改变RV的计算方法，为此，可把重复使用的观测数据看成两次独立观测数据，从而忽略其相关性，此时式(8)和式(9)分别变成式(11)和式(12)的形式：

(11)

(12)

重复使用发射站观测信息还有多种数据组合方式，如重复使用发射站距离观测信息的有[(ρ1,θ2,RT)，(ρ2,θ1,RT)]、[(ρ1,ρ2,RT)，(θ1,θ2,RT)]和[(ρ1,θT,RT)，(ρ2,θ2,RT)]等，重复使用发射站方位角测量数据的有[(ρ1,θ2,θT)、(ρ2,θ1,θT)]和[(ρ1,ρ2,θT)，(θ1,θ2,θT)]等，所有的组合方式都可通过上述的证明方法，得到一致的结论，但是由于其定位值的计算方法不具备普适性，因此不在此展开讨论。

3 仿真结果分析

本文对一发双收的多基地雷达系统进行了仿真，仿真计算时的参数设置为：发射站位置(xt,yt,zt)=(0,300 km,0)；两个接收站位置(x1,y1,z1)=(100 km,0,0)，(x2,y2,z2)=(-100 km,0,0)；测量噪声标准差σRT=2 m，σρ=20 m，σθT=σθ=0.001°；发射站的距离与接收站距离和的相关系数为η=0.2，距离和之间的相关系数为ηs=0.2；探测范围：X方向为±600 km，Y方向为±800 km，高度固定为1 000 km。

目标所在每一点上进行1 000次蒙特卡罗仿真。仿真结果为定位精度的GDOP(Geometrical Dilution of Position)曲线，即仿真图上线条数字，其计算式为

(13)

首先，给出单一的测量子集定为结果，图1和图2分别表示发射站和第一个接收站分别与第二个接收站的定位结果。图1使用的测量子集是(ρ1,θ1,RT)，图2 使用的测量子集是(ρ2,θ2,θT)。

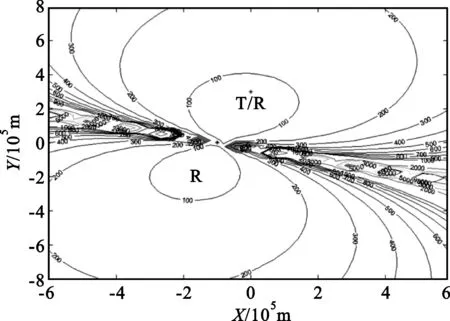
图1 T/R站与R1站的定位效果

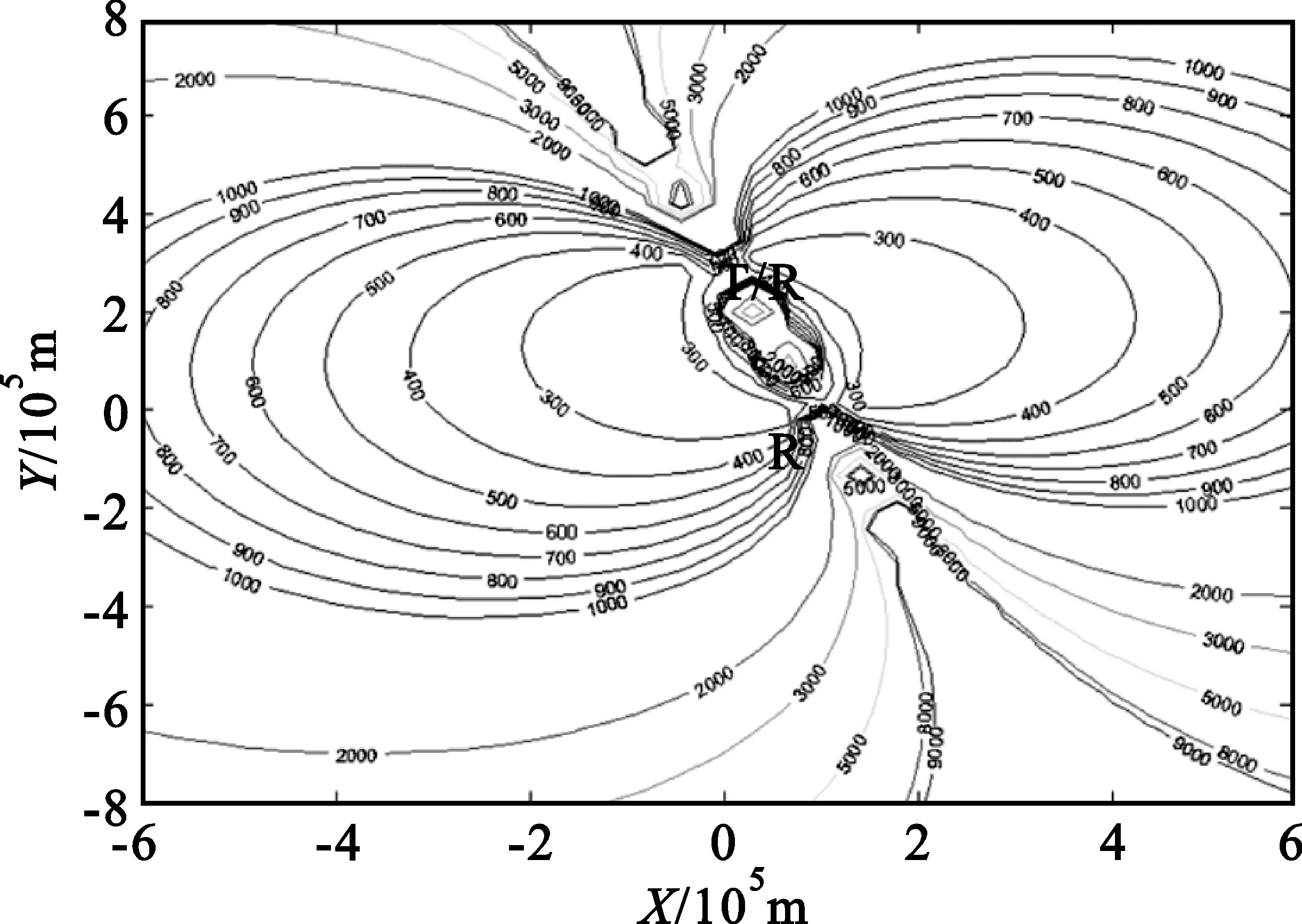
图2 T/R站与R2站的定位效果

图3使用马尔可夫估计方法进行定位，图4和图5分别采用数据组(ρ1,θ1,θT)、(ρ2,θ2,θT)和(ρ1,θ1,RT)、(ρ2,θ2,RT)进行定位。

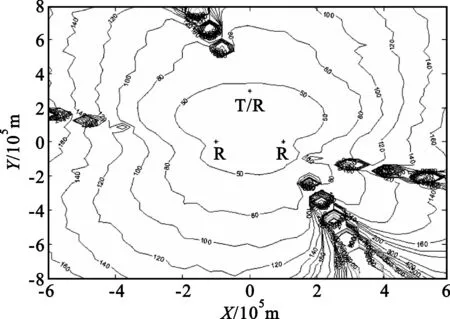
图3 马尔可夫方法的GDOP曲线

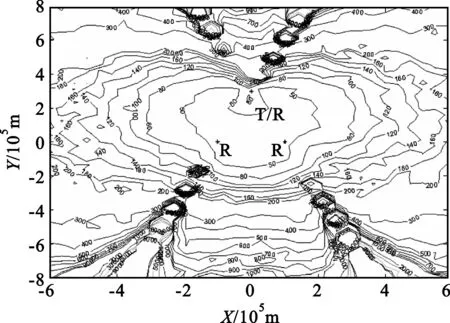
图4 共同使用发射站角度，优化方法

图5 共同使用发射站距离，优化方法

根据以上给出的仿真结果，对于加权最小二乘方法定位可以得到以下一些结论：

(1)对于双基地雷达，无论数据子集怎样选择都不能避免定位盲区的出现，其中基线附近是固有的盲区，这是双基地雷达一个基本特征；

(2)加权最小二乘及其改进的方法是将各数据子集的定位结果进行融合。仿真表明，也不能消除定位盲区，但是，可以使盲区的面积减小。并且，基线附近的定位精度提高非常明显；

(3)从定位效果上看，简化的方法要差于非简化方法，使用角度信息定位要差于距离信息定位，这是必然的，是由于省略了数据及改进了协方差矩阵造成的。当测量信息增加时，两种方法的差别会越来越小；

(4)当接收站继续增加，改进方法可以体现出计算上的优势，定位解可以统一使用发射站距离信息与接收站数据计算得到，通过简化计算方式进行融合处理，得到最终的定位数据。

4 结 论

总的看来，多基地雷达由于测量的数据量比较大，导致了其在定位方法上的选择较多，特别是当接收站数量持续增加时，组合方式增加迅速。本文从工程实现角度对马尔可夫定位方法进行了研究，该定位方法充分利用了测量量的冗余信息进行定位，精度较高，但在大数据量的情况下，数据分组解算方式也同时增加，增加了系统处理的复杂性。简化定位解分组舍弃了部分测量数据，提高了定位解算速度。通过对多基地雷达的仿真实验表明，定位精度没有明显下降，不失为一种有效的工程实用方法。

参考文献：

[1] Merrill I Skolnik.雷达手册[M].北京:电子工业出版社，2007.

Merrill I Skolnik. Radar Handbook[M].Beijing:Publishing House of Electronic Industry，2007.(in Chinese)

[2] 孙仲康，周一宇，何黎星.单多基地有源无源定位技术[M].北京:国防工业出版社，1996.

SUN Zhong-kang，ZHOU Yi-yu，HE Li-xing. Localization Technology based on Monostatic and Bistatic Radar System[M].Beijing:National Defense Industry Press，1996.(in Chinese)

[3] 刘淇.双基地系统探测及定位研究[D].长沙:国防科技大学，1998.

LIU Qi. Research on Detection and Location of Bistatic Radar[D].Changsha:National University of Denfense Technology，1998. (in Chinese)

[4] Farina A，Ehanle.Position Accuracy in netted Monostatic and Bistatic Radar[J].IEEE Transactions on Aerospace and Electronic System，1983，19(4)：513-520.

[5] 何友，王国宏，修建娟，等. 双/多基地雷达的组合估计精度及定位精度分析[J].电子学报，2000，28(3):17-20.

HE You，WANG Guo-hong，XIU Jian-juan，et al. Combinational Estimation and Location Accuracy Analysis in Bistatic/ Multistatic Radars[J].Acta Electronica Sinica，2000，28(3)：17-20. (in Chinese)

[6] 陈建春，丁鹭飞 多基地雷达最佳定位算法[J] 西安电子科技大学学报,1999，26(4):397-400.

CHEN Jian-chun，DING Lu-fei.Optimum position finding a lgorithm for multistatic radars[J].Journal of Xidian University，1999，26(4):397-400. (in Chinese)