中美初中统计与概率习题比较

金美月,贾 萍,张馨心

(1.辽宁师范大学数学学院,辽宁大连 116029; 2.大连市第三中学,辽宁大连 116033)

中美初中统计与概率习题比较

金美月1,贾 萍2,张馨心1

(1.辽宁师范大学数学学院,辽宁大连 116029; 2.大连市第三中学,辽宁大连 116033)

该研究通过 T检验等定量研究方法,从探究、背景、运算、推理和知识含量等五个因素上,横向比较了中美初中教科书中的统计与概率习题。结果显示,中美教科书中的习题在五个因素上均存在差异。最后,对中国初中统计与概率教科书习题编写提出了几点建议。

初中教科书;统计与概率;习题;中美

一、问题的提出

中国现行初中数学教科书与美国《情境数学》(Mathematics in Context)[1]的编写均体现了现实数学教育理念。《情境数学》在美国已经使用了十年之久,而且有一定的使用率,且得到了教师、学生和家长的一致好评。但由于文化背景、思维方式、社会发展以及地域的不同,即使基于相同的教育理念,编写出来的教科书也会出现一些差异。况且,统计与概率是此次课程改革中改动较大的部分之一。其中,作为中学数学课本中的重要组成部分,习题配备得好不好,直接影响到学生学习质量的高低。因此,本文通过人民教育出版社出版的初中数学教科书与美国《情境数学》进行统计与概率部分的习题比较,并对中国教科书建设提供一些建议。这里,习题是例题、练习题、习题及复习题等的总称。

二、研究方法

为了比较中美初中统计与概率习题,本文所研究的教科书有人教社的七年级 (上册) (2004年 4月第 1版)、八年级 (上册)(2004年 12月第 1版)、八年级 (下册)(2005年 10月第1版)、九年级 (上册)(2005年 10月第 1版);美国《情境数学》中的六年级:Dealing with data (数据处理)、七年级:Ways to Go(行进方式)、七年级:Statistics and Environment(数据与环境)、八年级:Digging Numbers(挖掘数字)、八年级:Insights into Data(深入数据)、八年级:Great Expectations(期望)。

习题主要从探究、背景、运算、推理和知识含量等五个因素[2]进行比较,而且,每个因素又划分为若干水平。各个因素及具体界定见表 1。

表 1 综合难度模型因素

人教版习题包括例题、练习题、习题以及每章后的复习题。《情境数学》中的习题包括正文中的习题和“总结”之后的 SummaryQuestions(总结问题)。由于数学题的解法不是唯一,为了有一个统一的标准,我们分析习题的运算及推理步骤时均使用了与教科书配套的教师用书。对于包含一个以上子题号的习题,有多少个子题号就算为多少道题。为了比较,首先分别计算两国的习题在每个因素水平上所占的百分率,然后采用 Z值双侧差异性检验 (α=0.05),若 Z＜=1.96则认为差异不显著,若 Z≥=1.96则认为差异显著。

三、习题比较

下面结合表 2,分别从探究、背景、运算、推理和知识含量等五大方面对中美初中统计与概率教科书中的习题进行比较。

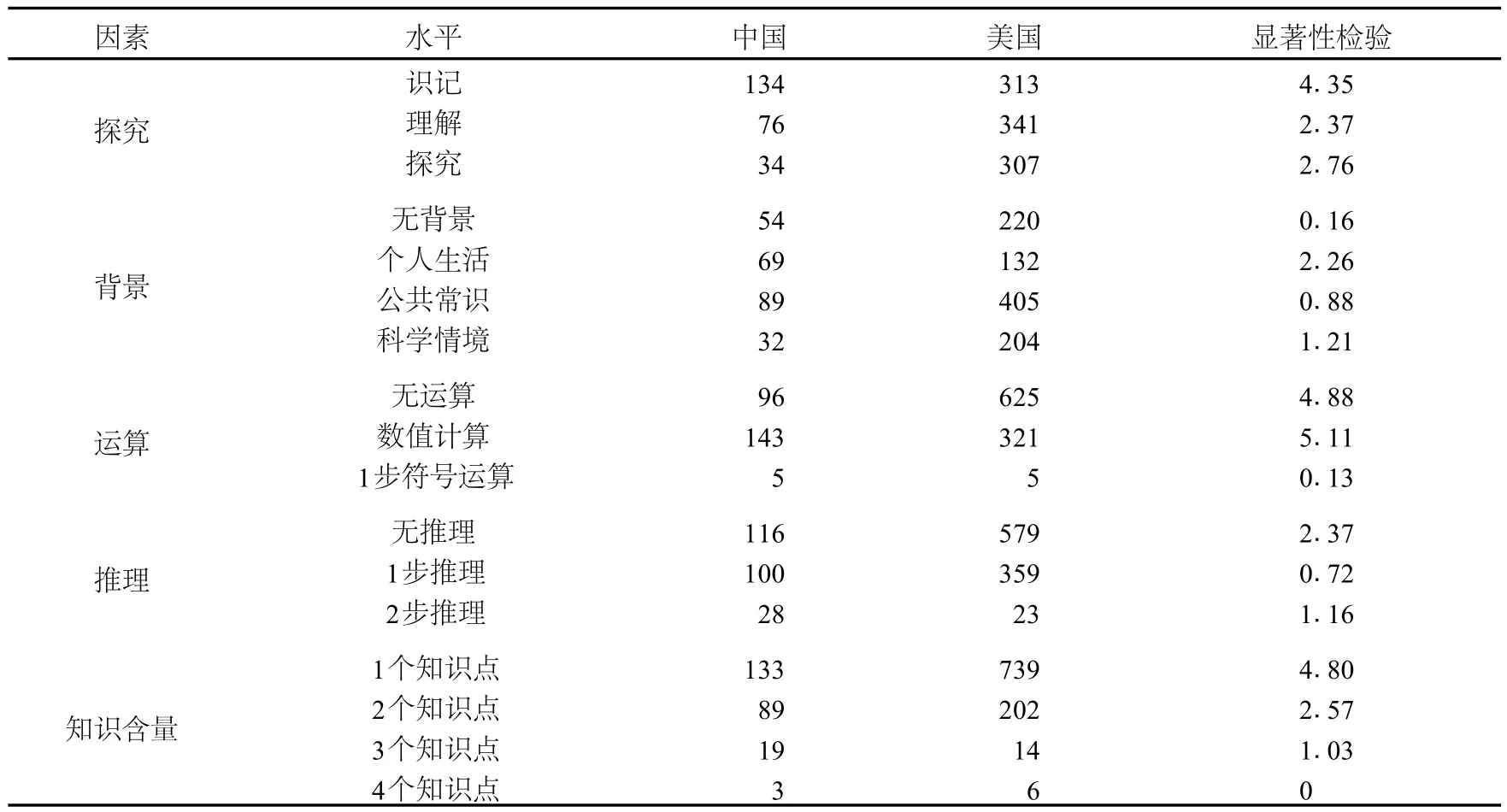
表 2 中美初中数学教科书统计与概率习题在各因素上的指标

(一)探究

如图 1所示,“探究”因素的三个水平分布上,美国教科书的折线图走势平缓,中国则明显呈下降趋势。这说明,美国习题的各个水平设置得比较均衡;中国则随难度水平的递增习题数目有相应的减少,从而表明侧重“识记”水平,对“探究”水平重视不够。

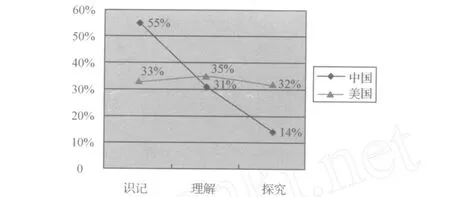
图 1 探究水平折线图

中美两国习题在“识记”水平上的显著性差异值为 4.35,百分率分别为 55%和 33%。这说明,两国在此水平上存在显著差异,进一步说明中国习题非常重视基本数学事实的记忆。

“理解”水平上,显著性差异值为 2.37,中美两国百分率分别 31%和 35%。这表明,美国更加注重学生对知识的理解。但是,通过中国七年级上册第 163页习题 4.2第 2题,美国《情境数学》八年级深入数据第 17页第 10题(由于篇幅,本文所举的习题内容全部给予省略)这两道例子我们可以得出,美国侧重于使学生深入理解概念知识的本质;中国则除了考察知识的本质之外,还注重该概念与其它相关知识的区别和联系,既强调知识的内涵,也强调它的外延。

在“探究”水平上,中美两国显著性检验结果为 2.76,百分率分别为 14%和 32%。这表明,两国存在显著差异,与美国相比,中国对探究水平的重视不够。这个结果不仅反映在两国习题的提问方式上,也反映在教师参考用书中的习题解答中。比如:中国教科书中普遍使用的习题提问方式为“用……做出……”,如,人教版八年级上册 61页练习题的第一题:“根据表12.1-3中的数据,分别用条形图和折线图描述这几年中国进出口总额 (进口额与出口额的和)的变化情况”,也就是说,题目很直接、明确地要求学生使用何种方法、哪个知识点,学生只要按照编写者的思路和要求去完成习题就可以,不需要从问题中自己挖掘相关数学信息,更不需要更深的探究;而美国教科书中最常用提问方式是“你从中能得出一些什么结论?”“选择一种你熟悉的方法”“你喜欢哪种方法”“解释你的做法”“说出你的理由”,这些表明美国非常重视学生的探究水平及合情推理。还有,中国教师参考用书中所给出的习题解答大部分是封闭、直接、明确的,可谓标准答案;美国的习题答案通常都是以“答案有多种”(Answerswill vary)开头,表现出因学生的探究水平不同所得出的答案会有所差异。

(二)背景

如图 2所示,背景因素的无背景、个人生活、公共常识、科学情境等四个水平的百分率上,中国教科书分别为 22%、28%、37%、13%,美国为 23%、14%、42%、21%;两国的折线图都以“公共常识”为最高点,不同的是美国以“个人生活”,中国则以“科学情境”为最低点表现出不同的趋势。表 2显示,两国习题只有在“个人生活”水平上存在显著差异,其显著差异值为2.26,其他三个水平上均无显著性差异。这些表明,两国都更加重视职业和公共常识背景,美国不重视“个人生活”,但是中国较强调“个人生活”。

尽管两国习题在“无背景”“公共常识”“科学情境”等三个水平上都不存在显著差异,但是通过分析教科书的具体习题设置就容易发现,美国教科书的每一个小节基本都包含一个情境,而且这些情境都比较丰富、生动。与美国教科书背景特点相比,中国稍显逊色,显得生硬。中国教科书为了增添背景,制造了一些真实程度有待商榷、与学生现实相去甚远、与数学知识无关联的人为制造的背景。

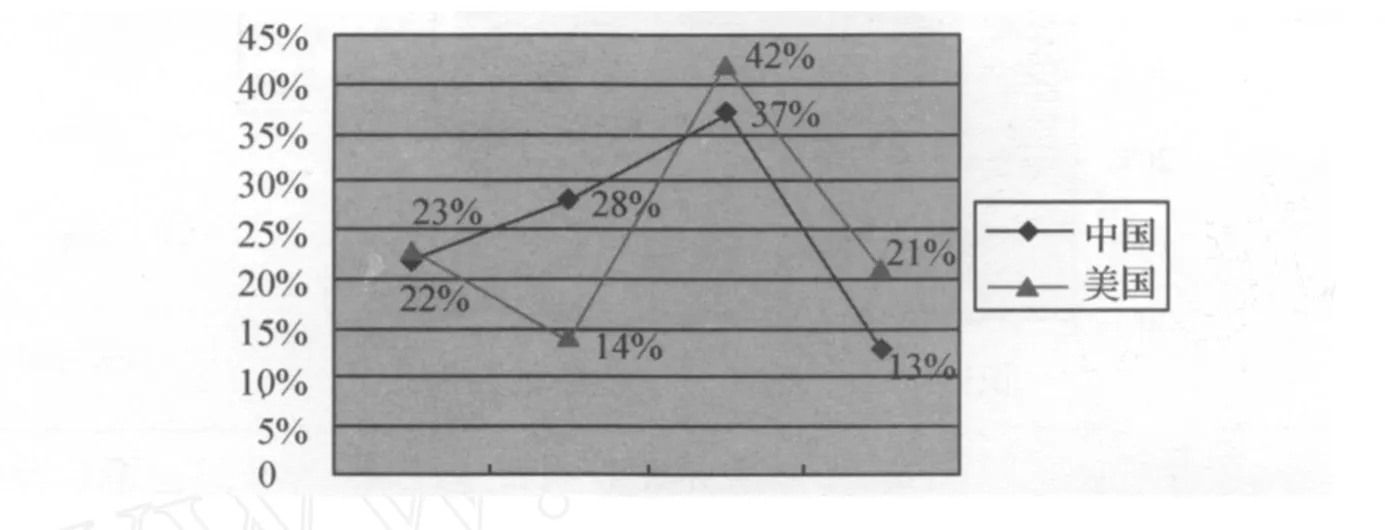
图 2 背景水平折线图

但是,中国教科书有一个亮点:即在习题的背景中较多地渗透了数学史知识。比如,八年级上册第 73页的习题不仅介绍了华人数学家丘成桐,还介绍了国际数学奖项菲尔兹奖。这类习题不仅为学生树立了榜样,激发学生的数学学习兴趣,而且在解决数学问题的同时,丰富了学生的社会常识。但是,美国教科书仅有一个章节涉及到历史,其情境是美国历届总统的就职年龄统计。

(三)运算

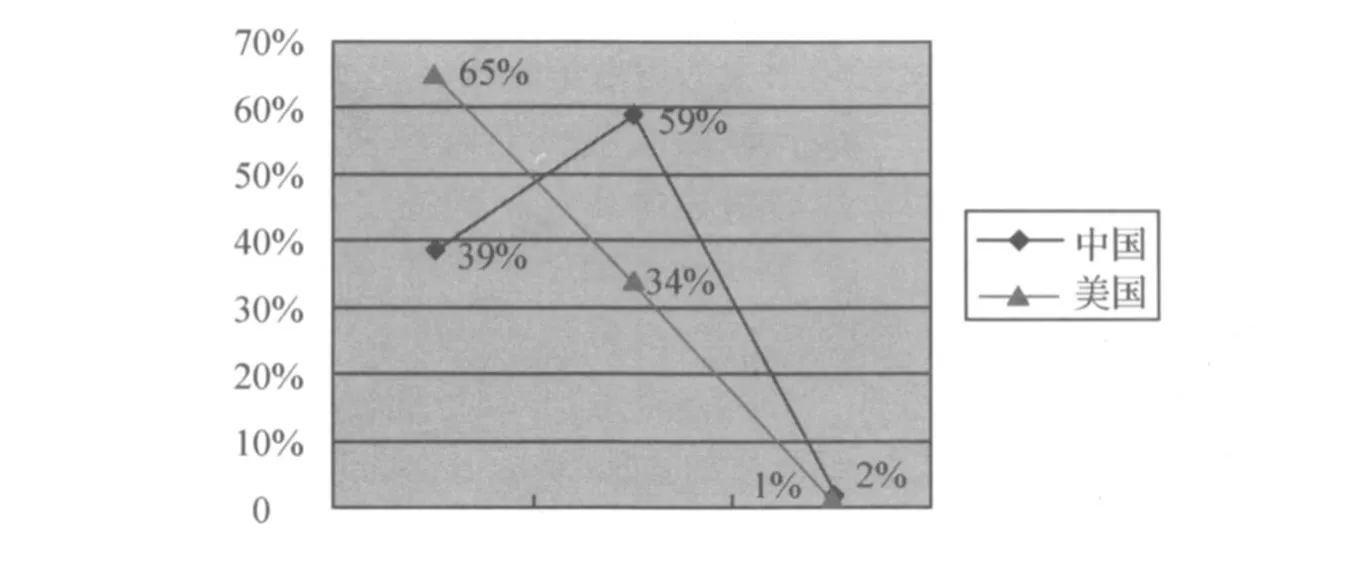
图 3 运算水平折线图

如图 3所示,运算因素上,中国习题的“数值计算”水平占 59%,明显高于其他两个水平。这说明,中国较强调计算,忽视符号运算。而且,其折线图呈现先上升后下降趋势;美国呈直线下降趋势,“无运算”和“符号运算”水平各占 65%和 1%。这表明,美国习题对运算的要求低,也不强调符号运算。表 2的显著性检验显示,两国在“无运算”和“数值计算”两个水平上存在显著差异,其值均大于 1.96。总的来说,中美两国都非常忽视符号运算;美国对运算的要求低,相反,中国则重视数值计算。

下面举中美两国教科书中关于算术平均数、众数、中位数三个平均数相关的具体运算习题,以此来剖析两国在运算习题设置上的差异。我们知道这三个平均数都是刻画一组数据的整体水平,但有其本质上的区别。算术平均数反映一组数据的平均水平,众数反映一组数据的多数水平,中位数反映一组数据的中间位置水平。尽管,这三个平均数的特点不一样,但常常容易混淆。因此,我们不仅要求学生掌握其各自的意义和作用,而且更加培养学生们根据不同的目的使用合理的平均数来进行刻画和描述一组数据。

中国人教版八年级下册168页复习题20第四题和《情境数学》六年级数据处理 24页的习题,都需要求出所给数据的三个平均数。但是,两国在这个习题上的要求却截然不同。中国习题仅仅要求学生直接计算这三个平均数即可。显然,学生通过这三个平均数的计算既不能深入理解它们之间的差异,也不能使学生感受各自的优劣,更不能做到用来解释实际问题。然而,美国习题设置则不同。它并不具体要求学生计算哪一个平均数,而是让学生选择支持自己观点的平均数。这需要学生不仅要掌握三种平均数的计算,更需要的是经过与情境相联系的判断做出选择合理的平均数。这需要学生从情境出发,经过数学思考,最终回到情境解决实际问题。从而很好地培养学生们利用所学平均数知识解决实际问题,掌握三个概念的本质,达到学概率统计的真正目的。

需要特别指出的是,本文在分析习题时将“估算”列为“数值计算”水平。估算是非严格意义上的运算,加强估算教学和提高学生的估算能力已成为国际数学教育改革的重要内容之一,而且中美两国标准都强调“估算”[3-4]。但是,中国教科书中鲜见估算的习题。美国则包含像“估计你的数学老师的头长是多少”“估算你手掌的宽度”“估计海鸦岛上的人均用水是多少”等估算习题,而且估算之后都会要求学生经过数据调查、分析来验证估算结果的正确性。

(四)推理

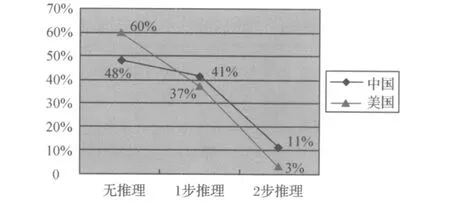
图 4 推理水平折线图

图 4显示,推理三个水平方面,两国均以“无推理”水平为最高点,呈下降趋势。表 2中,无推理、1步推理、2步推理的显著性检验结果分别为 2.37、0.32、1.16,表明两国在推理三个水平之中只有“无推理”水平存在显著差异。由此得出,中美均不强调多步骤推理。其中,美国不仅不重视多步骤推理,也不重视推理。中国习题则重视“1步推理”及“无推理”。

尽管,中国概率统计教科书较之美国更多强调推理,但通过分析两国习题,我们可以看到中国强调的推理中所缺乏的部分——猜想。如,美国《情境数学》八年级深入数据第 2页第 1题是让学生先预测问题结果,然后经过一系列数学知识的讲解之后再验证之前的预测。但是,中国教科书中我们很难发现有关“预测”“猜想”等习题。

(五)知识含量

如图 5显示,两国的折线图都以“1个知识点”为最高点,呈下降趋势,而且均没有设置包含 5个或者 5个以上知识点的习题。表 2表明,两国在“3个知识点”和“4个知识点”上不存在显著差异,在“1个知识点”和“2个知识点”上存在显著差异。这表明,中美两国的习题设置都非常不重视“3个知识点”以上的知识。其中,美国非常重视单个知识点,中国则非常重视单个及2个知识点。

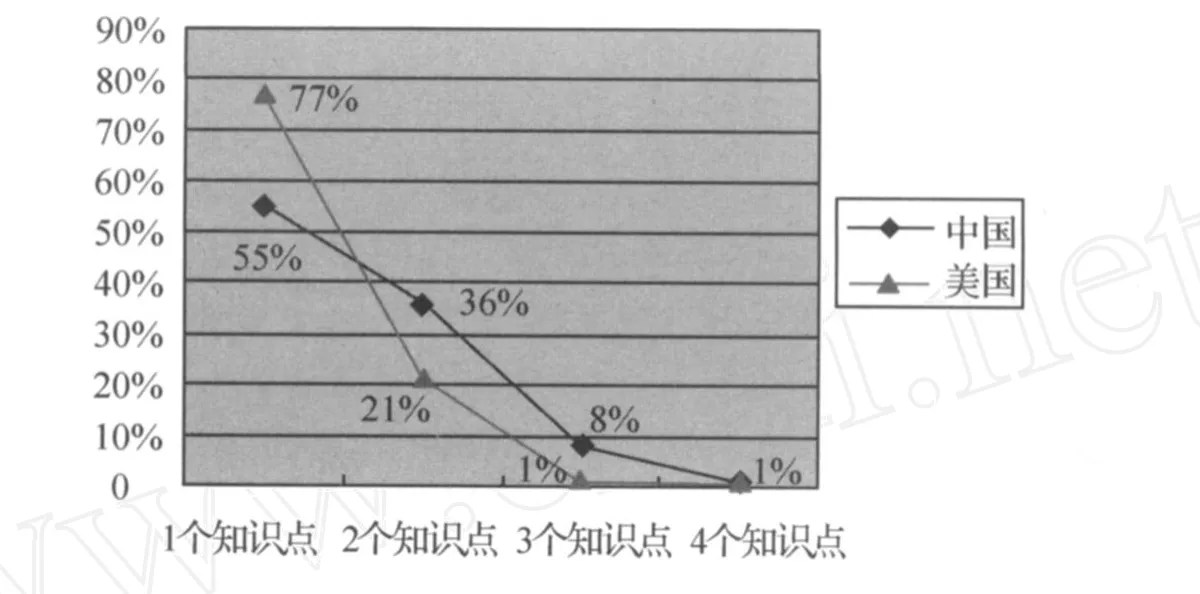
图 5 知识含量折线图

尽管,在“3个知识点”和“4个知识点”上两国习题不存在显著差异,但是由于这只是对知识点个数的统计比较,不能反映出其它重要信息。因此,通过分析两国包含相同知识点个数的相同数学内容的习题,挖掘其中的差异。如,人教版八年级上册 75页习题 12.2第 4题,《情境数学》六年级数据处理 C小节(Section C)的第 18题。

从题目要求来看,两道习题的目的都是想要学生掌握不同图表在表示数据时的优劣势,但是两国习题实际表示出的目的却存在很大差异。尽管中国的习题背景是“公共常识”,情境设置得也很好,但中国这道习题显示的目标是要求学生全面掌握这些所有图表知识,并不要求学生依情境进行判断、选择。从而,首先无法使学生学会选择适当的知识;其次,更不能实现学统计的真正目的——解决实际问题。而美国教科书的习题设计所显示的截然相反。美国概率统计教育的真正目的不在于使学生掌握如何画图表,而在于学会选择自己熟悉的、实用的方法来处理实际问题。这里,重要的是学生学会自己选择、自己做出合理判断。

四、结论与建议

(一)结论

根据上述分析,我们发现中美教科书的习题在探究、背景、运算、推理、知识含量等五个因素的各个水平上都存在一定程度的差异。

“探究”因素。中国习题停留在“识记”水平,而且比美国更重视基本数学事实的记忆。在“理解”水平上,美国重视概念本质的理解,中国除考查知识本质外,还注重与其相关知识之间的联系与区别。美国重视“探究”水平,中国则不然。

“背景”因素。美国习题不重视“个人生活”,中国则较强调;而且,中美都很重视职业和公共常识背景。尽管,两国在无背景、公共常识、科学情境等三个水平上都不存在显著差异,但是,美国教科书的每一个小节基本都包含一个情境,而且这些情境都比较丰富、生动;与美国教科书背景特点相比,中国稍显逊色、生硬,而且人为创设的背景痕迹明显,背景中信息的真实程度有待商榷。总的来说,美国教科书的情境创设较为合理,贴近学生现实;中国教科书中部分背景与数学知识无关联。不过,中国教科书有一个亮点,即习题背景中较多地渗透了数学史知识。

“运算”因素。中美两国都非常忽视符号运算。美国对运算的要求较低,但其习题设置重视概念的本质,培养学生从情境出发,经过数学思考,回到情境解决实际问题的能力,从而最终达到概率统计的教育目的。中国习题只重视数值计算,尽管仍保持传统的优势,但遗憾的是不能促进概念本质的理解,以及概念之间的联系与区别,更不能培养解释实际问题的能力。除此之外,美国习题强调估算,中国则不然。尽管,中美数学课程标准都强调“估算”,加强估算教学和提高学生的估算能力已成为国际数学教育改革的重要内容之一,但是中国概率统计教科书中鲜见估算的习题。显然,中国习题没有很好地体现其理念。

“推理”因素。中美两国习题均不强调多步骤推理。这与前面“运算”因素分析中所得的两国都非常忽视符号运算的结果是一致的。其中,美国不仅不重视多步骤推理,也不重视推理,这与美国忽视“运算”水平的结果也一致。中国习题则重视“1步推理”及“无推理”,这与我国重视基本技能与基本运算的传统有关。尽管中国比美国更加重视推理,但是中国强调的推理中缺少猜想。猜想在数学发展史上有不可磨灭的作用。波利亚说:“数学知识首先是被猜想,然后是被证明”[5]。猜想是一种积极的创造性思维活动,它是根据已有的材料和知识做出符合一定经验与事实的推测想象的思维方法。尽管中美两国课程标准都强调需要培养学生的数学猜想能力,但是中国教科书在习题设置上没有很好地体现这种理念。

“知识含量”因素。中美两国的习题基本不包含“3个知识点”以上的知识。其中,美国非常重视单个知识点,中国则非常重视单个及 2个知识点。尽管中国的习题包含更多的知识点,倾向于将数学知识尽可能地综合,但却忽略了现实情境。而美国习题所表现出的概率统计教育的真正目的不在于使学生掌握知识点,而在于学会选择自己熟悉的、实用的方法来处理实际问题,学会自己选择、自己做出合理判断的思考方式。习题中不能仅仅将相关的知识点罗列起来,更应该尝试让学生既能全面掌握知识,又能在不同的情境中选择合理适用的方法来解决问题。

(二)建议

根据上述研究结果,对中国初中统计与概率教科书习题编写方面提出以下建议。

1.淡化计算,深入理解数学知识

虽然中国的标准要求在统计与概率知识方面要淡化计算,但是通过比较我们发现,中国教科书依然强调了计算。必要的计算能力固然重要,但是纯粹的计算不能使学生真正地掌握知识,因此本文建议在教科书编写中淡化无意义的计算,将必要的计算与深入理解数学知识相结合。

2.创设合理情境,引导学生建构

丰富的现实情境可以激发学生的探究兴趣,合理的数学情境能够促进学生数学知识的建构。因此,中国教科书习题需要创设能够激发学生发现问题,解决问题,符合学生现实的探究情境,减少人为创设的痕迹。同时,挖掘有意义的习题提问方式,引导学生进行自主探究,达到真正的自主建构。

3.加强估算与猜想,促进数学化过程

尽管,中国课程标准明确提出要培养学生的估算能力和猜想,但是教科书习题设置中没有明显地体现出来。培养学生的估算能力符合社会发展趋势,在现实生活中有广泛的应用。合理的猜想活跃学生思维,能够创造新的知识,促进横向数学化的发展。培养和发展学生的估算与猜想能力,首先需要有充足、合理的习题,再需要有效解决这些问题的途径。因此,教科书中的习题配备是首要的。

4.活用知识,自主创造

发展学生的解决问题能力是数学教学的目标之一。使学生掌握全面的知识固然重要,但是更重要的是指导学生在现实情境中灵活地运用知识。再创造的最高层次是学生自己的成果中不仅包含解决问题的解法的再创造,而且包括问题的再创造。因此,我们不仅应该强调学生综合运用知识能力,同时也应该发展学生在不同现实情境中活学活用知识的能力。

[1]Romberg T A.Mathematics in Context[M].Madison,W is.:Encyclopaedia Britannica Educational Corp, 1998.

[2]鲍建生.中英初中数学课程综合难度的比较研究[M].南宁:广西教育出版社,2009:15.

[3]中华人民共和国教育部.全日制义务教育数学课程标准 (实验稿)[S].北京:北京师范大学出版社,2001.

[4]全美数学教师理事会.美国学校数学教育的原则和标准[M].蔡金法,等,译.北京:人民教育出版社, 2004.

[5]波利亚.怎样解题——数学思维的新方法[M].涂泓,冯承天,译.上海:上海科技教育出版社,2007.

A Comparative Study on Textbook Problems between Chi nese and American Statistic and Probability Textbooks

J IN Meiyue1,J IA Ping2,ZHANG Xinxin1
(1.Mathematics College,LiaoningNormalUniversity,Dalian 116029,China; 2.Dalian No.3 High School,Dalian 116033,China)

The papermakes a horizontal comparison between the textbooks of PEP and Mathematics in contextmainly at statistic and probability from the aspectof textbook problems.Differences appear in all of five elements:inquiry,context,calculation,reasoning and knowledge containing. On the basis of the comparison and analysis,four suggestions are proposed for later textbook compiling.

juniormiddle school textbooks;statistic and probability;textbook problems;Chinese and US

G633.6

A

1671-6574(2010)03-0001-08

2010-04-08

金美月(1968-),女,朝鲜族,黑龙江佳木斯人,辽宁师范大学数学学院副教授,教育学博士;贾萍(1982-),女,辽宁大连人,大连市第三中学中学一级教师,教育学硕士;张馨心(1983-),女,辽宁辽阳人,辽宁师范大学数学学院课程与教学论专业 2009级教育硕士研究生。