艾滋病疗法的评价及疗效的预测

方 圆,陈灵君,尉敏炜,李宏亮,杨 瑜

(浙江外国语学院理工学院,浙江杭州 310012)

艾滋病疗法的评价及疗效的预测

方 圆,陈灵君,尉敏炜,李宏亮,杨 瑜＊

(浙江外国语学院理工学院,浙江杭州 310012)

对美国艾滋病医疗试验机构ACTG公布的两组数据进行分析,建立了对艾滋病疗法的评价及疗效的模型,对各方案的治疗效果作出了预测与评价,确定了最佳治疗终止时间.

艾滋病;数学模型;随机误差;回归模型

1 引 言

艾滋病的医学全名为“获得性免疫缺损综合症”(Acquired I mmune Deficiency Syndrome, A I DS),它是由“人体免疫缺损病毒”(Human I mmunodeficiency Virus,H I V)引起的.这种病毒破坏人的免疫系统,使人体丧失抵抗各种疾病的能力,从而严重危害人的生命.人类免疫系统的 CD4细胞在抵御 H I V的入侵中起着重要作用,当 CD4被 H I V感染而裂解时,其数量会急剧减少,H I V将迅速增加,导致A I DS发作.

艾滋病治疗的目的,是尽量减少人体内 H I V的数量,同时产生更多的 CD4,至少要有效地降低 CD4减少的速度,以提高人体免疫能力.

根据美国艾滋病医疗试验机构ACTG公布的两组数据[1]:ACTG320是同时服用 zidovudine(齐多夫定),lamivudine(拉美夫定)和 indinavir(茚地那韦)3种药物的 300多名病人每隔几周测试的 CD4和 H I V的浓度(每毫升血液里的数量).193A是将 1300多名病人随机地分为 4组,每组按下述 4种疗法中的一种服药,大约每隔 8周测试的 CD4浓度 (这组数据缺 H I V浓度,它的测试成本很高)。4种疗法的日用药分别为:600mg zidovudine或 400mg didanosine(去羟基苷),这两种药按月轮换使用;600 mg zidovudine加2.25 mg zalcitabine(扎西他滨);600 mg zidovudine加 400 mg didanosine;600 mg zidovudine加 400 mg didanosine,再加 400 mg nevirapine (奈韦拉平).

本文要解决的问题:

(1)利用ACTG320中的数据,预测继续治疗的效果,或者确定最佳治疗终止时间 (继续治疗指在测试终止后继续服药,如果认为继续服药效果不好,则可选择提前终止治疗).

(2)利用 193A中的数据,评价 4种疗法的优劣(仅以 CD4为标准),并对较优的疗法预测继续治疗的效果,或者确定最佳治疗终止时间.

(3)艾滋病药品的主要供给商对不发达国家提供的药品价格如下:600mg zidovudine 1.60美元,400mg didanosine 0.85美元,2.25 mg zalcitabine 1.85美元,400 mg nevirapine 1.20美元.如果病人需要考虑 4种疗法的费用,对(2)中的评价和预测(或者提前终止)有什么改变.

2 模型假设和符号说明

2.1 模型假设

(1)在测试过程中不考虑患者有死亡现象.

(2)不考虑A I DS疗法对人体的副作用.

(3)除所给的两组数据,不考虑其他因素对 CD4的影响.

2.2 符号说明

A表示疗法;A1表示日用药:600mg zidovudine或 400mg didanosine(去羟基苷),这两种药按月轮换使用的疗法;A2表示日用药:600mg zidovudine加 2.25mg zalcitabine(扎西他滨)的疗法;A3表示日用药:600mg zidovudine加 400mg didanosine的疗法;A4表示日用药:600mg zidovudine加 400mg didanosine,再加 400mg nevirapine(奈韦拉平)的疗法;B表示年龄段;B1表示 18至 30岁的年龄段;B2表示 30至 45岁的年龄段;B3表示 45至 60岁的年龄段;C表示CD4的值;F表示因数均方与误差均方的比;P表示等于一个服从 F分布的随机变量的取值大于 F比的概率.

3 模型的建立与求解

3.1 问题 (1)的求解

我们将ACTG320中的被测试者按照 CD4的初始值分为三组:艾滋病前期、中期和晚期.然后我们建立 CD4值与时间,H I V值与时间的二次数学回归模型[2].

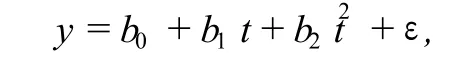
式中的 t称为回归变量,单位为周;b0,b1,b2称为回归系数;影响 y(CD4值或 H I V值)值的其它因素都归为随机误差ε.下面分三种情况进行讨论.

3.1.1 艾滋病前期

艾滋病前期 (CD4的浓度≥200个/μL)共有 439人.根据附件 1中的数据[1],通过MATLB编程[3]得到 CD4值与时间的二次数学回归模型

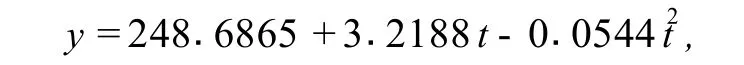
其中,各回归系数的区间估计值分别为 (229.3651,268.0080),(0.9019,5.5358)和(-0.1056,-0.0032),并得到 P值为 0.0000.

另外,我们得到 H I V值与时间的二次数学回归模型

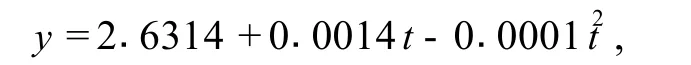
其中,各回归系数的区间估计值分别为 (2.3850,2.8777),(-0.0314,0.0341)和 (-0.0009, 0.0006),并得到 P值为 0.5306.

由图 1-1和 1-2知,患者服用药物之后 CD4值随时间逐渐上升,大约在 30周后其值会逐渐下降;而 H I V值基本上呈下降状态.因此我们建议患者应在 30周左右停止服药.

3.1.2 艾滋病中期

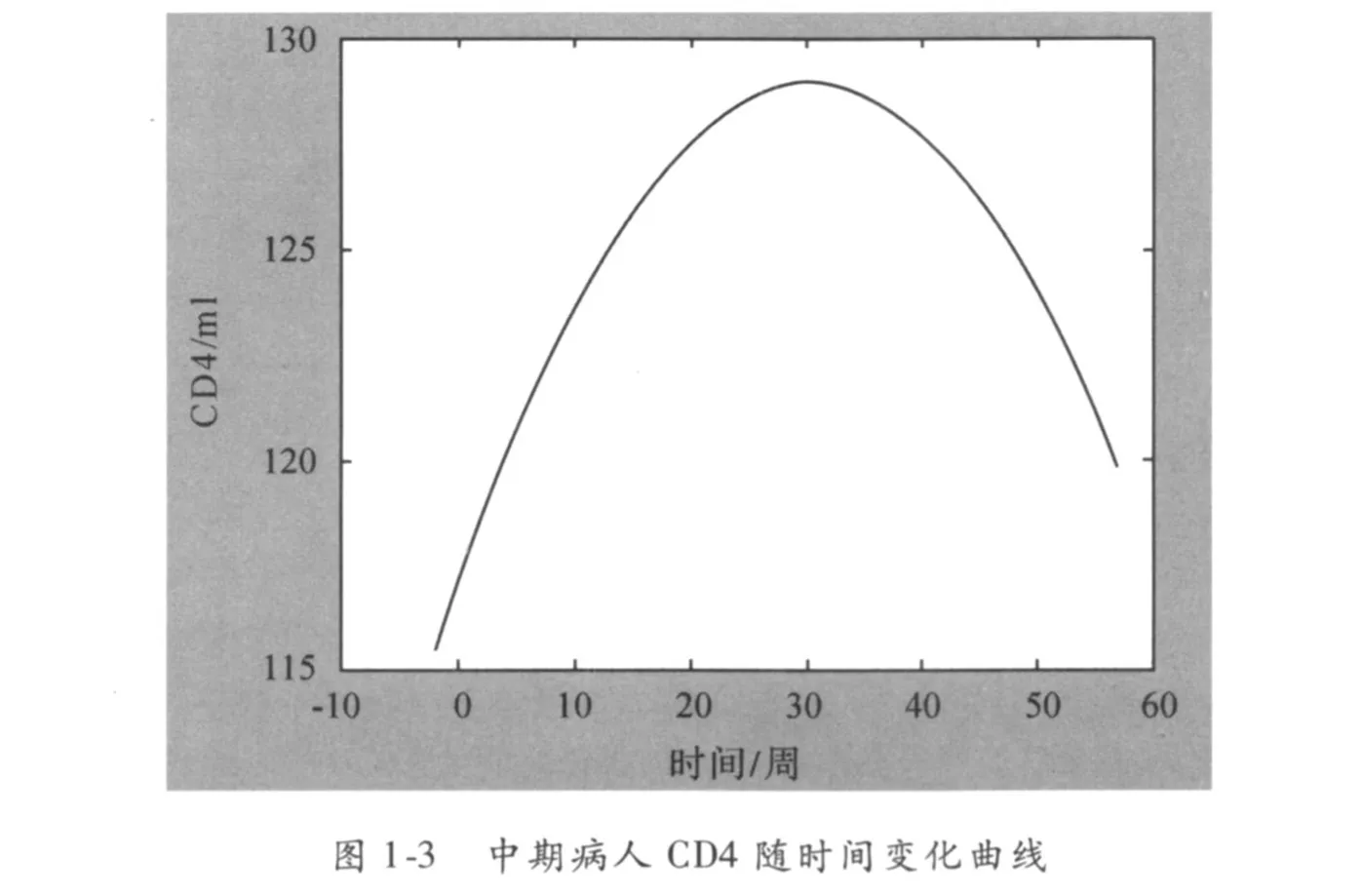
艾滋病中期(50个/μL≤CD4的浓度 ＜200个/μL)共有 876人.根据附件 1[1]中的数据,通过MATLB编程得到CD4值与时间的二次数学回归模型

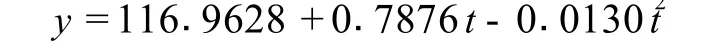
其中,各回归系数的区间估计值分别为 (112.3008,121.6247),(0.0996,1.4756)和(-0.0292,0.0033),并得到 P值为 0.0000.

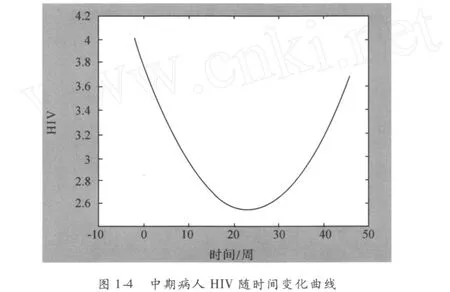
另外,我们得到 H I V值与时间的二次数学回归模型

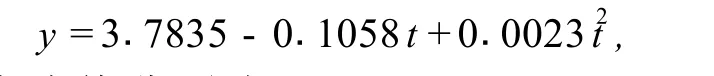
其中,各回归系数的区间估计值分别为 (3.6299,3.9370),(-0.1317,-0.0799)和(0.0016,0.0029),并得到 P值为 0.0000.

由图 1-3和 1-4知,患者服用药物后 CD4值在前 30周呈逐渐上升的状态,但 30周后以较快的速度下降;而 H I V值在前 25周直线下降,随后便逐渐上升.因此,我们建议患者应在 25周左右停止服药,并建议经常测试 CD4值和 H I V值,以便确定新的疗法.

3.1.3 艾滋病晚期

艾滋病晚期(CD4的浓度 ＜50个/μL)共有 350人.根据附件 1中的数据,通过MATLB编程得到 CD4值与时间的二次数学回归模型

其中,各回归系数的区间估计值分别为 (18.9651,23.2198),(-0.1090,0.6677)和(-0.0212,-0.0023),并得到 P值为 0.0007.

另外,我们得到 H I V值与时间的二次数学回归模型

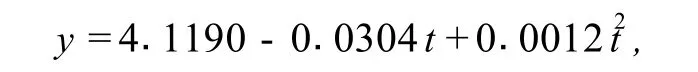
其中,各回归系数的区间估计值分别为 (3.8731,4.3648),(-0.0864,0.0257)和(-0.0004,0.0028),并得到 P值为 0.1846.

由图 1-5和 1-6知,患者服用药物后 CD4值在前 15周缓慢上升,而后呈逐渐下降的状态;而 H I V值在前 15周呈现直线下降状态,随后逐渐上升.因此我们建议患者应在 15周左右停止服药,并建议经常测试 CD4值和 H I V值,以便确定新的疗法.

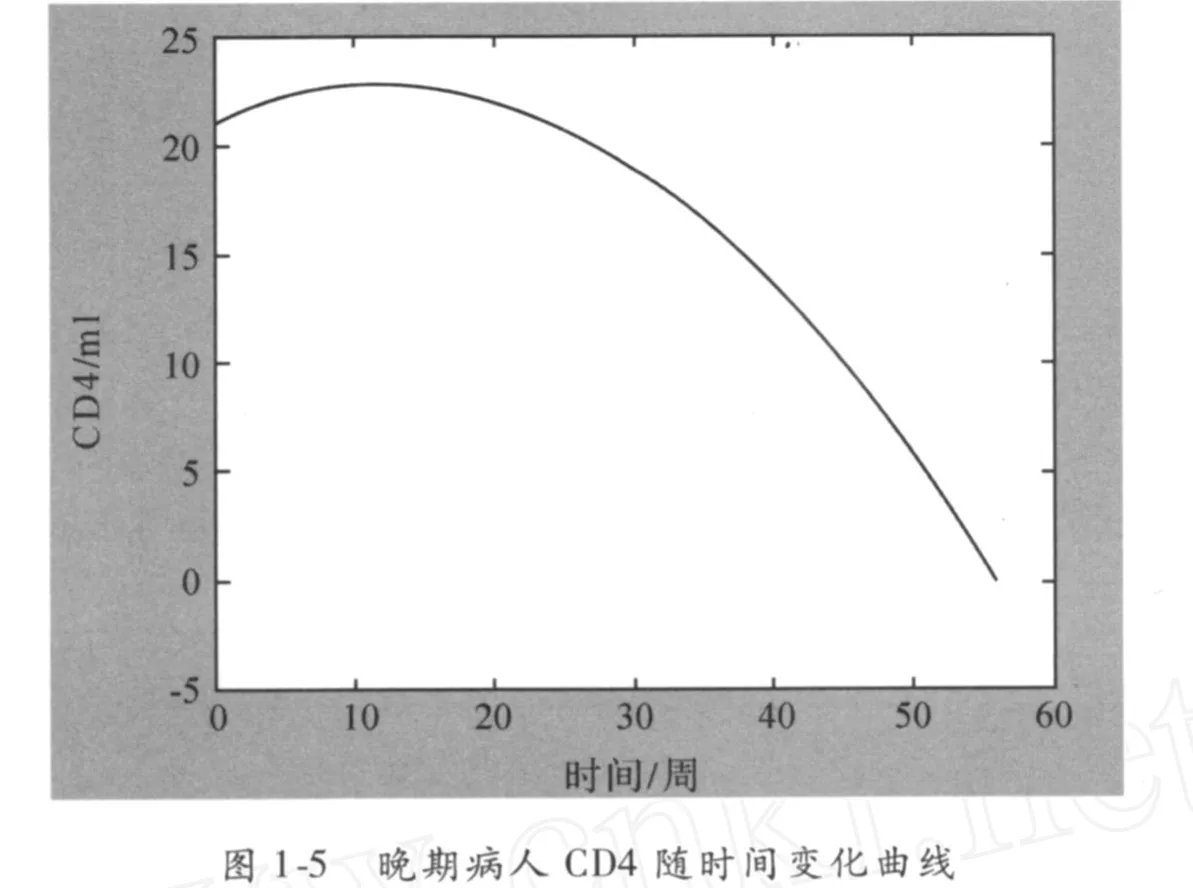
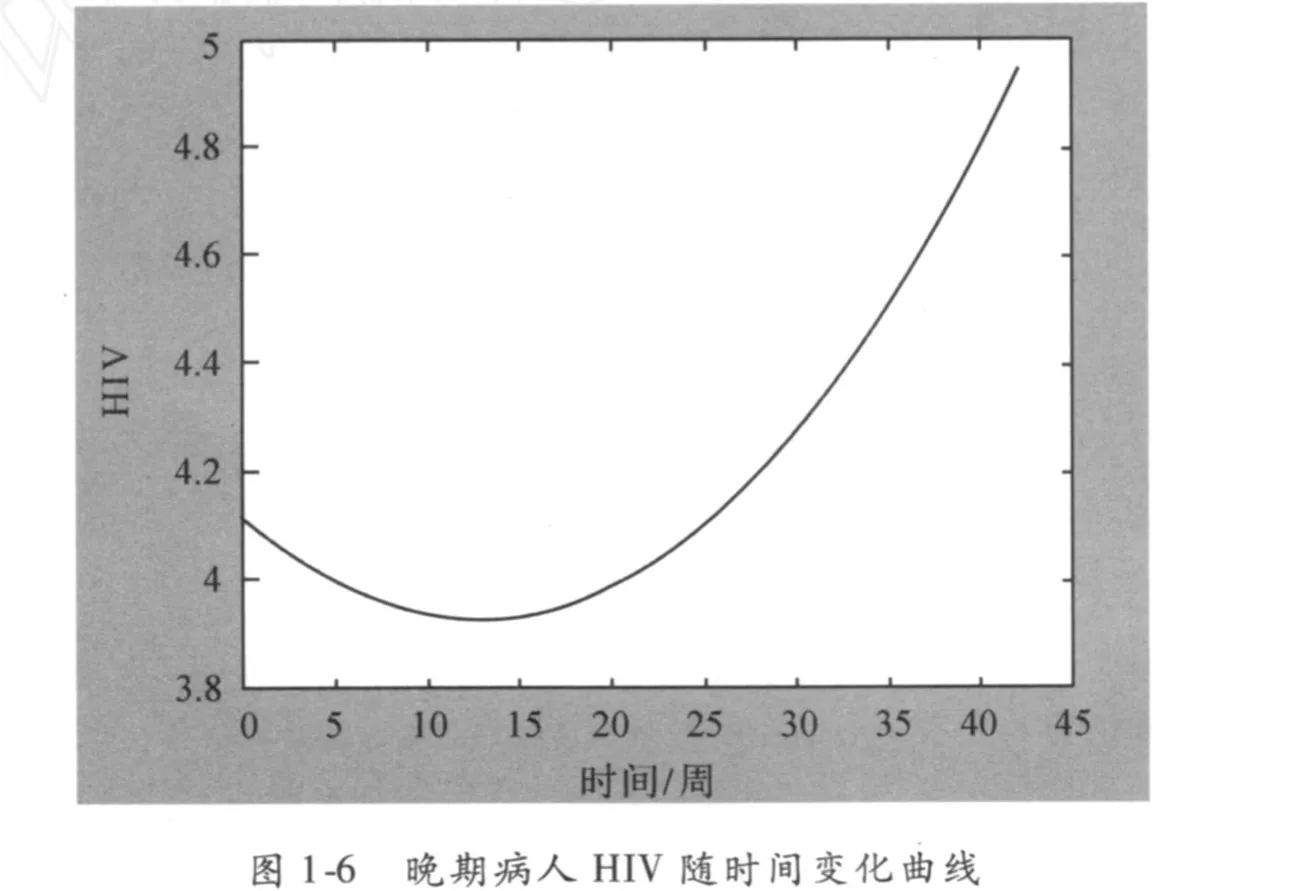
综上所述,对大多数患者来说,该药物在前期还是有比较好的疗效,但到一定时间以后药物的疗效逐渐下降,这时患者应该停止服药.

3.2 问题(2)的求解

我们将 193A中的被测试者按照年龄的不同分为 5组:18岁以下、28～30岁、30～45、45～60和 60岁以上.根据所给的数据,我们进行了筛选,将只进行了两次以下测试的数据或不符合生活实际的数据(如 I D为 13的患者,log(C+1)三次测试都为 0).由于 18岁以下与 60岁以上的数据相对缺乏,在此我们不予考虑.

结论 1 4种疗法从优到劣分别为 A4,A3,A2,A1.事实上,log(C+1)与 CD4成正比关系,即当 CD4增大时,log(C+1)也增大.因此我们只须考虑 log(C+1)的变化速率即可.

我们分别考虑不同的疗法.在A1疗法中,我们计算出每组中不同人的 log(C+1)值的变化速率(负值代表减少),再用求平均值法计算出该组总的 log(C+1)值的变化速率,即得到了不同年龄段对 log(C+1)值的变化的影响.

同理,我们可以得到接受A2,A3,A4三种疗法的不同年龄段对 log(C+1)值的变化的影响.

通过计算,我们得到数据见表 1.

表 1 不同疗法和不同年龄段的 log(C+1)的变化速率

由表 1可知,只有A4疗法的 log(C+1)值是增加的,即 CD4是增加的.这说明 A4疗法不仅有效地降低了CD4的减少速度,而且产生了更多的CD4,这对控制病情是最有利的.而A1,A2,A3三种疗法的CD4值是减少的,通过对数据的比较,我们得出CD4值的减少速率是A3＜A2＜A1,即这三种疗法从优到劣依次是A3、A2、A1.因此这四种疗法的从优到劣分别为 A4,A3,A2,A1.

结论 2 疗法对 log(C+1)的变化速率有较显著的影响,而年龄对 log(C+1)的变化速率的影响很小,可以不予考虑.

事实上,假设患者的年龄和疗法对 log(C+1)的变化速率都可能有影响.因此我们利用双因素试验的方差分析进行讨论.设因数A为疗法,B为年龄段.由于疗法与年龄段的每一组水平组合 (Aj,Bj)进行一次试验得到的值χij(不同年龄段 log(C+1)的变化速率)相互独立 (i= 1,2,3,4;j=1,2,3,4),因此不考虑两因数间的交互作用,得到表 2.

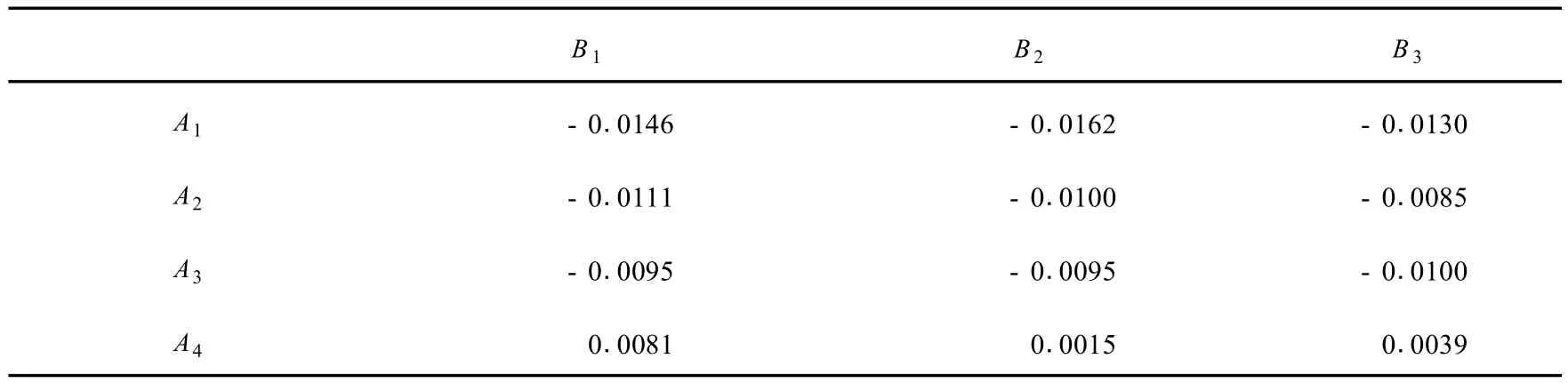
表 2 双因素方差分析的数据结构

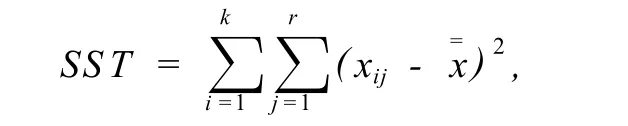
利用无交互作用的双因素方差分析的计算公式

其中,SST是总误差平方和;xij(i=1,2,…,k;j=1,2,…,r)是由行因素的 k个水平和列因素的r个水平所组合成的 k×r个总体中抽取的样本容量为 1的独立随机样本;=x 是全部 kr个样本数据的总平均值.在MATLAB中进行无重复试验的双因素方差分析中得到数据见表 3.

表 3 双因素方差分析表

根据 P值说明疗法对 log(C+1)的变化速率有较显著的影响,而年龄对 log(C+1)的变化速率的影响很小,可以不予考虑.

结论 3 接受最优疗法A4的最佳治疗终止时间为 17.9592周.

事实上,由结论 2知,我们只考虑时间对 CD4值的影响,不考虑年龄对 CD4值的影响.

根据附件 2中的数据[1],通过MATLB计算我们得到 log(C+1)值随时间的变化曲线,见图 2.从图中我们可以看出,随时间的变化,log(C+1)值先上升后下降,也就是说 CD4值也是先增多后减少,并且在第 17.9592周达到最大值.因此最佳治疗终止时间为达到最优疗效的时间应为第 17.9592周.

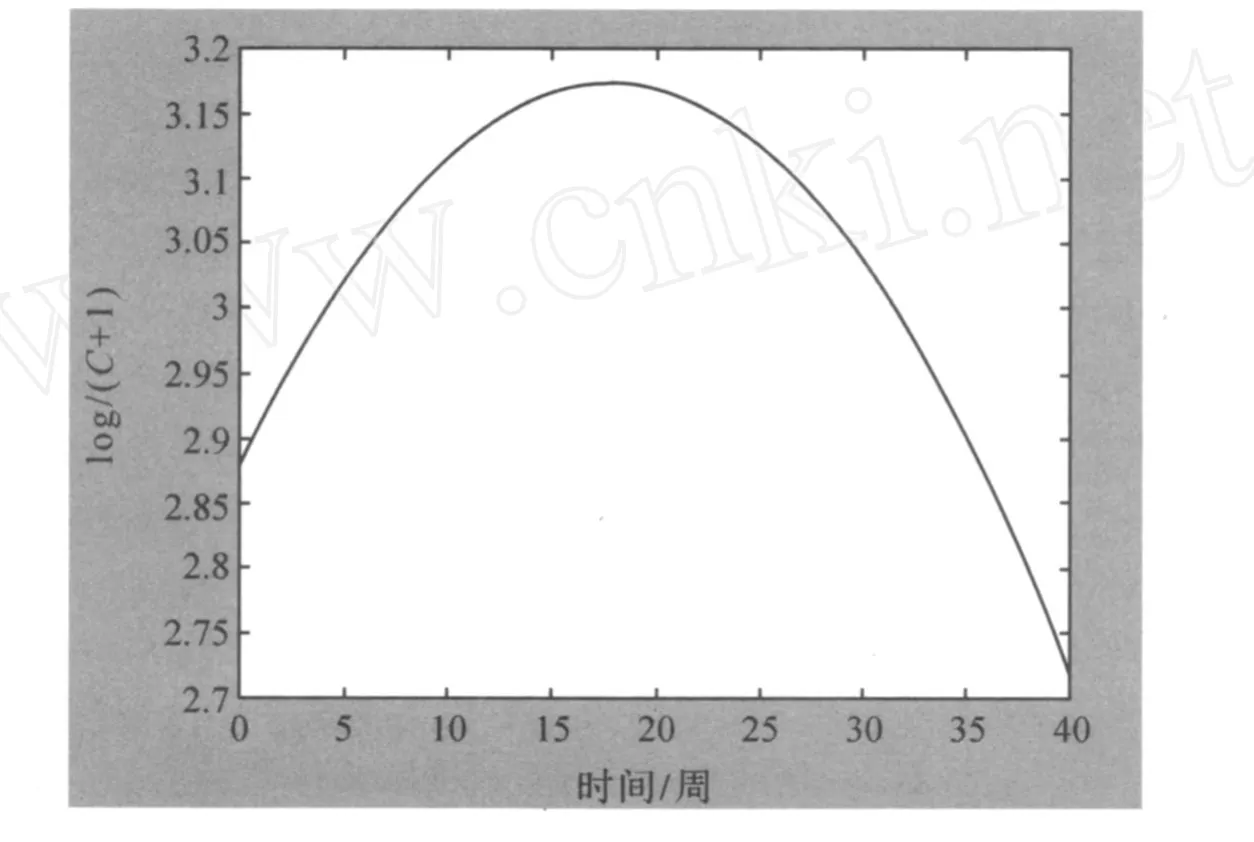
图 2 log(C+1)随时间变化曲线

3.3 问题(3)的求解

根据问题 (2)的解答,我们已经知道这四种疗法从优到劣依次是 A4,A3,A2,A1.下面我们以A4疗法为例,考虑

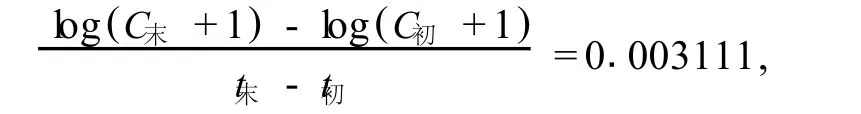
上式可转化为

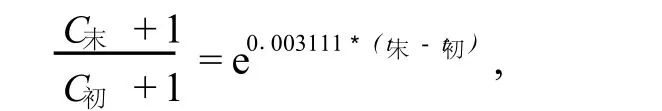
而 t末-t初的值一般小于 50,故 e0.003111＊(t末-t初)大于 1但无限的接近 1.由此可得 C末“＞”C初,但两者无限地接近.同理,在 A3,A2,A1疗法中有 C末＜C初,但两者无限地接近.又根据四种疗法的优劣,若我们假设某人初始状态的CD4值为 C初,那么选择A4疗法时,C末大于C初但无限地接近,而选择其他三种疗法时 C末小于 C初但也都是无限地接近,A3疗法的 C末比 A2疗法的C末更接近 C初,A2疗法的 C末又比 A1疗法的 C末更接近 C初.由以上讨论知,这四种疗法对CD4值的影响不同,但这其中的差距是相当小的.因此我们将费用作为主要影响因素来考虑对疗法的选择,而将疗效的差异作为次要影响因素来考虑对疗法的选择.

根据题中所给的药品价格,我们求得不同疗法的日均费用分别为 A4(3.65美元),A3(2.45美元),A2(3.45美元),A1(1.225美元).由上可得,A1疗法的价格低廉,但疗效相对不够理想.如果经济能力有限但需要治疗,可以考虑采用.A2疗法价格高而疗效也不是最理想的,因此不推荐采用;A3疗法价格适中疗效又相对平稳,长期使用可以使 CD4浓度保持较稳定状态,非常有利于控制病情;A4疗法价格昂贵见效快,但长期使用疗效与 A3疗法差不多,考虑到不发达国家患者的经济情况,因此不推荐使用.综上考虑,我们推荐采用A3疗法进行长期治疗.

4 结 论

本文针对文献[1]提出的问题,建立了艾滋病疗法的评价及疗效预测的数学模型.

(1)利用二次数学回归模型,对附件 1[1]中的数据进行了统计分析,得到药物在前期对大多数患者还是有比较好的疗效,但到一定时间以后药物的疗效逐渐下降,这时患者应该停止服药.

(2)利用双因素方差分析,得到A4为最优疗法并且最佳治疗终止时间为 17.9592周. (3)在问题 (2)的基础上分析得到A3疗法比较适合进行长期治疗.

本文是在“2006年全国大学生数学建模竞赛”参赛文章(获浙江赛区二等奖)的基础上,通过参考命题者提供的解答要点,进行修改整理而得.

[1]全国大学生数学建模竞赛组委会.2006高教社杯全国大学生数学建模竞赛 B题[EB/OL].[2006-09-15].http://mcm.edu.cn/mcm06/Problems2006c.asp.

[2]贾俊平.统计学[M].2版.北京:清华大学出版社,2006.

[3]薛定宇,陈阳泉.高等应用数学问题的MATLAB求解 [M].北京:清华大学出版社,2004.

The Therapy Evaluation and Efficacy Prediction of AIDS

FANG Yuan,CHEN Lingjun,WEIMinwei,L IHongliang,YANG Yu
(School of Science and Technology,Zhejiang International StudiesUniversity,Hangzhou 310012,China)

By analyzing two data sets announced by the United Statesmedical experimental institute ACTG,this paper establishes the model of therapy evaluation and efficacy,makes a prediction and evaluation of treatment effect of each scheme,and determines the best end time of treatment.

A I DS;mathematicalmodel;stochastic error;regression model

O212.1;O211.9

A

1671-6574(2010)03-0066-08

2010-03-29

方圆(1985-),女,浙江兰溪人,浙江教育学院理工学院数学与应用数学专业 2004级本科生;陈灵君 (1987 -),女,浙江永康人,浙江教育学院理工学院数学与应用数学专业 2004级本科生;尉敏炜(1985-),男,浙江绍兴人,浙江教育学院理工学院数学与应用数学专业 2004级本科生;李宏亮 (1973-),男,浙江淳安人,浙江外国语学院理工学院数学系讲师,理学博士.

＊通讯作者:杨瑜 (1981-),男,浙江安吉人,浙江外国语学院理工学院数学系讲师,理学博士.