中学生运用一般化与特殊化策略解决数学问题的研究

隋文静,鲍建生

(华东师范大学理工学院,上海 200241)

中学生运用一般化与特殊化策略解决数学问题的研究

隋文静,鲍建生

(华东师范大学理工学院,上海 200241)

在数学认知水平评价体系中,一般化与特殊化是第四层次探究性理解水平的一个重要指标。对上海市某重点初中六至八年级的测试表明,所测试各年级的学生在一般化与特殊化策略与思维上的总体表现较低;特殊化策略及思维的运用好于一般化;低年级学生多运用特殊化的策略,一般化思维运用普遍较差,但随着年级的增加有所提高;特殊化与一般化思维的灵活运用上存在一定思维定势。

一般化;特殊化;数学认知水平

“青浦实验的新世纪行动”的大样本调查(上海市教育科研青浦实验研究所,2007)形成了数学认知水平的评价体系,将数学认知水平划分为操作性记忆水平、概念性记忆水平、说明性理解水平和探究性理解水平四个层次[1]。后经研究又形成了各级认知水平的二级指标。其中,第四层次探究性理解水平的二级指标包括:发现并形成合适的数学问题、解决非常规的和开放性的数学问题、提出猜想与构造模型、特殊化与一般化以及数学推理与证明五个方面[2]。

为了了解学生在解决较高认知水平的数学问题时,在这五个方面的具体表现,我们设计了数学认知水平调查测试卷,在上海市某重点初中进行测试,本文仅分析测试结果的一个方面,即特殊化和一般化的策略及思维情况。二级指标中的特殊化与一般化,是指全面结合已分解的各要素及其关系,按照模型需要对已有的数学概念、程序、性质和命题进行推广或特殊化。比如画图帮助思考;在不能直接解决的情况下计算特殊情况;或从一般情况入手,把问题作为一般化的一个特例来看待等等。

一、研究过程

(一)研究对象

本研究选择上海市某重点初中的六、七、八年级全部学生作为测试对象,发放测试卷 597份,回收 597份,其中六、七、八年级分别为 194人、199人和 204人。

(二)研究方法

采用测试卷调查法及试题分析法。对三个年级的全部学生进行数学认知水平调查测试,然后对涉及特殊化与一般化策略与思维的测试题目进行试题分析。具体分析学生在一般化与特殊化思维方面表现如何,使用哪些一般化和特殊化的策略,在证明一般化结论时表现如何。将各年级测试卷所得数据用 SPSS13.0进行统计。

(三)测试工具

为三个年级分别编制一套数学认知水平测试题,题目需要较高认知水平,考察学生在发现提出问题、开放性题目、提出猜想、一般化与特殊化、推理证明等方面的能力。试题来源主要是:(1)青浦实验所采用的测试卷题目;(2)参考多方面研究并根据被调查学校的教学进度改编而成。

每个年级有 6道测试题,年级之间有相同的题目,以期对年级之间做一些比较。测试卷中涉及一般化与特殊化策略及思维的题目是“钟面问题”“式的规律及证明”“数的规律及证明”和“填数字问题”。三个年级的测试题详细情况见表 1。

表 1 各年级试题情况统计

二、测试结果与分析

(一)总体表现

将涉及一般化与特殊化测试题的各年级的总得分转化成得分率 (用小数表示),统计情况见表 2。从表 2可见,涉及一般化与特殊化的题目三个年级的平均得分率都不到 0.5,三个年级的最高得分率分别为 0.97、0.89、1.00,但七、八年级的最低得分率都是 0,六年级最低得分率只有 0.06。可见在涉及一般化与特殊化的题目上表现不佳。

表 2 各年级总得分率统计

(二)“式的规律及证明”分析

该题目给出一组式的模式,要求寻找规律并证明规律。学生需要综合考虑给出的 4个式子的特征及联系,用字母代替数字,得出一般规律,并完成证明,这是对一般化思维以及对猜想与证明的认识的考察。题目如下:

观察下列等式,你能发现什么规律?试用一个数学等式表示这个规律并证明。

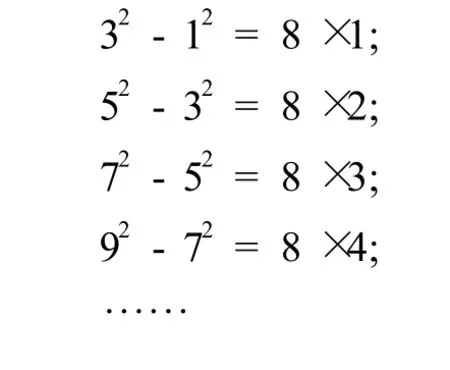
1.得分率统计

结果表明,该题目七、八两个年级的总得分率差不多,为 0.27左右。“寻找规律”平均得分率为 0.4387,而“证明规律”只有 0.1056。两个年级在每个小题上的表现也差不多。可见,涉及一般化的题目对学生来说难度很大,尤其是证明规律得分率相当低(详见表 3)。

表 3 “式的规律及证明”得分率统计

2.作答情况分析

一是“寻找规律”方面。

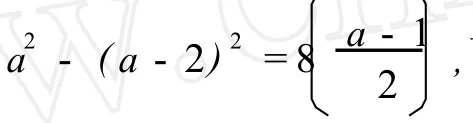
以上各种回答情况反映了学生一般化策略使用上达到的层次。(5)、(6)两种回答均是使用了一个变量正确表达所给模式的规律,并对变量的取值有严密的考虑,达到了一般化的水平;(2)、(4)的回答也正确反映了所给模式的规律,但未完全达到一般化水平,因为(2)的解答对变量没有限制条件,而(4)的解答包含两个变量,忽视了变量的制约关系,这两种解答都“扩大”了原有模式的规律;(3)的解答描述的规律往往只适合第一个表达式,没有正确描述一组模式的规律,没有达到一般化水平;而文字表述所达到的一般化程度不同,有描述局部特征也有一般化的描述。

七、八两个年级学生的作答情况见图 1(横轴数字 (1)至 (7)分别对应上述七种作答情况)。可见,八年级在“寻找规律”上“忽视变量的条件限制”和“包含两个变量”的情况明显比七年级多,而七年级未作答的情况明显比八年级多。可见,虽然两个年级在“寻找规律”上的得分率都很低,但八年级学生却比七年级学生更“接近一般化”,他们更多地发现了模式的共同之处,只是由于忽视了变量的条件和限制,最终没能达到一般化。而七年级学生的低得分率主要由于未作答。

二是“证明规律”方面。

在“证明规律”方面,主要的作答情况有 5种:(1)验证一个特殊值;(2)验证多个特殊值; (3)将等式两边同时化简,得到 8n=8n的形式,完成证明;(4)证明完全正确(用代数语言形式化的证明);(5)未作答。

分析各种证明方法的一般化的水平发现,(1)、(2)的证明都利用特殊性的例子来说明一般性结论,是“类属性”的证明,而不是一般性水平的证明;(3)的证明是基于代数形式化的证明,但证明的“格式”不对,它对等号两边的代数式同时化简最后得到 8n=8n。究其理解的心理学根源,可能是在一般化的代数思维中,把等号理解为一种显示相等的关系结构,一种状态:相等,等价,同类或平衡[3]158,所以证明过程就是在保持这一平衡的关系。而证明时对等号的理解除了是平衡的关系外,更应当是从左可化到右,从右可化到左的过程化的理解;(4)的证明是形式化的一般化证明,且一般化中对等号的理解也是恰当的。

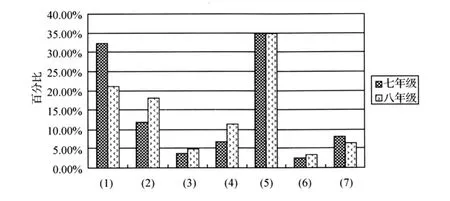
图 1 “寻找规律”作答分析

学生的作答情况按年级分布如图 2所示 (横轴数字 (1)至 (5)分别对应上述五种作答情况)。可见,“证明规律”方面,两个年级的主要错误都是“未证明或规律错误”,即大多数学生在前一问没有找到规律或没有作答。七年级“验证一个特殊值成立即完成证明”的情况明显多于八年级。而八年级“8n=8n”的证明以及完全正确的证明均明显多于七年级。可见七年级学生证明了特殊、具体事实的成立即会承认一般化结论的正确性,而八年级学生更倾向于给出形式化证明,尽管形式化证明过程中有逻辑错误。

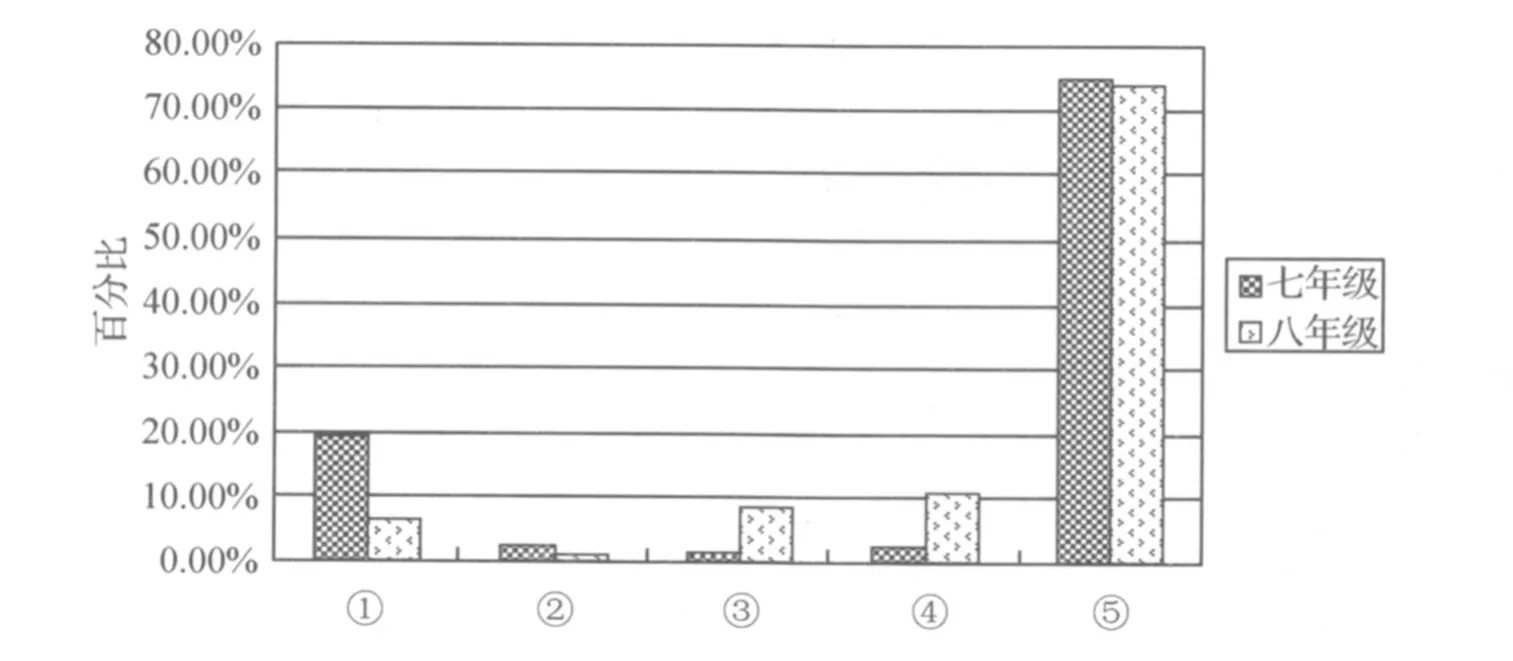
图 2 “证明规律”作答分析

(三)“数的规律及证明”分析

该问题是对任意三位数互换个位与百位数字后做差的结果的规律探索。要求学生理解文字叙述的意义后给出具体的例子,通过特殊化的方法寻找到一个结果,再在一般化水平上证明这个结果。该题目考察借助特殊化方法探索,并给出一般化结论并证明的能力,题目如下:

写下一个三位数,使得这个三位数的百位、十位、个位是连续的自然数,再把它的百位和个位的数字换一个位置得到另一个三位数,然后从较大的三位数中减去较小的三位数。(1)求所得的差,(2)证明这一结果。

1.得分率统计

该题目按年级的得分率见表 4。总体上,该题两个年级的得分率相差很大,八年级为0.5176,而六年级只有 0.1873。在“举例”方面的得分率明显高于“证明”。八年级在“举例”、“证明”的得分率都明显高于六年级。八年级“举例”的得分率接近 0.7,而六年级只有 0.4左右,六年级在“证明”的得分率只有 0.0902,而八年级有 0.4283。可见,八年级学生基本可以将问题特殊化,一般化的证明有困难;而六年级学生在特殊化方面及一般化证明方面均有明显困难。

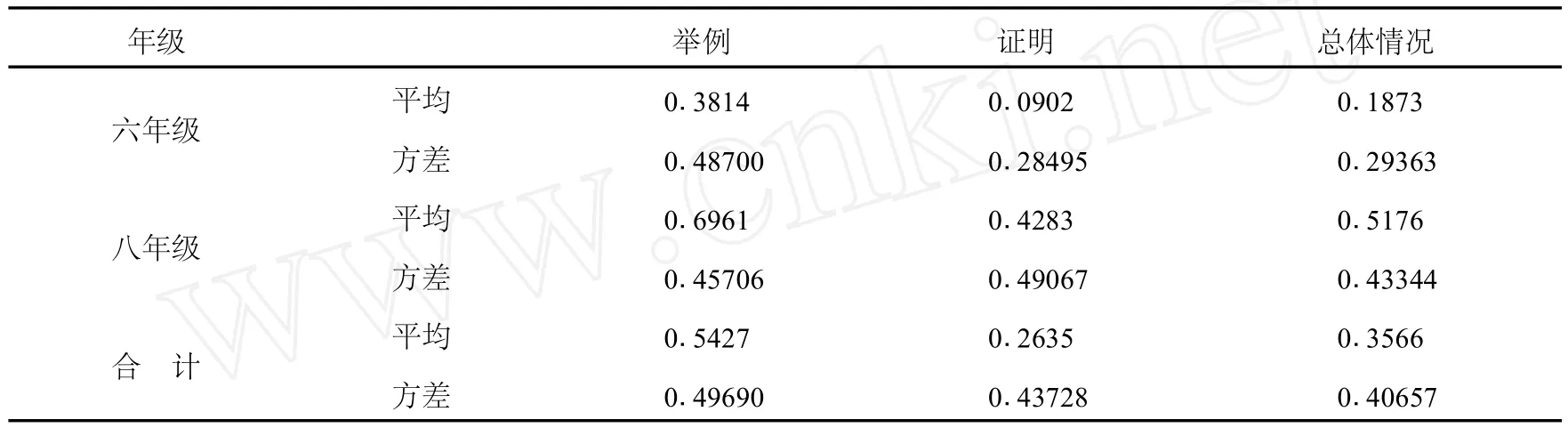
表 4 “数的规律及证明”得分率统计

2.作答情况分析

在一般化的证明中,学生使用的证明方法大致有 6种:(1)枚举法证明:枚举所有情况并一一验证;(2)代数的证明:基于代数语言的形式化证明;(3)位值的证明:例如因为十位数是不变的,而百位大数比小数大 100,个位大数比小数小 2,所以 200-2=198;(4)举特例成立即得到证明;(5)分析竖式减法的过程得到证明。如个位需借一位,得到结果的末位比 10小 2,为 8,十位被借走一位且两数相等,需再借一位,即结果十位数比 10小 1,为 9,百位被借走一位,且减数比被减数大 2,结果百位数为 2-1=1;(6)未作答或其它。

在各种证明方法中,枚举法、代数的、位值的、分析竖式减法的证明都是具有一般化水平的证明,证明依据的是所有符合题意的特殊例子的共同、普遍规律。尽管枚举法依赖具体的例子,但由于考虑了所有情况,也具有一般性;位值的、分析竖式减法的证明依赖算数过程,是算数层面一般化,是用具体数字、式子表达一般化的思想;而代数的证明则是基于符号表征,用形式化的语言表达一般化。严格说,只有代数证明才是真正意义上的一般化。而举特例的证明只能算作实例水平上的证明,是“类属性”的证明,而不是一般性水平的证明,但“类属性”证明方法比较易于理解,又不失一定的严格性,值得作为引向形式化证明的铺垫[3]138。

各种证明方法的学生按年级分布见图 3(横轴数字 (1)至 (6)分别对应上述六种作答情况)。可见,在一般化证明中,六年级近 80%的学生未作答,远远高于八年级。八年级有近40%学生采用代数的证明,而六年级最多采用的是举出特例成立的证明方法。代数的证明不到 5%。位值、分析竖式的证明两个年级差不多,但只占很少比例。有趣的是,八年级没有一例枚举法的证明,猜测这可能由于八年级学生形式化证明的思维定势影响。总体看,八年级学生一般化的形式化的证明是明显好于六年级的,六年级形式化的一般化层面的证明很少,大多是基于特例的证明。

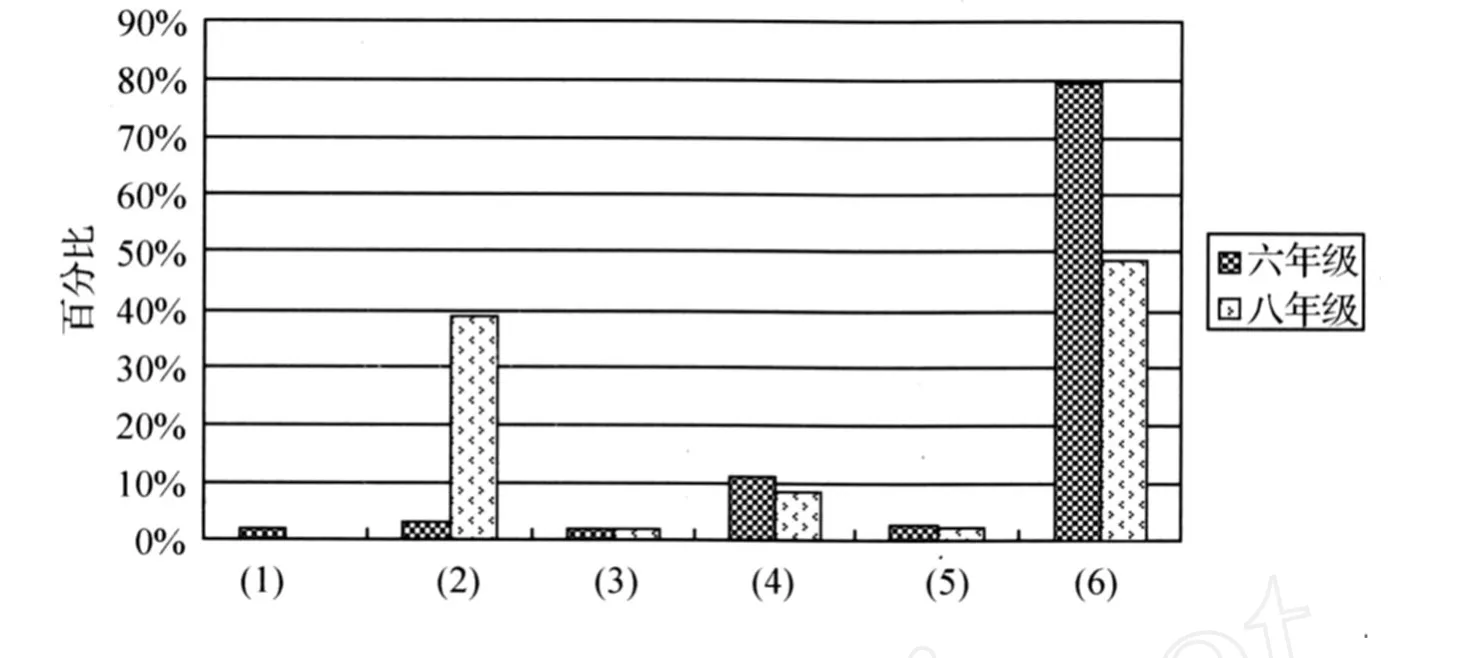
图 3 “一般化证明”作答分析

(四)“钟面问题”和“填数字问题”的分析结果

“钟面问题”是六年级与八年级共有的题目,这是一道在国内已有许多实验与研究的经典开放题,它的全部答案共 124个,具有一个“好”的开放题的许多特点:非常规,参与性与趣味性,探索性等。这道题目的解决需要特殊化与一般化策略的有效运用,第一问需要学生使用特殊化的策略,凑出结果为 0的算式,第二问则需要在凑数、尝试中发现一般性的规律,将特殊的方法推广到一般化层面,找出更一般的策略。具体题目如下:

挂钟的钟面上有 12个数字:1,2,3,…,11,12.要在这 12个数字中间添上加号“+”或者减号“-”,得到一个算式,使得这个算式的结果为 0.

(1)这道题目共有一百多种不同的解答,写出你想到的 4种不同的解答;

(2)你有什么方法可以找到更多的解答?

“填数字”问题是六、七年级共有题目。要求学生在圆圈内填入适当的数,使每条边上两个圆圈中的数之和等于方框内的数。这两个问题都可以通过设未知数,列出三元一次及四元一次方程组得以解决。第一问填三个数字,此时三元一次方程组有唯一解,因此答案唯一,所以用一般化思维(列方程组)容易解决,用特殊化方法 (代入数字尝试)不易解决;第二问是填入四个数字,但此时的四元一次方程组有无穷多解,因此用特殊化的方法,代入数字尝试更易解决。具体题目如下:

在图 4和 5中的圆圈内填入适当的数 (可以是负数),使每条边上两个圆圈中的数之和等于方框内的数。

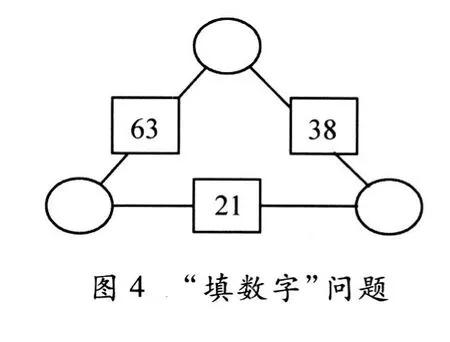
由于篇幅有限,这里仅简述“钟面”和“填数字”问题的测试结果。

“钟面问题”中,八年级在寻找特殊化方法方面明显好于六年级,但两个年级在将特殊化方法推广到一般化策略时表现都不好。八年级学生在提出一般化、可推广的策略方面优于六年级学生,六年级学生毫无策略的凑数、非数学的回答较八年级多。“填数字问题”中,一般化求解的方法对六年级学生来说难于特殊化求解方法。六年级有 42%的学生能灵活地转换于一般化与特殊化的方法之间,七年级的这一比例明显更多,为 64%。而不能灵活转换的学生当中,两个年级的学生都是只掌握特殊化方法的学生比例较高,而只掌握一般化方法的学生比例较低。

三、讨论

以下讨论中,我们将六、七年级划入低年级组,八年级作为高年级组。综上所述,测试各年级学生在一般化与特殊化策略与思维上的总体表现较低,由于题目背景、难度的不同,学生在一般化与特殊化方面的表现不尽相同,但总体上,测试显示以下几点结果:

(一)特殊化策略的运用好于一般化

测试学生的特殊化策略题目的得分率都高于一般化策略的题目。大部分学生能够有效使用特殊化策略,如考虑特殊情况、代入具体数字等,而且高年级表现更好。即使较难的开放题(钟面问题),学生也能尝试从特殊情况入手,给出一些具体回答。但将具体问题推广到一般情况或一般化证明的题目得分率都很低。

这一现象与特殊化与一般化思维的本质有关,特殊化思维考虑的是具体、固定的对象,直观简单;而一般化思维考虑的是概括、可变的对象,在将固定数学对象换成可变数学对象的一般化过程中需要综合考虑已分解的各要素及其关系、变量间的互相关系、变量的限制条件等问题,所以一般化往往难于特殊化。

(二)低年级学生较多运用特殊化的策略

调查发现,低年级学生趋向于用特殊化的策略,他们更多用语言表达规律,借助直观理解,遇到难以理解的问题首先想到举例子。调查中,低年级学生在钟面问题中大多采用凑数尝试的方法,一般化、可推广的策略明显少于高年级学生。低年级学生对一般化的证明大多数是未作答的,即使存在少数的证明,也多是将证明转化为枚举所有特例,一一证明其成立或验证一个或多个特例的方式。而研究中的高年级学生没有人想到用枚举法证明一般化,他们努力想给出一个形式化的证明,虽然大多数证明也失败了。

按皮亚杰的儿童智力发展理论,初中低年级学生认知水平处于具体运算阶段,在很大程度上要借助具体对象进行思维操作,所以更趋向用特殊化策略;而随年级升高学生认知水平逐渐进入形式运算阶段,能够不受具体对象限制,在抽象、概括水平上进行思考。

(三)一般化策略运用普遍较差,但随着年级的增加有所提高

从调查结果看,涉及一般化思维及证明的“式的规律及证明”问题得分率最低,该题目中学生可以发现规律,续写后面的式子,但就是无法上升到一般化层面用符号语言代替具体数字。其它涉及一般化策略及证明的表现也都很差,似乎一旦出现变量 n,得分率就会“垂直下降”。但随着年级的升高,一般化思维的运用也有所提高,高年级学生形式化的证明明显好于低年级学生。

究其原因,除了以上提到的认知水平的差异外,六、七年级学生处于由算数思维向代数思维过渡的阶段,这本身也是由特殊化思维向一般化思维的过渡,对于字母、变量的含义理解不全面,这可能导致一般化运用策略过程的困难。但需要注意的是,高年级一般化过程、形式化的证明的层次也不高,得分率未超过 0.5,甚至出现形式化证明 0.1左右的得分率。

(四)特殊化与一般化策略的灵活运用上存在一定思维定势

有意思的是,在“填数字”问题中,第一小问采用特殊化的方法是很难快速凑对答案的,而第二小问采用特殊化方法能立即获得解答,而采用一般化方程的办法就没那么直观。结果显示,六年级有 5.2%只做对第一问,七年级有 8%只做对第一问,这部分比例七年级略高,虽然都没超过 10%,但也说明一个有趣的问题,部分学生或许列方程“埋头苦算”,却忽视了带具体数字尝试一下的办法,跳不出形式化的“束缚”,而随年级升高学生的这一“束缚”变得明显。

在“数的规律及证明”问题中,六年级学生用枚举法证明,这是从特殊化的角度考虑,但由于题目背景特殊,用枚举法可以穷尽所有情况,因此枚举法证明不失为一种好方法。而八年级学生没有一人用枚举法,似乎想努力寻找形式化的证明,即使证明是错误的。其原因可能是,随年级升高,学生在接受了较多形式化证明及一般化策略后,形成一定思维定势,以致于想不到使用直观而容易的特殊化方法,但由于本研究侧重对学生的测试,其具体原因还有待进一步研究。

[1]贺真真.关于教学目标因素分析的数据报告——以上海市青浦区数学学科为例[J].教育发展研究,2007 (7-8A):78-83.

[2]周超.八年级学生数学认知水平的检测与相关分析[D].上海:华东师范大学,2009.

[3]李士锜.PME数学教育心理[M].上海:华东师范大学出版社,2001.

Survey on M iddle School Students’Strategies of Generalization and Speci alization i n Mathematics Problem Solvi ng

SU IWenjing,BAO Jiansheng
(School of Science and Technology,East China No rmalUniversity,Shanghai 200241,China)

In the assessment framework ofmathematical cognition level,generalization and specialization are among the key indicators of the highestmathematical cognition levels.This survey on three grades in a key middle school in Shanghai has some initial findings.Firstly,the students’overall performance in strategies of generalization and specialization is not good.Secondly,the use of strategies and thought of specialization is better than generalization.Thirdly,low grade students are more likely to use strategiesof specialization than to use strategiesof generalization,but the situation is changed along with passing grades.Finally,there are some thinking patterns that affect students’using of strategy of generalization and specialization.

generalization;specialization;mathematical cognition level

G633.6

A

1671-6574(2010)03-0022-08

2010-04-01

隋文静(1985-),女,新疆克拉玛依人,华东师范大学理工学院数学系课程与教学论专业 2008级硕士研究生;鲍建生(1960-),男,浙江金华人,华东师范大学理工学院数学系教授,博士生导师。