深圳地铁重叠隧道列车振动响应测试与数值分析

凌 昊 郑余朝 仇文革 龚 伦

(西南交通大学土木工程学院,610031,成都∥第一作者,博士生)

0 前言

国内外学者对地铁列车振动引起的环境问题进行了许多研究,其中最重要也是最直观的的方法是现场振动测试。如：1977年德国柏林州与1982年英国伦敦地铁都进行过振动测试研究。在国内,1988年和1990年潘昌实、谢正光曾在北京地铁区间隧道内进行过列车振动测试与相应的动态有限元分析研究[1-2]。文献[1-5]均是在现场测试的基础上,利用频谱分析方法,得出地铁列车振动引起的轨道振动加速度的数定表达式;再根据车辆系统振动简化模型,建立了模拟轮系的运动方程,从而推导出地铁列车振动荷载;并根据这个振动荷载进行相应的数值计算,从而得到了相关的数据和结论。

在面对像深圳地铁一期工程中出现的重叠隧道这种复杂结构时,更需关注列车振动导致的结构动力特性。文献[3]曾根据上海地铁某区间隧道现场实测的振动加速度数据,对上海轨道交通4号线南浦大桥站至塘桥站区间工程中的近距离交叠隧道,在列车振动荷载作用下的动力响应进行了有限元数值模拟,并得到了一些有指导意义的结论。该交叠隧道工程与本工程相比,虽然在线形变化上存在一定相似之处,但在地质情况、结构形式和施工方法上均存在较大差异,因此不能简单套用相关分析和结论。

在振动研究中,比较理想的是对所有振动项目,如加速度、速度和动应力等进行全面的现场实测。然而这对于运营中的地铁隧道,需要耗费较大的时间和精力,也涉及相关的安全问题,为客观条件所限制。因此,在本次研究中仍然采用了以往惯用的研究方法,即：对测得的加速度进行数定,得到了地铁列车的振动荷载,并进行了有限元数值计算。本文在对重叠隧道所有典型断面的数值分析中,均根据相应断面处实测的加速度时程来计算相应的振动荷载。

1 工程概况

在深圳地铁一期工程的规划设计中,由于受沿线建(构)筑物的限制,在我国地铁修建史上第一次出现了区间隧道左右线上下重叠、交错的结构型式。工程集中在罗湖站——大剧院站的三个区间。

罗湖站——国贸站区间,左右线隧道从水平并行的两个单洞隧道逐步过渡到上下重叠的单洞双层区间隧道;国贸站——老街站区间,为上下线重叠的单洞双层隧道结构;老街站——大剧院站区间,从上下线重叠的单洞双层结构过渡到水平并行的两个单洞分离结构。

2 列车振动影响的现场测试

对结构受振动影响的衡量指标通常采用振动速度、加速度、动应变等物理量。本次主要对竖向振动加速度进行了测试。

测试采用目前较先进的DH5923动态信号测试仪。DH5923动态信号测试分析系统包含动态信号测试所需的信号调理器(应变、振动等调理器)、直流电压放大器、抗混滤波器、A/D转换器、缓冲存储器,以及采样控制和计算机通信的全部硬件,并配有操作方便的控制软件和分析软件。

2.1 振动监测的断面和测点布置

2.1.1 监测断面布置

本次列车振动测试,主要是为了考察结构在列车振动荷载作用下的工作状态,故选择了有代表性的隧道4种断面形式进行振动监测(见图1)。

图1中,CK1+700断面位于国贸站——老街站区间的线路半径为350 m的曲线段上,为矿山法单洞双层单隔板结构。该断面处隧道主要在全风化层中通过。其余3个测试断面均位于老街——大剧院站区间,也为矿山法暗挖复合结构。其中CK2+330断面为单洞双层双隔板结构,CK2+390和CK2+435断面都为单洞分离结构,分别呈上下并行或交错布置,隧道主要在中-微风化层中通过。

2.1.2 测点布置

每个监测断面均布置4个竖向加速度测点。测点分别布置在上、下层隧道的钢轨和道床面板上。其中钢轨上的测点可监测列车通过时动荷载直接作用在轨道上所产生的加速度,道床面板上的测点可监测到已受钢轨、连接部件等减振后作用在隧道结构上的振动加速度。

2.2 监测数据的分析

隧道各断面测点的加速度值见表1,测试得到的典型加速度时程如图2。

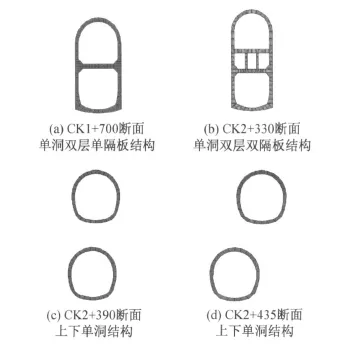
图1 测试断面的隧道结构

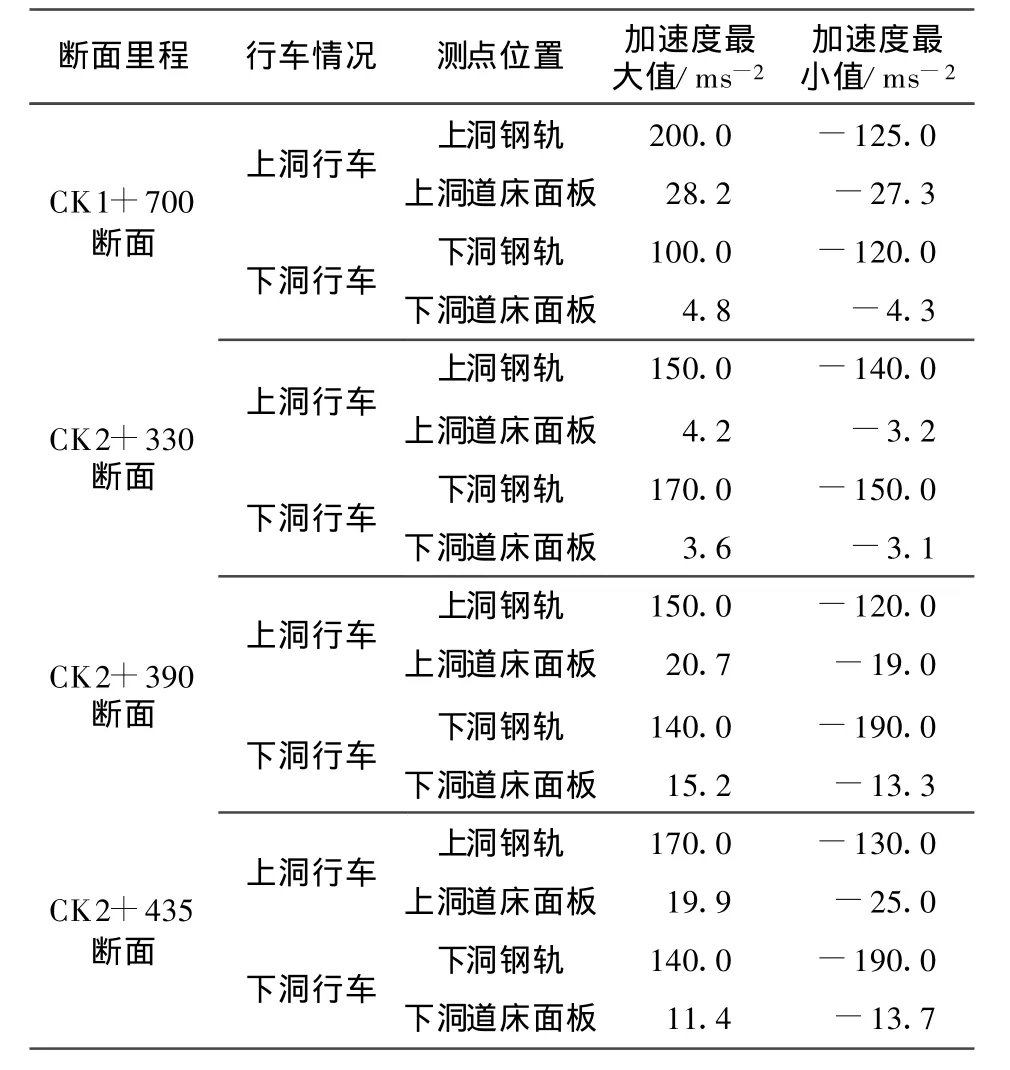
表1 各测点最大加速度

图2 CK1+770断面上洞行车时上洞钢轨竖向加速度

分析现场振动测试得到的钢轨和道床面板上加速度的时程曲线表明：钢轨上的加速度较大,其最大值约200 m/s2;至道床面板上时,加速度衰减明显,其最大值为24 m/s2。各断面的钢轨加速度差异不大,且无明显的规律可循,受线形、钢轨平顺度、运行速度等综合控制。

3 列车振动的数值计算

计算中只进行平面数值模拟分析。整个数值模拟分析分两步进行：第一步,计算在静力场情况下隧道结构的受力;第二步,是在输入静力初应力基础上计算在列车振动荷载作用下隧道的结构受力。

3.1 静力计算

静力计算主要采用大型有限元程序ANSYS,通过单元生死和应力释放来进行。

1)计算模型的范围：上边界取至地表,左、右及下边界均取至隧道开挖轮廓线外30 m。

2)边界条件：上表面为自由面,左、右边界为水平约束,下边界为竖向约束。

3)计算步骤：初始平衡——开挖——支护——二次衬砌(由单元的生死和应力释放来逐步实现)。

4)计算参数：地层、结构材料的参数见表 2所示。

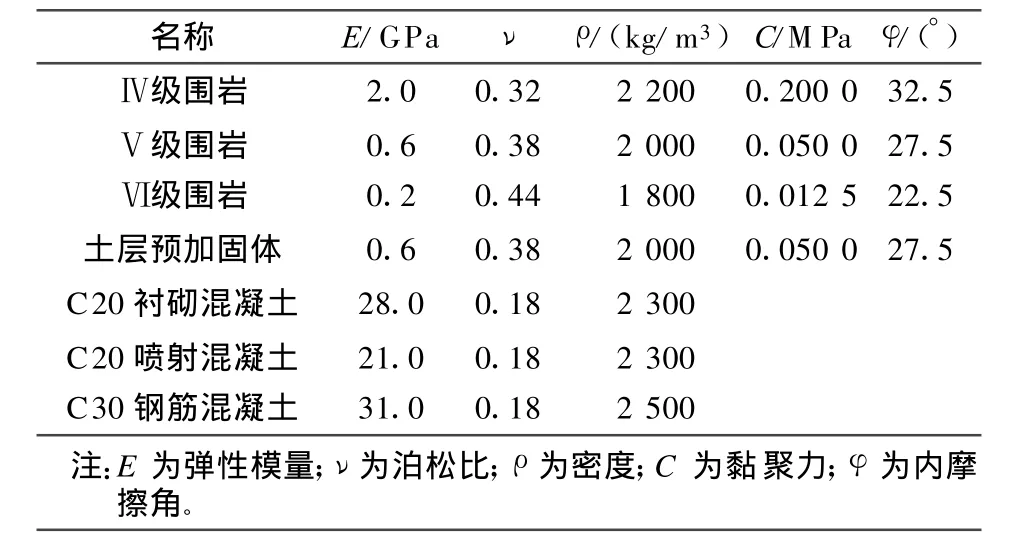
表2 围岩及材料计算参数

3.2 列车振动计算

3.2.1 计算原理

1)整体的动力平衡方程见下式：

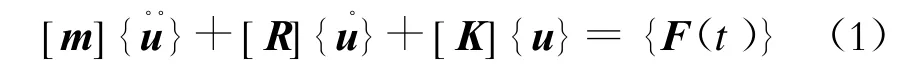
式中：

[m]——质量矩阵;

[R]——阻尼矩阵;

[K]——刚度矩阵;

{F(t)}——节点动荷载向量列阵。

2)积分采用Newmark隐式积分方法,并取其系数 δ=0.5,γ=0.25。

3)阻尼采用通用的瑞利(Rayleigh)阻尼,如式(2)所示：

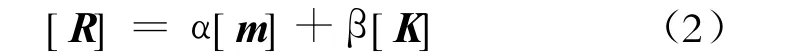
式中系数 α、β可由式(3)、(4)两式联立求解得到。

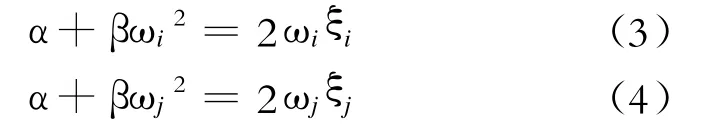
式中：

3.2.2 列车振动荷载

通常,地铁列车车辆的车体重心在纵、横向都是对称的,故可只分析一个转向架的一侧。其竖向振动简化模拟轮系为图3所示的单自由度模型。这个轮系以速度v在不平顺的轨道上行驶,轮轨间相互作用力为P2(t)。模型中的各参数如下：一个车轮的质量m1=1.735×103kg,传递到一个车轮上的车体和转向架的质量m2=10.837×103kg,弹簧系数 k=2 500 kN/m;阻尼系数 c=24.58 kN◦s/m。

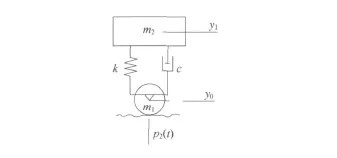
图3 列车竖向振动模型

在图3所示的坐标下,竖向模拟轮系的运动平衡方程为：

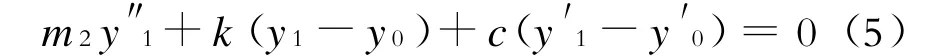
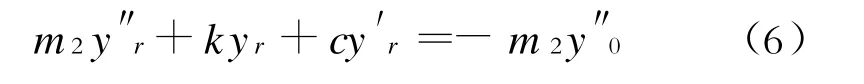
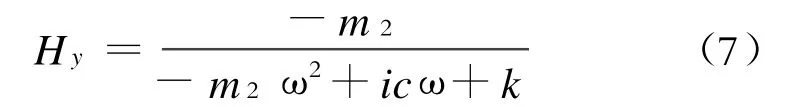
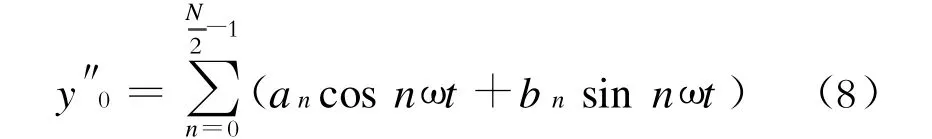
同理可得：

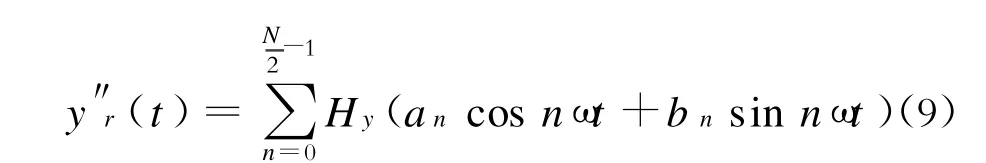
由图3所示的模拟轮系,据达朗贝尔原理可以得到轮轨间的相互作用力为[4]：

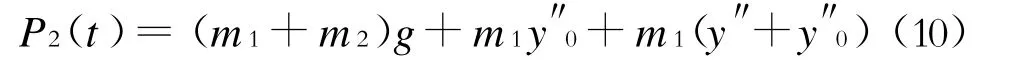
式中：

g——重力加速度。

将其变换为沿轨道均布的线荷载,则CK1+770断面列车振动对隧道的竖向激振荷载P的时程如图4所示。

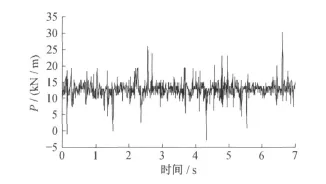
图4 CK1+770断面上洞行车时上洞振动荷载

3.2.3 计算模型

1)有限元模型：在此仅列出CK2+330断面的模型,见图5。

图5 CK2+330断面的动力分析模型

2)边界条件：上边界为自由面,左、右及下边界为人工边界。具体计算方法参见文献[6]。

3)计算工况：根据行车方式不同,共分3个工况,即上洞行车、下洞行车和上下洞同时行车。

3.3 计算结果分析

计算得到的隧道各断面相应的最大速度、加速度和应力值见表3。典型的时程图谱见图6～11。

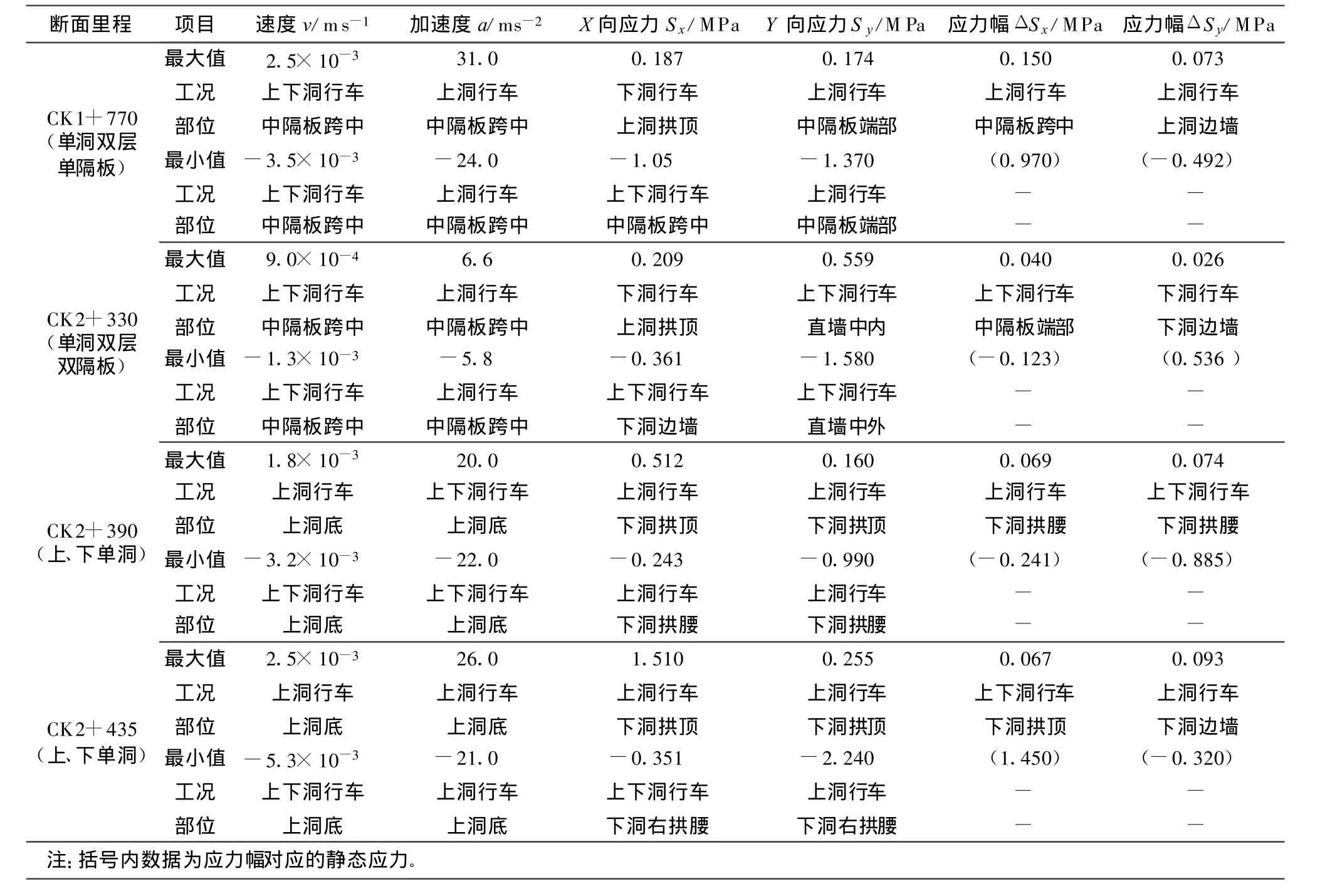
表3 各断面最大、最小振动值统计表

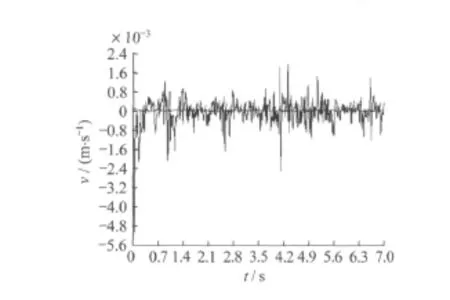
图6 CK2+435断面上洞行车时上洞仰拱底速度

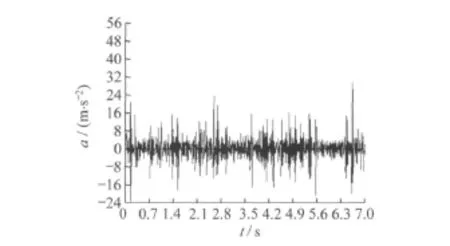
图7 CK1+700断面上洞行车时中隔板中点加速度

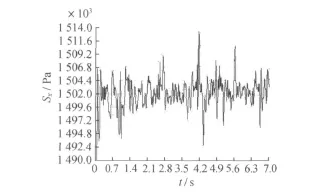
图8 CK2+435断面上洞行车时下洞拱顶X向应力

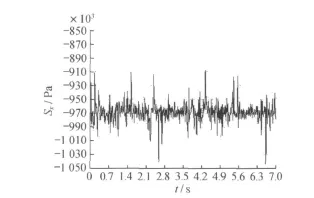
图9 CK1+700断面上洞行车时中隔板中点X向应力

从各指标来看,其相应的最大值为：速度5.3 mm/s;加速度31 m/s2;X向拉应力1.510 MPa,压应力1.050 MPa;Y向拉应力0.559 MPa,压应力2.240 MPa;X向应力幅0.150 MPa;Y向应力幅0.093 MPa。计算所得的道床面板处加速度值与实测值比较,除个别断面外,大多数差值在20%以内,表明计算结果与实际符合较好。

对于单洞双层结构,在振动荷载相差不大的情况下,双隔板的振动反应比单隔板小很多。如：最大速度减小了64%,最大加速度减小了79%,最大X向应力幅减小了73%,最大Y向应力幅减小了64%。

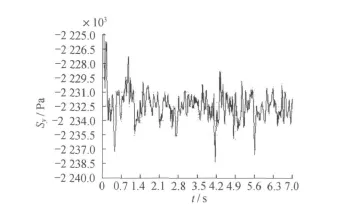
图10 CK2+435断面上洞行车时下洞右拱腰Y向应力

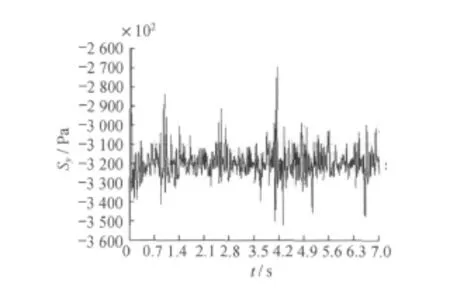
图11 CK2+435断面上洞行车时上洞左拱脚Y向应力

从受力来看,由于围岩的预压作用,最不利位置并不出现在隔板的跨中位置,而是出现在隔板与边墙的连接处或仰拱与边墙的连接处。上、下单洞分离结构的不利位置出现在下洞的拱顶和拱腰处,上洞的列车振动对下洞影响较大,同时由于下洞埋深相对更深,静态应力也更大。

从应力幅与静态应力比较来看,一般在10%以内,个别较大比值也在30%以内,且一般应力幅最大位置与应力最大位置并不同时出现。因此,从总体上看,静载是结构设计的控制荷载,但在设计时需考虑列车动载或冲击荷载的影响。

根据GB 50010—2002《混凝土结构设计规范》相关规定,现对疲劳强度进行验算。

取结构重要性系数为1.1,荷载分项系数统一取1.4。将振动应力合成内力后,对最不利内力进行验算。验算结果均小于结构的允许疲劳强度,满足规范要求。

4 结语

由现场振动测试结果,并结合动力数值分析结果,可得出以下结论：

1)根据现场测试,钢轨上的竖向振动加速度较大,最大值约200 m/s2;隧道结构道床面板上振动加速度最大值为24 m/s2,衰减明显。通过计算值与实测值的比较,两者符合良好。

2)在列车振动荷载作用下,对于单洞双层结构,不利位置在隔板与边墙的连接处或仰拱与边墙的连接处;上、下单洞结构的不利位置出现在下洞的拱顶和拱腰处。经验算,动应力均小于结构的允许疲劳强度,满足规范要求。

3)在列车振动荷载作用下,对于单洞双层结构,双隔板的结构反应小于单隔板结构。

4)对隧道结构而言,静载是结构设计的控制荷载,但在设计时需考虑列车动载的影响。

[1]潘昌实,谢正光.地铁区间隧道列车振动测试与分析[J].土木工程学报,1990(2)：21.

[2]潘昌实,李德武,谢正光.北京地铁列车振动对环境影响的探讨[J].振动与冲击,1995,14(4)：29.

[3]陈卫军,张璞.列车动载作用下交叠隧道动力响应数值模拟[J].岩土力学,2002,23(6)：770.

[4]张玉娥.地铁列车振动对隧道结构激振荷载的模拟[J].振动与冲击,2000,19(3)：68.

[5]刘维宁,夏禾,郭文军.地铁列车振动的环境响应[J].岩石力学与工程学报,1996,15(S1)：586.

[6]高峰,关宝树.隧道地震反应分析中几种边界条件的比较[J].甘肃科学学报,2004,16(1)：109.