半导体环形激光器的非线性分岔动力学研究
张 彬,毛陆虹,谢 生,张世林,郭维廉,陈 燕,于 欣
(天津大学电子信息工程学院,天津 300072)
当前半导体环形激光器作为单片光子集成的应用越来越受到人们的重视,特别是在全光转换和光学双稳态的研究方面[1-2].电学双稳态在实验上已得到证实[3],国内外众多学者就激光器的双模式动力学问题进行了大量的实验和理论研究[4-5].
在半导体环形激光器中,两个相互反向传输的光波通过两种机制相互作用,即光学增益饱和和背散射.前者在文献[5-6]中进行了讨论,指出这种机制可以实现光学模式锁定.背散射效应在文献[3]中作为一种重要的机制被引入双稳态动力学体系中,但作者只求解了几种特殊情况的解,没有从非线性动力学角度进行整体细致的分析,特别是对突变点出现的原因和性质、极限环形态等特性没有进行仔细的理论分析.搞清楚背散射效应参数对系统性能的影响无论从理论角度还是从实验角度都是非常有意义的.
笔者利用了非线性分岔这一现代数学方法对半导体环形激光器进行分析和计算,在分析过程中没有进行任何的数学简化,研究了环形激光器中泵浦参数所引发的霍普夫分岔现象.
1 双模式非线性模型
设器件工作在单模条件下,半导体环形激光器的动力学可以通过下面的一系列微分方程组进行描述.
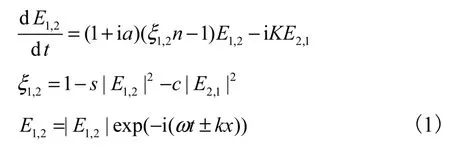
式中1,2E 是相互反向传输的 2个模式的复振幅[3].方程中的相关参数进行了无量纲化处理,各相关物理量数值和意义[5]见表1.
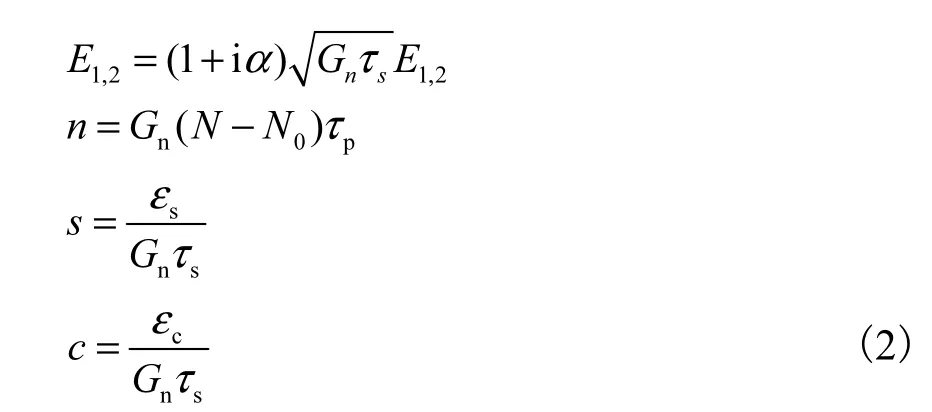
其中n为本文主要讨论的分岔参数泵浦因子,它是载流子密度的归一化表示.式(2)中和光学增益饱和效应相关的参数是归一化自饱和系数 s和交叉饱和系数 c;与背散射效应相关的参数是 K,K为一个复数.为了简化可以将1iα+进一步吸收到1,2E中,忽略其线性部分并用1/c进行归一化处理.对1,2E 微分,取其振幅和相位部分可以将复数微分方程组转化为实数形式,即

表1 相关物理参数的含义和数值Tab.1 Meanings and values of related physical parameters
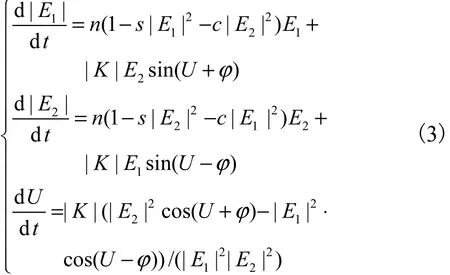
式中 U=U1-U2,U1和 U2分别表示 E1和 E2的相角.如果把泵浦参数 n看作分岔参数,环形激光器的双模竞争问题将转化为一个非线性分岔的问题.
令式(3)左端为零.注意到系统具有平衡点满足方程

可知式(3)组成的非线性系统(以下简称系统)具有平衡点(E1,E2,μ)=(E*,E*,μ),进行坐标平移,即

对式(3)进行泰勒级数展开,得到其一阶线性部分,即 Jacobian矩阵为
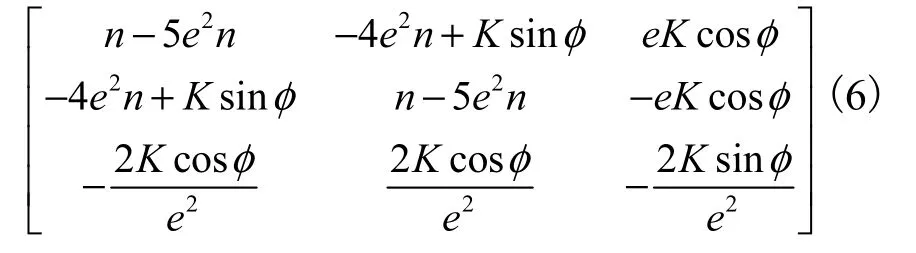
该系统具有3个本征值:
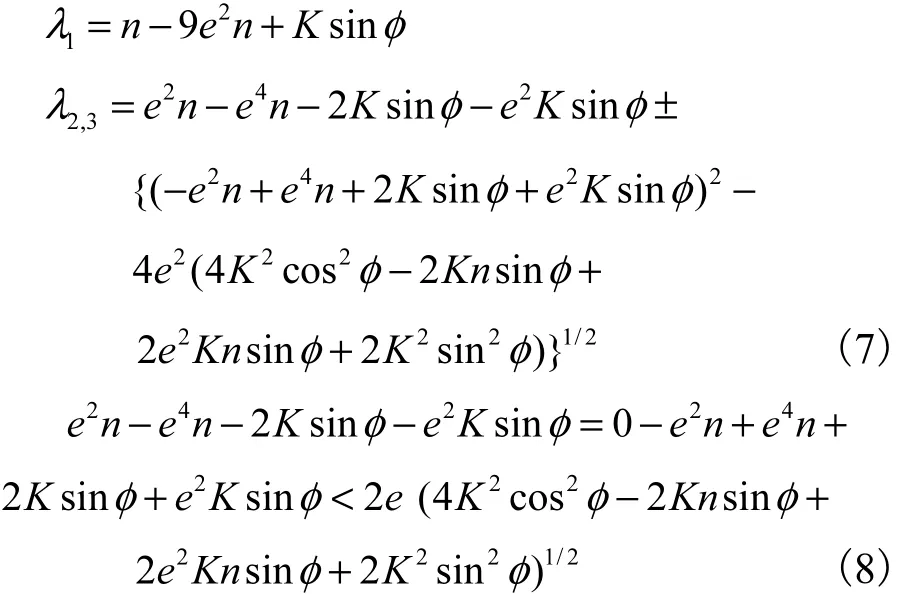
当满足式(8)的条件时,2,3λ的实部为零,系统具有2个纯虚数的根,将会发生霍普夫分岔.
下面将使用非线性数值方法对霍普夫分岔引发的复杂非线性动力学进行进一步的分析.
2 非线性数值分析
为了找到这一微分方程系统的解,使用了现代非线性分岔算法.选择背散射参数为||1K=、0.1ϕ=进行计算.非线性分岔算法的主要步骤是求解系统平衡点曲线,在平衡点曲线上检测奇异点,如果检测到的奇异点将引发极限环则从此极限环点出发计算极限环曲面.非线性分岔算法从几何拓扑角度整体地研究非线性系统,并可视化地展现此系统的拓扑骨架,找到系统发生质变的关键点.
首先是找到系统的平衡点,主要采用牛顿连续性算法,这一算法的主要步骤由下一迭代点的预测、修正和步长控制组成,详细的算法步骤见文献[6].系统的平衡点曲线如图 1所示,点 H为系统的霍普夫分岔点,选择背散射参数为||1K=、0.1ϕ=.
算法的下一步骤是在平衡曲线上检测奇异点,这里主要指霍普夫分岔点的检测,即计算平衡曲线上每个点的本征值,找到其中本征值为虚数的点,图 1中的 H点即表示系统的霍普夫点,在这一点处将发生极限环振荡现象.
根据现代非线性理论,从霍普夫分岔点开始将引发一系列的极限环,因为分岔参数的变化形成特定的曲面.如果系统初始状态处于极限环附近,经过无限长的时间,系统的运动将无限趋近于此极限环运动,从而引发系统的周期性振荡.对于系统y=f(x),极限环是具有特定周期 T的孤立轨线.在此轨线上满足x(0)=x(T),由于 T未知,可以定义处于[1 0]的等效系统,从而列出极限环上满足的方程为
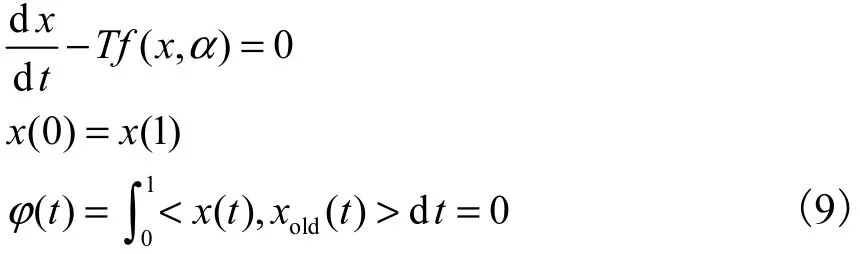
其中 xold是在上一迭代步骤计算得到的解.如果把时间间隔分成 N等份,使用差分代替导数,则式(9)可以转化成
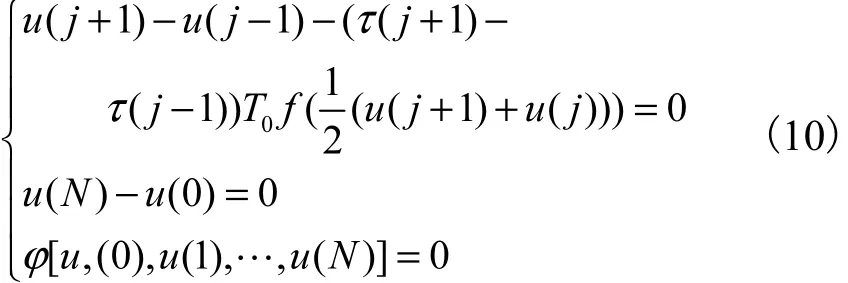
其中 u(j)(j=1,…,N) 代表每一个极限环上离散点的解.使用这一迭代步骤可以计算得到系统的极限环曲面,如图 2所示,选择背散射参数,则为K=1、ϕ =0.1.
通过图 3所示的庞加莱截面可以更清楚地观察到系统的振荡运动.庞加莱截面是截取微分流形的特定截面形成的相平面.图 3是截取不同的泵浦参数 n形成的 E1-E2和 E1-U的二维相平面图.图中可以观察到 E1-E2极限环呈现蝴蝶结形态,因而 E1-E2将形成交替荡振运动.从霍普夫分岔点开始的极限环将随着泵浦参数的增加,逐渐远离原点,其吸引范围将逐渐增加.有趣的是,在泵浦参数增加到一个特定的数值,极限环将趋于某一特定的极限环.超过这一阈值,极限环消失,系统重新恢复为文献[5-6]描述的具有2个稳定的极限点的锁定状态,在分岔理论中称这一阈值为极限环的极限点.从微分几何角度,可以清楚地看到系统发生质变的2个点分别对应于霍普夫分岔点和极限环的极限点.从物理角度看,在霍普夫分岔点处背散射效应将导致系统的振荡运动,在极限环的极限点处光学非线性增益饱和效应将迫使系统进入光学模式锁定状态.这2个突变点将相空间清楚地分为3个部分,分别对应于文献[3]指出的3个区域:双向连续波区(bi-CW)、交替振荡区(bi-AO)和无向锁定区(UNI).
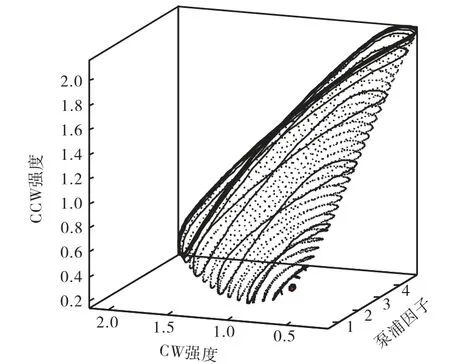
图2 系统的极限环曲面Fig.2 Limit cycle surface of system
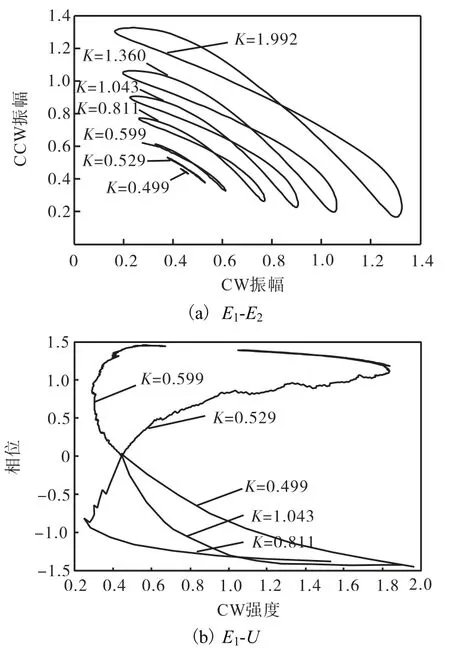
图3 极限环曲面的庞加莱截面Fig.3 Poincare section of limit cycle surface
系统在不同的泵浦参数时的非线性运动表示见图4,其中图4(a)和(b)表示系统处于交替振荡区,极限环已经出现,2个反向传输模式的振幅和相位波呈现交替振荡的特性,三者之间存在相位差π/2,这与文献[3]的描述相一致.图4(a)为刚刚起振的情况,图4(b)为经过一定时间的稳定状态,这说明在相平面中的任何起始条件下,系统都将趋近于极限环进行振荡.图4(c)表示系统处于双向连续波区(bi-CW),即发生霍普夫分岔之前的运动状态.2个模式的波将逐渐趋于一个相同的稳定状态,同时相位也趋于0,在这一状态下,两模式的相位差锁定为0,此环形谐振器可以用作光陀螺仪器的应用,用来检测旋转的角速度[7-8].图 4(d)表示在无向锁定区(UNI)系统的运动状态.可以观察到在这一区域出现了光学模式锁定现象,这在文献[5]中有详细的描述,即系统的其中一个模式消失,而另一个模式达到高强度.具体哪一个模式获得增强、哪一个模式消失则取决于系统的起始状态.另一个重要的结果是锁定后两模式的相位差变为π/2−这一稳定值,研究光陀螺仪器的众多理论文献就这一相位差跳变现象进行了理论研究.从分岔角度,可以归结为极限环的极限点突变.这一重要的突变发生前的系统状态表示为图 4(e)和(f).可见在通过这一突变点时,系统逐渐从近似正弦波(见图4(b))形态,经过三角波状态(见图 4(e)),最终演变为方波状态(见图 4(f)).这与文献[3]中的实验结果相一致.
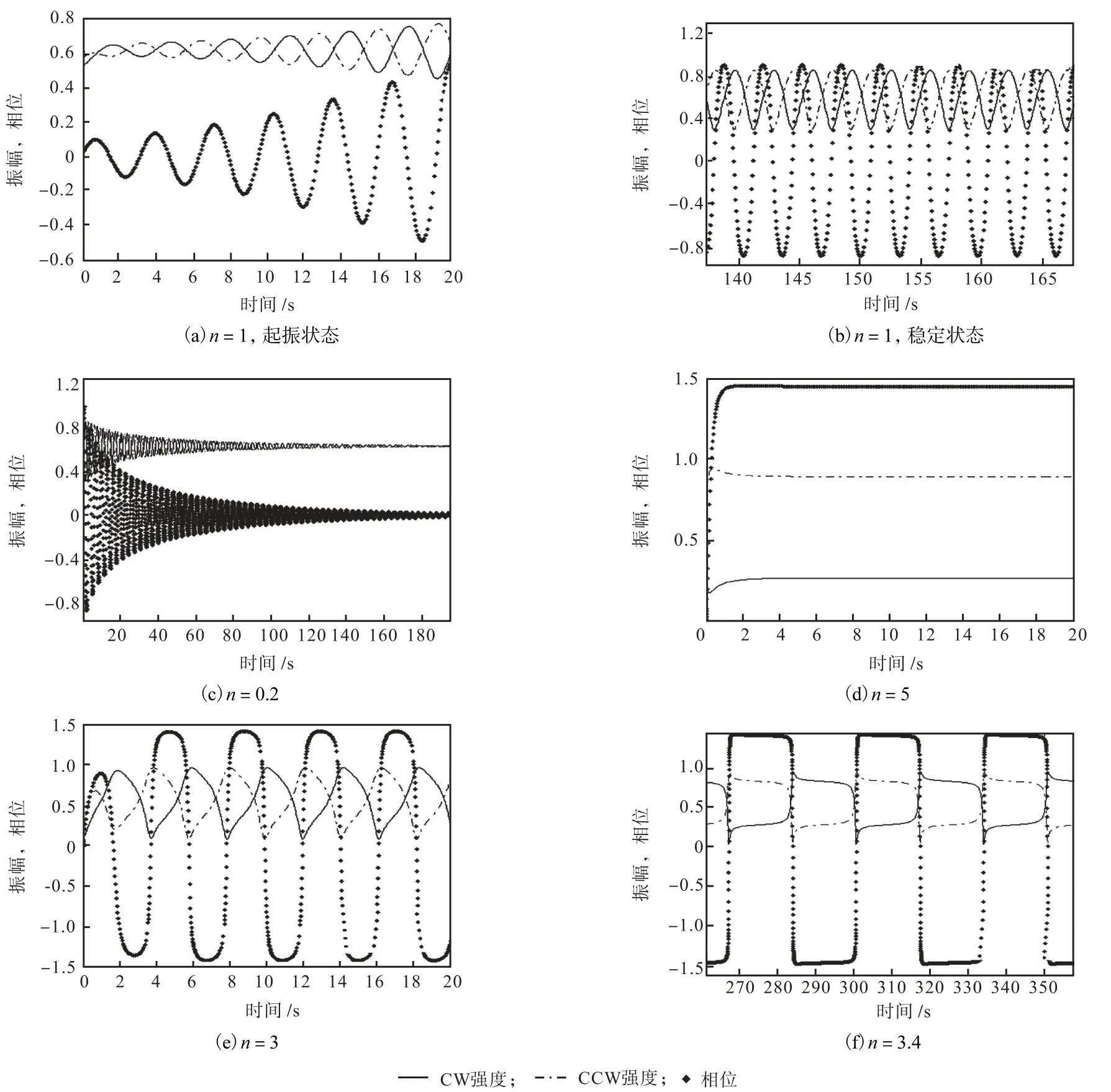
图4 系统在不同泵浦参数n下随时间变化的非线性运动Fig.4 Nonlinear movements of the system with time with various pump parameters
前面指明背散射效应和光学增益饱和效应的相互竞争导致了上述复杂的非线性运动.其中背散射效应是由于波导输出耦合部分和散射中心等不完美性的统计性结果.从性质上分成守恒的背散射和耗散的背散射 ,两者的作用是不同的.守恒的背散射项的相位为π/2,耗散的背散射项的相位为0.
一般地说,正反馈将导致系统双稳态现象(滞后的转换)而负反馈将导致振荡现象.环形谐振器系统中,正反馈是由增益饱和效应引发的,文献[11]就这一过程进行了描述,即系统将最终处于某一模式的锁定态.外部光注入可以加速这一锁定过程,也是通过这一锁定过程实现的[6].具体的正反馈回路可以这样进行说明:如果其中一个模式 E1的光得到增强,式(1)中的交叉耦合项将导致另一模式 E2的减少,而模式E2的减少也会通过交叉耦合使E1获得增强.所以将产生双稳态现象.
负反馈情形下的守恒的背散射和耗散的背散射所起到的作用是不同的,可以用图5中所示复平面下的复数矢量来表示.其中E1和 E2为两模式矢量,Ec1和Ec2分别表示两模式的守恒背散射项影响,它以导数项的形式减少相反模式的振幅的变化速率;Ed1和Ed2分别表示两模式的耗散背散射项的影响,它以导数项的形式减少相反模式的相角的变化速率.
耗散的背散射提供了振幅的负反馈,即模式|E1|增加会通过Ed1导致|E2|的减少,另一方面|E2|的减少又会通过Ed2使得|E1|进一步减少.它和增益饱和机制的竞争将使得2个模式的振幅稳定在一定的数值上.
守恒的背散射则提供了相角的负反馈,通过这一机制一个模式的增强将增加或减小另一个模式的旋转速度,最终的结果是使得两者以相同的速率旋转.这一效应是双向连续波区发生相位锁定的根本原因.
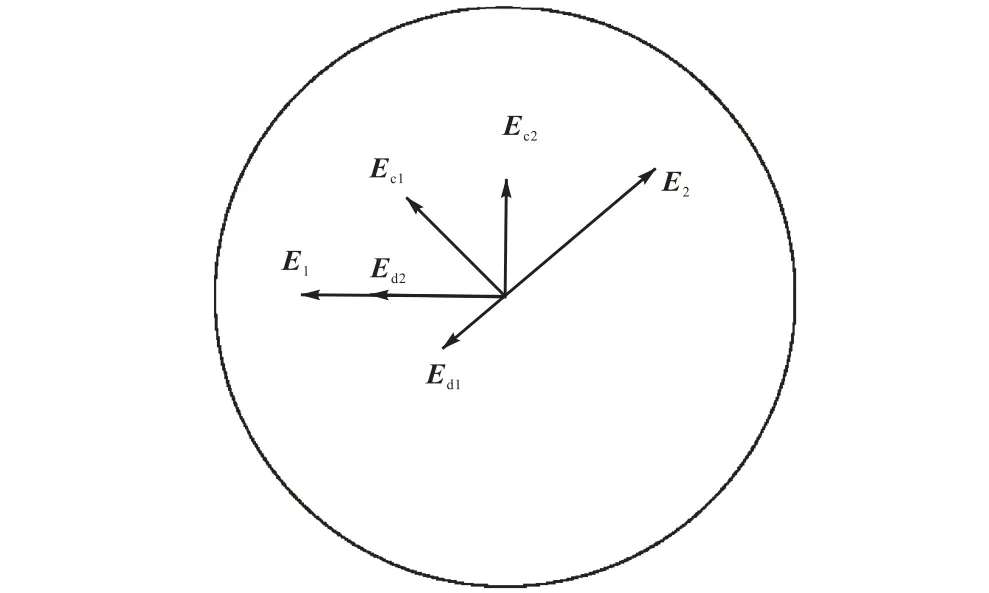
图5 2种背散射项的复平面表示Fig.5 Complex plane expression of two kinds of backscatter parameters
进一步可以得到极限环振荡周期和泵浦参数之间的关系,如图6所示.在极限环的极限点附近,振荡的周期将发生急剧的增加.对应庞加莱截面(见图3(a))极限环在相平面中的面积不断增加,即振荡变得越来越慢.这一现象和文献[4]实验的结果相一致.
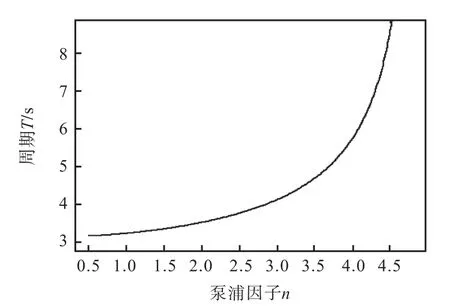
图6 极限环周期和泵浦因子参数之间的关系Fig.6 Relationship between limit cycle period and pump parameter
笔者也计算了背散射参数的幅值和相角参数变化导致的分岔区域变化的情况.所有霍普夫分岔点形成的平面之下是双向连续波区域.通过不断变化背散射参数后计算霍普夫分岔点可得到这一重要曲面.极限环的极限点随背散射参数变化关系为图 7的曲面,在曲面以上为无向锁定波区域.计算这一曲面的方法是:从霍普夫分岔点开始,逐步增加泵浦参数,通过格龙库塔积分法计算系统的瞬态解,经过相当长的一段时间后进行随机采样,如果采样点的均方差落入一个很小的范围,则可判定为系统进入锁定区.反复扫描背散射参数,可以得到无向锁定区的边界曲面.这样得到了图 7所示的系统分区图.在霍普夫分岔点曲面和极限环极根点曲面之间的部分是双向互振荡区,从图7中可以观察到这3个区域并不一定同时存在,在一定的参数变化范围内出现 3个区,而在另一参数变化范围内只出现2个区域(双向连续波区和无向锁定区).因此可以得出结论:背散射的性质将引发半导体环形谐振器的不同行为.
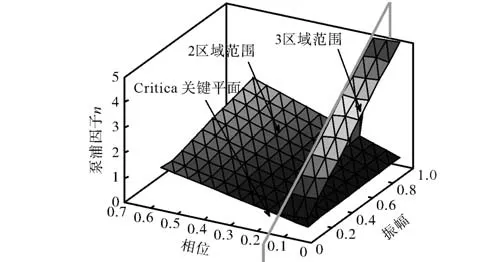
图7 背散射参数变化的系统分区示意Fig.7 Operation regions with variation of backscatter parameters
在图 7中还可以观察到无向区边界曲面在特定相角下的突然下降,如果器件工作在相角参数附近,系统的行为将对外界噪声的变化非常敏感.系统在实际情况下将呈现混沌的特性.
3 结 语
本文运用现代非线性动力学理论,对半导体环形激光器的模型进行了稳定性和分岔行为的研究.结果表明:守恒的背散射和耗散的背散射在这一复杂的非线性运动中提供了不同的负反馈机制,而光学增益饱和则提供了正反馈的机制,由于这些机制的相互作用,模型中泵浦参数的变化将导致霍普夫分岔以至混沌等复杂的非线性运动.观察到极限环的极限点附近振荡的周期急剧增加,以及背散射参数的幅值和相角参数变化导致的分岔区域将导致出现两区域和三区域的不同情况.
[1] Hill M T,Dorren H J S,de Vries T,et al. A fast lowpower optical memory based on coupled micro-ring lasers [J]. Nature,2004,432(7014):206-209.
[2] Liu Y,Hill M T,Calabretta N,et al. Three-state alloptical memory based on coupled ring lasers[J]. IEEE Photon Tech Lett,2003,15(10):1461-1463.
[3] Sorel M,Laybourn P J R. Alternate oscillations in semiconductor ring lasers[J]. Optics Letters,2002,27(22):1992-1994.
[4] Sorel M,Giuliani G,Scire A,et al.Operating regimes of GaAs-AlGaAs semiconductor ring lasers:Experiment and model[J]. IEEE J Quantum Electron,2003,39(10):1187-1195.
[5] Sorel M,Laybourn P J R,Giuliani G,et al. Unidirectional bistability in semiconductor waveguide ring lasers[J]. Appl Phys Lett,2002,80(17):3051-3053.
[6] Yuan Guohui,Yu Siyuan.Bistability and switching properties of semiconductor ring lasers with external optical injection[J]. IEEE J Quantum Electron,2008,44(1):41-48.
[7] Kuznetsov Y A.Elements of Applied Bifurcation Theory[M]. 3rd ed. New York:Springer,2004.
[8] Numai T.Analysis of signal voltage in a semiconductor ring laser gyro[J]. IEEE J Quantum Electron,2000,36(10):1161-1167.
[9] Spreeuw R J C,Centeno Neelen R.Mode coupling in a He-Ne ring laser with backscattering[J].Physical Review A,1990,42(7):4315-4324.
[10] Dennis M L,Diels J M. Analysis of a ring-laser gyroscope with intracavity phase conjugate coupling[J]. Applied Optics,1994,33(9):1659-1672.
[11] Tang C L,Schremer A,Fujita T.Bistability in two-mode semiconductor lasers via gain saturation[J]. Appl Phys Lett,1987,51(18):1392-1394.

