数字化X射线成像系统MTF的刀口测量法

龚绍润，高 峰，徐雅洁

(天津大学精密仪器与光电子工程学院，天津 300072)

调制传递函数(modulation transfer function，MTF)是对线性影像系统空间频率传输特性的定量描述，是影像评价方法中的重要进展．此前普遍使用定性描述指标，例如影像密度、对比度、清晰度、分辨率及失真度等来评价成像系统的影像质量，但其结果受个人主观因素影响大．近年来随数字化CR、DR成像技术的迅速发展，MTF作为客观指标已成为放射成像工作者和研究者所关注的重要影像评价手段．同时，MTF也是获得成像系统探测量子效率(detective quantum efficiency，DQE)、噪声功率谱(noise power spectra，NPS)及噪声等价量子数(noise equivalent quanta，NEQ)的必需参数．

要定量地评价DR系统的固有成像质量，只需计算不受个人主观因素影响的系统固有预采样MTF(pre-MTF)[1]，为简明起见，文中所有 pre-MTF均用MTF表示．实际中系统MTF常由以下3种扩散函数来计算 ：点扩散函数(point spread function，PSF) 、线扩散函数[5](line spread function，LSF)和边缘响应函数(edge respond function，ERF)[6-8]，它们分别描述经成像系统后点、线和边缘弥散程度，能够间接地反映系统成像能力．

狭缝法(slit camera)和刀口法(edge)已被国际放射学会公认为是获得 MTF的较好方法，日本将狭缝法定义成测量 MTF的标准方法[1]，刀口法也已被国际电气技术委员会(IEC)指定为测量系统 MTF的标准方法[6,9-10]．将通过狭缝法和刀口法所获得的同一系统下不同 MTF曲线进行比较，可知前者在高频域有较高信噪比，而后者在低频域有较高信噪比[7]．通过狭缝法获得的系统MTF精确，且操作简便、方法成熟．但因其加工难度高(狭缝宽度≤10mμ，误差在1mμ内)，导致在实际应用中此法较难被推广．由于刀口法测量仪器自加工相对容易，在科研实验和常规检测中被广泛使用．

对通用X 射线成像设备进行MTF测量时，测量条件和参数选择对最终 MTF测量结果影响较大，所以在IEC标准中对其进行了严格规定[11-13]，对不同级别测量要求做了详细说明．例如在 1994年版的IEC61267里就规定了标准射线等级的要求，包括对应距离参数、射线等级编号、X射线管电压、半值层、附加过滤层和标准规定的信噪比(signal-noise ratio，SNR)．上述规定只适用于通用 X 射线成像设备，非通用设备中很多关键参数如光束大小及强度与通用设备差别很大，所以对于非通用设备如乳腺 X 射线成像系统和小动物放射成像系统等其他专用的设备上述测量标准已不再适用．由上可知，在评估实验室小动物放射成像系统成像质量时无法遵从上述标准实行，而只能进行定量分析，无法将其结果与其他成像系统进行横向对比．因此，笔者利用刀口法对 MTF进行相对测量．虽然本文讨论的是基于常规接触模式下系统 MTF测量，但此方法将为今后在相衬成像模式下定量评估系统成像质量提供指导和帮助．

1 刀口法测量系统MTF

通常刀口方向与图像采样方向存在一定角度，如图 1所示，要想得到精确的边缘响应函数 ERF必须对刀口附近图像进行过采样[1,6]，经插值拟合成ERF(x)．想从边缘响应函数 ERF(x)运算得到线扩散函数 LSF(x)，对ERF(x)进行差分运算或使用卷积滤波器[-0.5，0，0.5]均可．

LSF(x)函数经傅里叶变换后再取模，就能得到其调制传递函数

中FT为傅里叶变换．通常在描述系统调制传递函数时使用归一化处理后的结果，其公式为

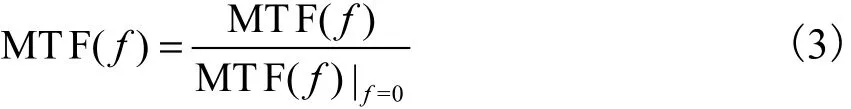
一般来说，调制传递函数低频域主要决定图像的对比度，高频域决定图像细节的重现能力及边缘处清晰度．从 MTF曲线的包络面积可判断系统成像质量优劣，通常希望成像系统 MTF曲线包括的面积越大越好．

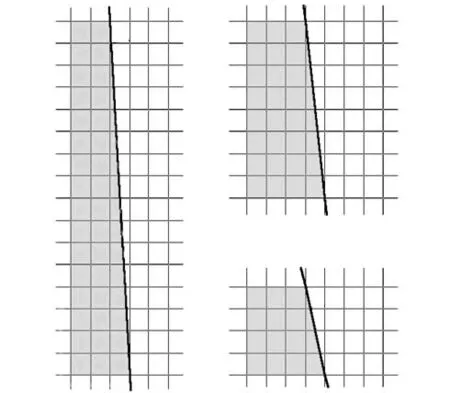
图1 产生ERF曲线的数值模型Fig.1 Numerical model for ERF curves

2 采样率及噪声对系统MTF的影响

利用过采样重构ERF，需将刀口与探测器矩阵成一定倾角摆放[1,6,10]，通常将仪器边缘和数字化探测器阵列方向之间倾角 α 保持为2°～6°(对应插值数为9～29 条)，理论上 α 越小(插值数越高)所获曲线就越精确，但实际中常由于探测器自身各像素点响应差异性及刀口加工精度不高等问题的存在导致获得的LSF曲线剧烈振荡，最终影响系统MTF曲线的准确性．下面将借助数值模拟工具来研究采样率及噪声对系统MTF曲线的影响．

2.1 过采样ERF重构方法

图1中各子图的灰色部分均表示铅板覆盖区域，粗黑线表示经同轴准直和理想切割后的刀口边缘．图 1(a)、图 1(b)和图 1(c)为采用刀口法进行 16条、8条和 4条插值时(对应的倾角α 分别为 3.58°、7.13°和 14°)的示意图．采用16条插值来重构过采样ERF曲线如图1(a)所示，对应插值顺序从1到16，然后从17到32，依此类推完成整条ERF曲线的重构．

2.2 模拟模型中各参数选择及处理方法

模拟真实情况下经铅板衰减后的强度值和未经铅板衰减的“空载”强度平均值分别为50和13,000(实验系统使用的为 14位模数转换器，其强度为13,000时仍工作在[0，16,384]线性响应范围内)．假设各像素点偏移量及响应特性完全一致，无噪声时刀口边缘处各像素点的强度值为 50x＋13,000(1-x)(最简便的处理方式是假设强度响应等于不同衰减下强度值乘以其对应的面积百分比之和，此处x表示该位置上铅板覆盖区域占单个像素面积百分数)．重构过采样ERF曲线时，宽度固定为3.2,mm(对应插值的列数为 64)，也就是说采用 16条插值时矩阵大小为16×64(重构后 ERF长度为 1,024)，8条插值时矩阵为 8×64(重构后 ERF长度为 512)，4条插值时矩阵为4×64(重构后ERF长度为256)．考虑到实际成像中 X射线落在相应像素区域内被记录前，会在穿过荧光屏过程中与材料相互作用导致 X射线束弥散(满足高斯分布)，故将插值后 ERF曲线与荧光屏PSF做卷积即可获得重构后 ERF．参照实验室小动物放射成像系统中探测器像素点大小和荧光屏材料及厚度，选择模拟中像素大小为 50,μm，荧光屏 PSF半高宽(full width at half maximum，FWHM)为100,μm．为模拟真实探测器噪声对系统ERF及MTF的影响，根据实际探测过程中铅板区域和“空载”区域噪声水平添加随机噪声，铅板区域随机噪声方差为50×0.2，“空载”区域随机噪声方差分别选取13,000×0.005、13,000×0.01进行研究．

2.3 MTF曲线分析

图 2(a)、图 2(d)和图 2(g)分别为 4条、8条和16条插值时在无噪声、0.5%噪声及 1%噪声下获得的ERF曲线，虽然对应于右端“空载”区出现较高噪声，但仍较好地完成了对 ERF曲线的采样．与图2(b)、图 2(e)和图 2(h)比较不难看出，无噪声情况下4条插值时由于采样间距较大，并未能采样到LSF曲线的峰值，此处验证了插值条数越高对 LSF曲线描述越精确，但却同时发现在高插值数下其 LSF曲线右端“空载”区噪声越明显．根据奈奎斯特准则，空间域的非足够采样将导致信号在频率域的混叠，这将严重影响MTF曲线在高频域的准确性．在过采样情况下，将多条过采样 ERF曲线取平均值再做差分运算即可减少单条LSF曲线右端的噪声水平．此处的模拟研究中并未采用任何降噪措施，图2(b)、图2(e)和图2(g)对应不同插值数和噪声水平下的MTF曲线．

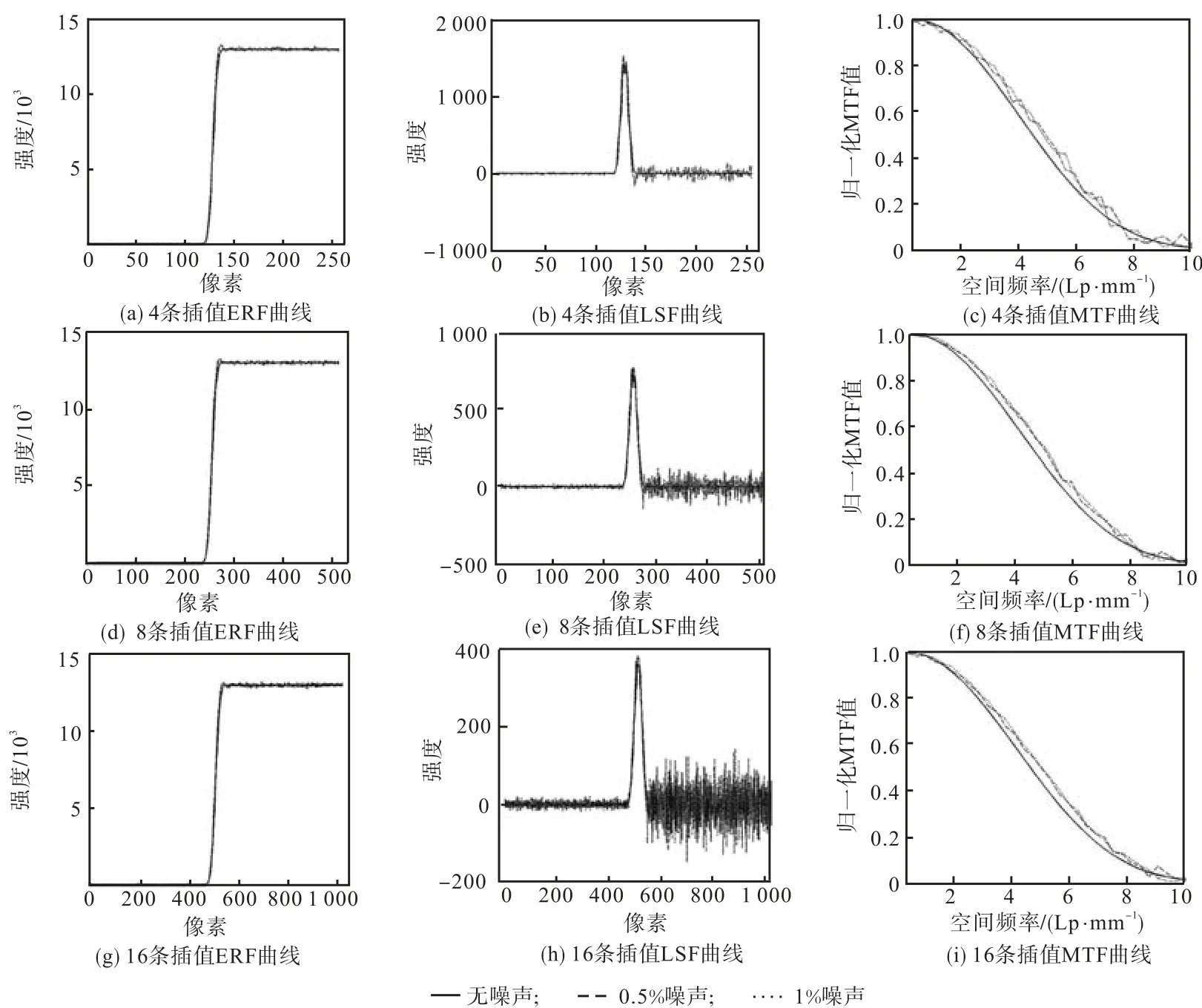
图2 不同采样率及噪声水平下ERF、LSF和MTF曲线Fig.2 Curves of ERF, LSF and MTF under different sampling rates and noise levels

图 2(c)、图 2(f)和图 2(i)中由于模拟像素点大小为 50,μm，可知其对应极限频率为 10,Lp/mm(line pair per millimeter，每毫米内线对数)，从图中不难看出系统 MTF值在 10,Lp/mm时已几乎为零．为进行定量分析可将图 2(c)、图 2(f)和图 2(i)中不同插值数及噪声水平下几个离散空间频率对应的MTF值整理成表 1．从前面理论分析过程不难得出：无噪声情况下插值数越高时，获得的MTF与系统理想MTF值越接近．图 2(c)和图 2(f)中 4条和 8条插值情况下的无噪声MTF值均小于图2(i)中16条插值无噪声MTF值，且两者相较 16条插值下 MTF值的相对偏差随着空间频率值增高不断增大．引入表 2中均方根误差来定量描述不同噪声水平与无噪声时MTF的偏离量，假设16条插值下无噪声MTF为真实值．从表 2数据不难看出：无噪声时插值数越大，相对“真实值”均方根误差越小；然而在相同噪声下，插值数越大时其均方根误差越大．为减少由于非充分采样引入的频率混淆及过采样下噪声对结果的影响，实验中将采用多条过采样 ERF曲线取平均后的结果来计算系统MTF值．

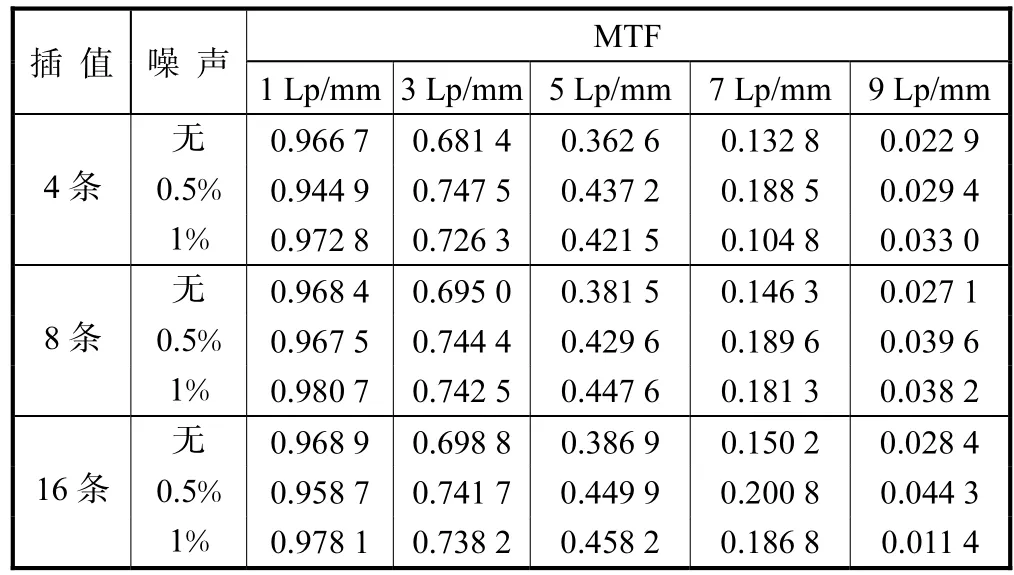
表1 在不同噪声水平下各空间频率对应的MTF值Tab.1 MTFs under different spatial frequencies and noise levels

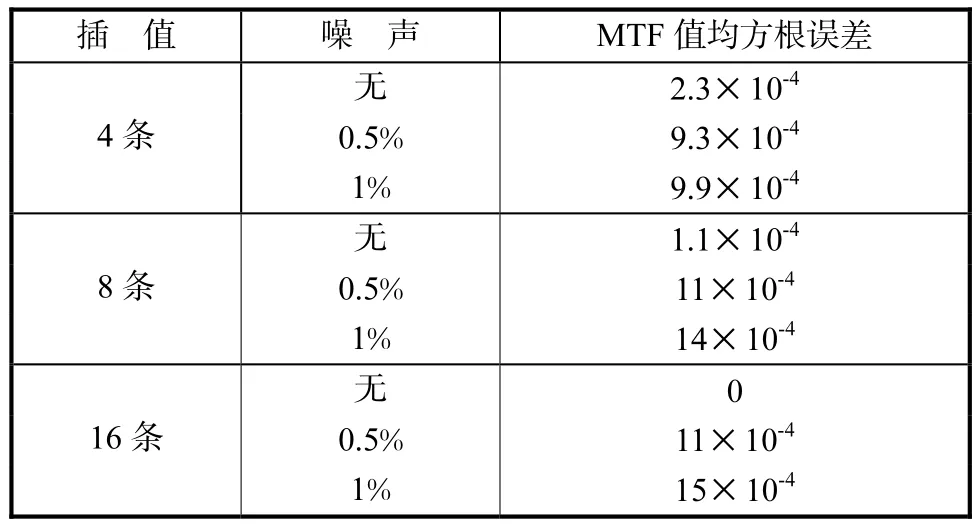
表2 不同噪声水平下各插值数对应的均方根误差值Tab.2 Root mean square errors under different noise levels and interpolations

3 实验准备

由于CMOS比CCD在价格、能耗及数字化处理速度等方面都占有优势，图3(a)所示DR成像系统选用了CMOS探测器．系统相关指标如下：X射线阳极采用钨靶，并带有0.2,mm厚铍窗，标称微焦点源直径50,μm，点源空间半角β＝10.8°，140μm厚材料为氧硫化二钆的 Kodak荧光屏，CMOS探测器有效像素点大小为50μm(对应fNyquist＝10,Lp/mm)，管电压在5～45,kV内可调，管电流固定为0.5,mA，曝光时间在0.1～19.9,s内可调．图 3(b)所示的探测器 D可通过移动轴在与微焦点源S距离为 0.6～1.8,m范围内自由移动．该系统现在主要被用于X射线相衬成像方法的研究，本文做常规接触模式下系统MTF测量研究是为今后在相衬成像模式下定量评估系统成像质量奠定实验基础．文中所有实验将探测器保持在最高位置，使其到微焦点源S的距离固定为 0.6,m．为减少光源曝光随机性影响，文中用于计算 MTF值的图像均为 10幅图像求和后再取多段过采样 LSF曲线的平均结果．实验中其他参数的选择如下．

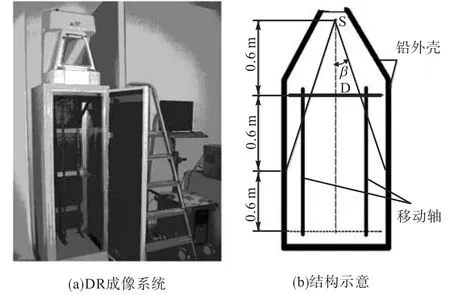
图3 DR成像系统及其结构示意Fig.3 DR imaging system and its sketch

3.1 曝光管电压及曝光时间

管电压及时间的选择从以下2方面综合考虑：探测器上不放置任何物体(空载)时强度图像的均匀性和各管电压下产生 X射线光子能量的分布范围．表3为不同曝光管电压及曝光时间下成像中心区域强度标准差与其平均值百分比．

表 3数据反映出 CMOS板响应的均匀性．使用33,kV和35,kV曝光管电压时，任何曝光时间下获得的图像均匀性明显好于25,kV和30,kV时．在此无需考虑更高管电压情况，因为管电压越高产生的光子穿透力越强，会增加LSF曲线高频噪声．从图4不同管电压产生 X射线光子能量分布范围可知[14]，当管电压为33,kV时，其产生的光子能量峰值出现在25,keV左右，适用于乳腺或其他软组织成像，为系统用于乳腺成像研究奠定了基础．

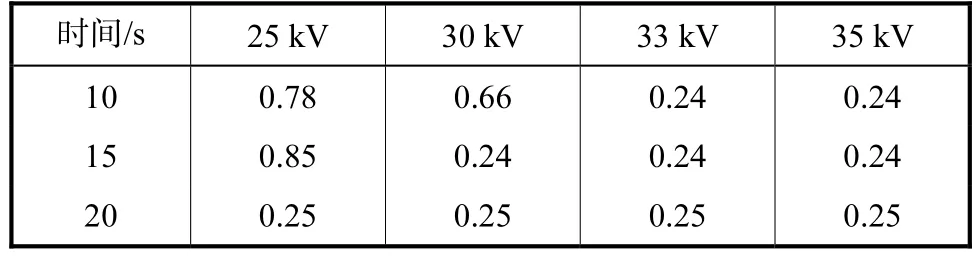
表3 不同条件下成像中心区域强度标准差与其平均值百分比Tab.3 Percentage of the intensity’s standard deviation to its mean value in the central imaging area under different tube voltages and exposure time%

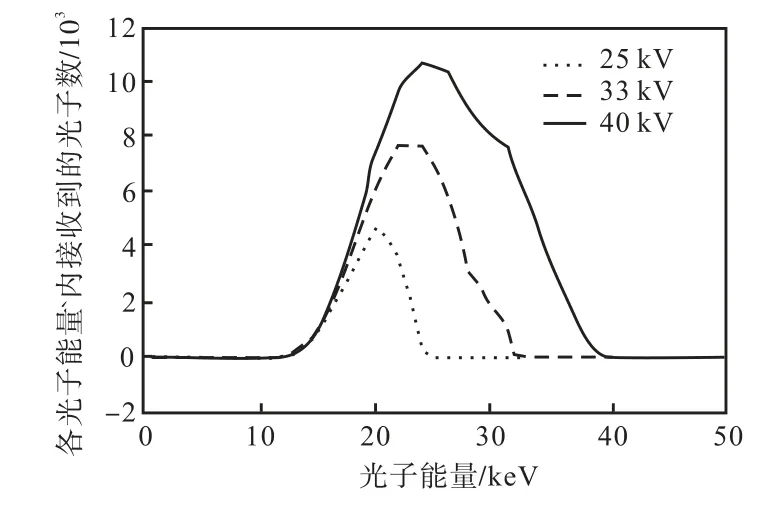
图4 不同管电压下X射线光子能量分布Fig.4 Photon energy distributions of X-ray under different tube voltages

3.2 刀口法测量材料的选择

刀口法测量材料的选择对最终MTF值也有较大影响，需综合考虑材料相对该曝光管电压下 X射线的衰减特性及材料厚度对 LSF曲线两方面的影响．根据不同材料对X射线的衰减程度高低不同，可将所获图像分为黑白过渡和灰白过渡2种情况，灰白过渡(仍有部分 X射线穿过材料)会导致最终 MTF值高频分量偏高[6]．表 4是选取曝光管电压 33 kV、曝光时间为10 s时，不同材料和不同厚度下感兴趣区域强度平均值、标准差及偏差百分比．

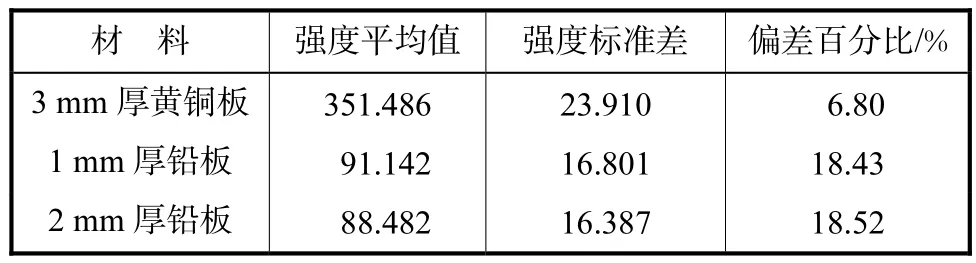
表4 不同材料不同厚度下感兴趣区域强度平均值、标准差及偏差百分比Tab.4 Intensity’s mean values，intensity’s standard deviations，and percentages of the standard deviation to its mean value of different materials with different thickness in the interest area

从表4不难看出，选择铅板材料时其图像强度平均值和标准差均小于黄铜板，较低平均值和较小方差能够减少最终 MTF值高频误差．1,mm 厚铅板的强度平均值和标准差与 2,mm厚铅板相差无几，考虑到实际中将厚铅板完全摆放水平具有相当难度，倾斜时ERF引入的误差会严重影响 MTF值，所以实验中选择1,mm厚铅板进行MTF相对测量．

4 实验结果分析及讨论

为了更直观地对传统成像质量评估方法和 MTF客观评价方法进行比较，首先使用线对卡来分析系统的成像质量，随后介绍了使用刀口仪器有效测量系统MTF值的方法．

4.1 线对卡分析

实验仿体为 Gammex公司 X射线测试模型MA0647，该模型对 X射线强吸收材料为金镍合金，线对卡的测试范围为5～20,Lp/mm．图5为曝光管电压 33,kV、曝光时间 10,s条件下获取的图像．调整图像窗宽和窗位后，利用肉眼尚可清楚分辨出9,Lp/mm，然而对于10,Lp/mm时则比较模糊，可见利用此高精度线对卡进行系统成像质量评价时受主观因素的影响较大．从图 6中 5～11,Lp/mm 强度剖面图可清楚分辨出 5～9,Lp/mm的强度剖面图，10,Lp/mm 时强度对比度已不太高，利用此强度剖面图分析后仍说明采用线对卡评估时最终成像质量受主观因素影响较大．图6中11,Lp/mm的线对卡图像对比度已被严重破坏，无法正确辨认．

图5 线对卡图像Fig.5 Image of the test line pair card

首先根据 5～11,Lp/mm 强度剖面中数据定位到每个线对图像处，找到某一空间频率下最小值和其周围的最大值，从每个空间频率下的最小值和最大值转换成表 5中对应调制度．以上数据不难证明，空间频率值增大时其对应调制度不断减小，由于到 11,Lp/mm 时对应的调制度已经下降到 1.14%，导致最终线对卡图像已经无法辨认．

图6 线对卡5～11 Lp/mm图像强度剖面图Fig.6 Intensity profiles of the test card in the range from 5 Lp/mm to 11 Lp/mm

表5 不同空间频率对应的调制度Tab.5 Modulation degrees under different spatial frequencies

4.2 MTF测量

图 7所示刀口法测试仪器是将经微纳设备加工后的黄铜及铅板材料与有机玻璃支架组装而成，支架上放置的刀口测试材料可随时更换为黄铜板或铅板，实验中需将精细加工后刀口放置于视场中心，利用支架上的3颗螺丝可对整个测试仪器进行水平性调整．

图7 刀口法测试仪器Fig.7 Equipment used in the edge measurement

实验中将刀口边缘和 CMOS探测器阵列方向摆放成 3.57°，对应插值数为 16条．图 8(a)为经软件自动拟合生成的曲线．图 8(a)中 ERF曲线较光滑，清楚地展示了刀口边缘突变效应．对 ERF曲线做差分或卷积滤波后再经长度截断可得图 8(b)LSF曲线，不难发现图中 LSF曲线左右两端的高频噪声较大，而且中心位置的冲激响应也出现急剧变化，这是由于精细加工刀口面不平整所致．图8(c)中MTF曲线的低频区衰减较快，在 5 Lp/mm 的空间频率处其MTF值已经衰减到 0.3以下，与线对卡在 5 Lp/mm的 MTF值 0.38相差较大，获取的 MTF值和线对卡值在10 Lp/mm时都衰减到0.07左右．该结果中由于包括了LSF曲线中高频噪声影响，致使对系统成像质量的评价不够准确．

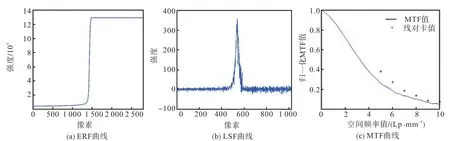
图8 倾角3.57°时利用刀口法获得的ERF、LSF及MTF曲线Fig.8 Curves of ERF, LSF and MTF with the edge positioned at a slight angle of 3.57° to the detector array

前面实验结果可说明，由于倾角 3.57°较小(插值数16条)，CMOS探测器上各像素点响应差异性较大导致LSF曲线高频噪声较大(如图8(b)中LSF曲线所示)，最终求得的MTF曲线与表5中数据相差太大，没能正确反映出系统成像能力．下面对实验结果进行指数校正．首先根据 ERF曲线的特征将其分成左、中、右 3大段．随后分别对 ERF曲线左侧和右侧进行指数拟合，曲线两侧的细小波动经处理后基本为一条直线，再在最小二乘法的指导下，对 ERF曲线的阶跃响应采用分段指数拟合，拟合结果见图 9(a)．拟合前后 ERF曲线重合度较高，在强度值[1,250，12,260]阶跃变化段，经指数拟合前后的均方根误差为72.6，相对于突变强度值来说是较小的，数据拟合极大地减少了像素点差异性引入的奇异值．图 9(b)中未截断拖尾的LSF曲线是从经指数拟合后的ERF曲线差分后获得的，与图8(b)中LSF曲线相比，高频噪声得到抑制．随后为解决红色LSF曲线左侧的延伸，采用设定阈值截断并对截断部分进行指数延伸后可得到图9(b)中截断拖尾后的 LSF曲线．图 9(b)中原始LSF曲线和拟合后LSF曲线的峰值和附近点强度值都较好地吻合．从图 9(c)中不难看出，后者较前者在[0,Lp/mm，8,Lp/mm]范围内MTF响应均要高一些，与线对卡值较接近．说明原始 ERF曲线经指数拟合后能够消除因刀口加工精度不高引入的奇异点，然后将LSF曲线拖尾截断再经指数延伸后能够提高MTF的低频响应值并降低高频噪声的影响．将最终 MTF曲线和线对卡值进行比较不难观察到，前者略微低于后者，源自于此测试方法仍存在一些不可避免的系统误差，例如：倾斜角度摆放随意导致插值非整数而产生的系统误差；由于载物台的存在导致刀口边缘距探测器有一定距离，且距离越大导致最终 MTF的测量误差越大[7]．利用本文介绍的方法适当地选择倾角后，再对原始 ERF曲线进行指数函数分段拟合，然后对LSF曲线拖尾截断获得图9(c)中MTF曲线，相对于图 8(c)已更为接近系统MTF值，证明了利用该实验方法及测量材料模型可以更为准确地得到 X射线成像系统 MTF曲线，说明此方法和实验操作对获取 MTF曲线的可行性及有效性．要想通过此法获取系统精确MTF值仍需克服刀口法自身的缺陷及机械加工上的配合，例如克服因插值非整数产生的系统误差、强衰减材料及其厚度的选择、刀口边缘加工精度、探测器和刀口摆放时相对于光源的水平性判断等诸多因素．

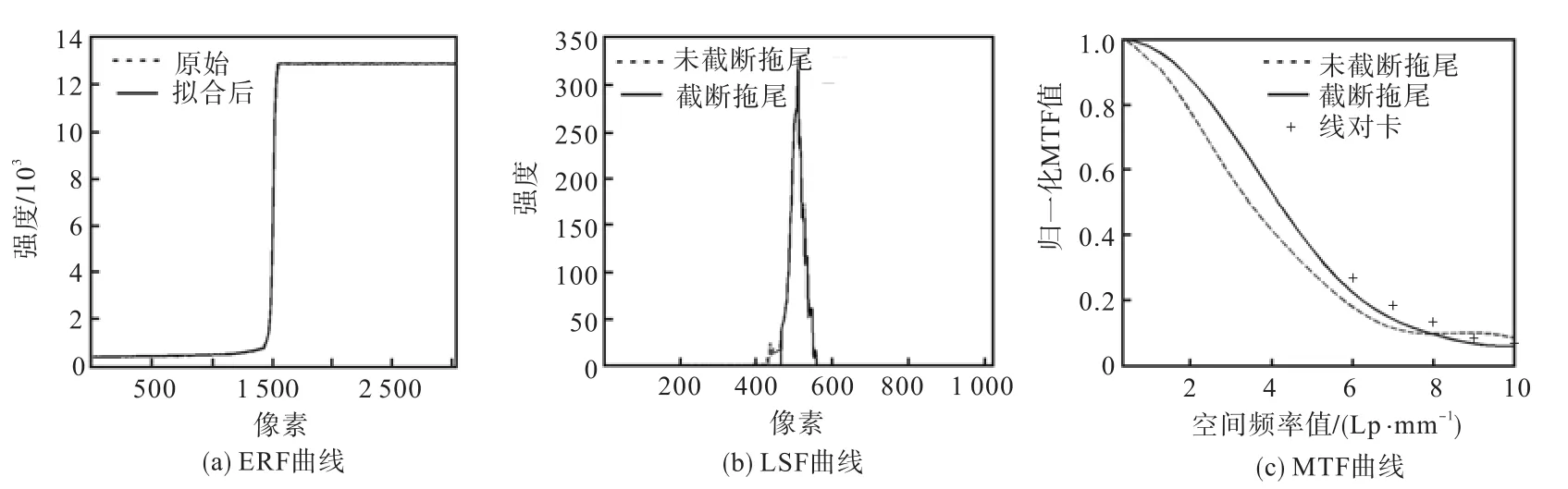
图9 经指数曲线拟合及截断拖尾后获得的ERF、LSF及MTF曲线Fig.9 Curves of ERF, LSF and MTF after exponential curve fitting and tail portion truncating

5 结 语

采用刀口法适当选择倾角(4°左右)，对原始ERF曲线进行指数拟合并对 LSF曲线拖尾截断，能够有效地测量DR系统的MTF曲线．选择合适的倾角能保证满足奈奎斯特采样频率的要求，减少信号混叠，通过采用多条过采样 ERF曲线取平均值在一定程度上抑制由于探测器本身各像素点响应差异性引入的高频噪声影响，然后对原始 ERF曲线利用指数函数进行分段拟合后再截断 LSF曲线拖尾现象可以提高 MTF低频响应并抑制高频噪声的影响，实验结果给出了系统较为准确的 MTF曲线．综上所述，利用文中介绍的方法对DR系统的MTF值进行有效测量是可行的．

［1］ Fujita H，Tsai D Y，Itoh T，et al. A simple method for determining the modulation transfer function in digital radiography[J]. IEEE Transactions on Medical Imaging，1992，11(1)：34-39.

［2］ 康立丽，邓晓刚，陈 阳，等. 影像系统 MTF算法实现及分析[J]. 北京生物医学工程，2002，21(3)：180-182.

Kang Lili，Deng Xiaogang，Chen Yang，et al. The implementation and analysis of MTF algorithm of imaging system[J]. Beijing Biomedical Engineering，2002，21(3)：180-182(in Chinese).

［3］ 梁丽红，路宏年. X射线数字成像系统传递函数模型[J]. 北京航空航天大学学报，2005，31(9)：1018-1021.

Liang Lihong，Lu Hongnian. Transfer function model on X-ray digital radiography system [J]. Journal of Beijing University of Aeronautics and Astronautics，2005，31(9)：1018-1021(in Chinese).

［4］ 叶 昶，仲爱军，骆清铭. 用于小动物研究的数字 X线成像系统[J]. 中国医疗器械杂志，2004，28(3)：179-182.

Ye Chang，Zhong Aijun，Luo Qingming. A digital radiography system for small animals and specimen imaging[J]. Chinese Journal of Medical Instrumentation，2004，28(3)：179-182(in Chinese).

［5］ 周俸才，管永红. 闪光 X 射线照相系统调制传递函数测量[J]. 光子学报，2001，30(2)：218-224.

Zhou Fengcai，Guan Yonghong. Modulation transfer function measurement of flash X-ray radiographic system[J]. Acta Photonica Sinica，2001，30(2)：218-224(in Chinese).

［6］ Samei E，Flynn M，Reimann D. A method for measuring the presampled MTF of digital radiographic systems using an edge test device[J]. Medical Physics，1998，25(1)：102-113.

［7］ Illers H，Buhr E，Gunther-Kohfahl S，et al. Measurement of the modulation transfer function of digital X-ray detectors with an opaque edge-test device[J]. Radiation Protection Dosimetry，2005，114(1/2/3)：214-219.

［8］ Zhu Yuemin，Kaftandjian Valerie，Peix Gilles，et al.Modulation transfer function evaluation of linear solidstate X-ray-sensitive detectors using edge techniques[J].Appl Opt，1995，34(22)：4937-4943.

［9］ Tatsuya Yamazaki，Makoto Nokita，Shinsuke Hayashida，et al. A method to measure the presampling MTF using a novel edge test device and algorithm[C]// Medical Imaging 2004：Physics of Medical Imaging. San Diego，CA，USA：SPIE，2004：696-704.

［10］ Cunningham I A，Reid B K. Signal and noise in modulation transfer function determinations using the slit，wire，and edge techniques[J]. Medical Physics，1992，19(4)：1037-1044.

［11］ Samei E，Dobbins J，Saunders R，et al. IEC 62220-1：Medical electrical equipment—Characteristics of digital X-ray imaging devices(Part 1)：Determination of the detective quantum efficiency[C]// International Electrotechnical Commission(IEC)．Geneva，Switzerland，2003.

［12］ Illers H，Buhr E，Hoeschen C. Measurement of the detective quantum efficiency (DQE)of digital X-ray detectors according to the novel standard IEC 62220-1[J].Radiation Protection Dosimetry，2005，114(1/2/3)：39-44．

［13］ Olivo A，Arfelli F，Cantatore G，et al. An innovative digital imaging set-up allowing a low-dose approach to phase contrast applications in the medical field[J]. Medical Physics，2001，28(8)：1610-1619.

［14］ Boone J M，Seibert J A. An accurate method for computer-generating tungsten anode X-ray spectra from 30 to 140 kV[J]. Medical Physics，1997，24(11)：1661-1670.