观音岩水电站混合坝插入式接头的抗震性能

熊 堃，何蕴龙，曹学兴

(武汉大学水资源与水电工程科学国家重点实验室，武汉430072)

观音岩水电站位于云南省丽江市华坪县与四川省攀枝花市交界的金沙江中游河段，为金沙江中游河段规划8个梯级电站的最末一个梯级，上游与鲁地拉水电站相衔接．最大坝高为168,m，电站装机容量为3,000,MW．挡水建筑物系由碾压混凝土重力坝及右岸心墙堆石坝组成．从地质条件来看，由于右岸坝基承载力不足，只能布置心墙堆石坝，这就要求设计混凝土坝和心墙堆石坝的软硬接头．本工程处于高烈度地震区，在参考国内外的设计经验以及计算分析[1-2]的基础上，将软接头设计成心墙包裹混凝土坝上游面的插入式[3]，接头最大高度为 71,m．软接头是工程的薄弱环节，而坝址区设计地震峰值加速度达 0.229g，如何保证接头结构的动静安全是关系到工程全局的重大工程技术问题．

笔者对大坝连接坝段进行了三维非线性静力分析，并采用时程法对大坝连接坝段进行三维地震动力分析，以揭示在设计地震过程中接头部位接触面的开合变形性态、剪切破坏及地震永久变形情况．此外，还通过提高地震输入加速度峰值，考察接头部位的极限抗震能力，并对土石料 Hardin本构模型以及接触面模型的相关参数进行了敏感性分析．根据所得动力分析成果，对大坝软接头的抗震性能及抗震安全性进行评价．

1 基于薄层单元的接头接触面模拟

插入式接头具体结构如图1所示.

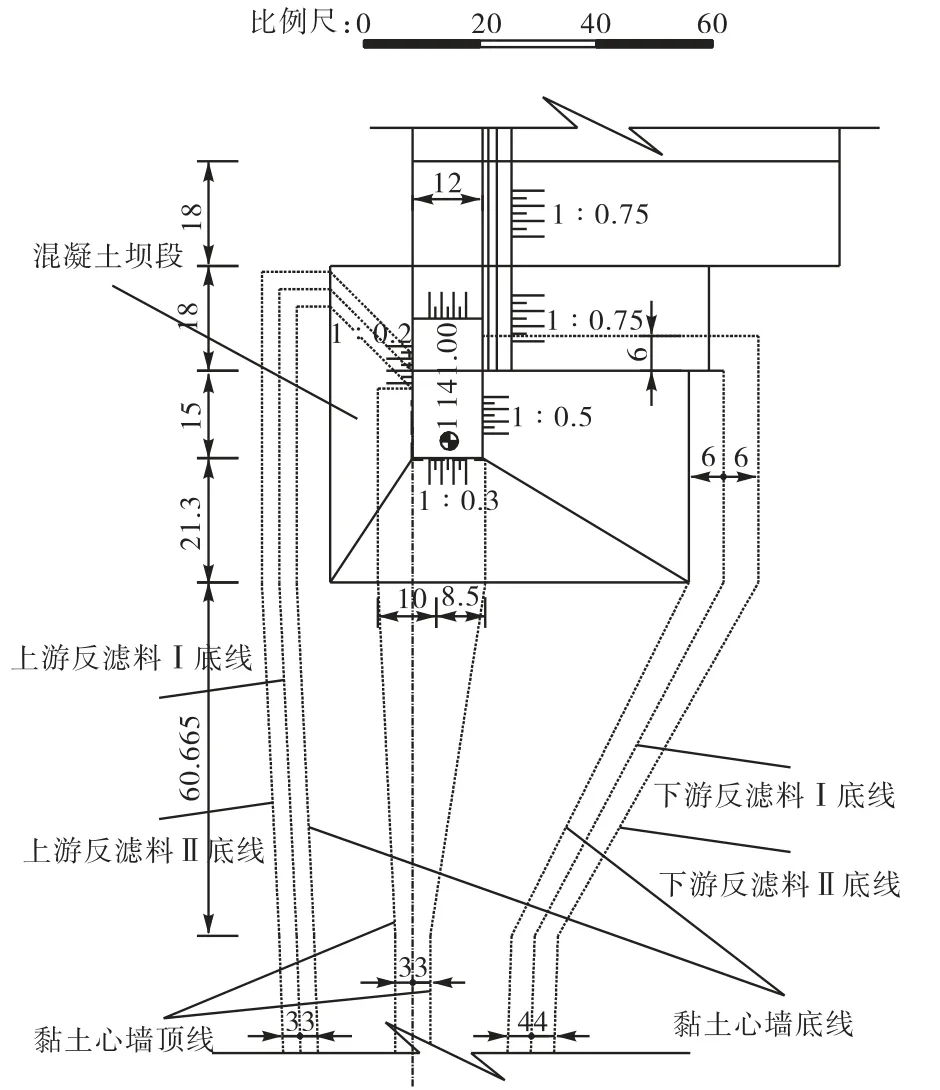
图1 插入式接头结构(单位：m)Fig.1 Structural diagram of the inserted junction(unit：m)

在混合坝的接头部位，由于混凝土与心墙的材料性质差别较大，插入堆石坝的混凝土坝段与心墙之间的接触面在地震等荷载的作用下，会表现出与连续体不同的剪切滑移、脱开等特殊的变形特征，因此，应采用特殊的接触面单元来加以模拟．有代表性的接触面模型有无厚度的 Goodman单元模型[4]和有厚度的Desai薄层单元模型[5]．在以往的计算中，接触面的模拟常采用无厚度的Goodman单元，其参数易定，受到广泛应用，但因单元无厚度，接触面两侧单元会发生在法向的嵌入，不得不靠人为地调整法向刚度的取值来解决．Desai等提出的薄层单元，能模拟土与结构相互作用破坏时，常发生在附近土体薄层范围内剪切错动的现象，但薄层厚度的取值具有很强的经验性．

在本文中，接头部位的接触面采用薄层单元进行模拟，此单元在刚度矩阵形成方面与普通单元一样，但在本构矩阵中，将法向和切向分量分开来考虑．采用薄层单元的形式可以很好地反映接触中的剪切错动带，更符合土与混凝土接触问题的实际情况；并且，在计算中当接触单元在法向受压时，不必人为地设定很大的法向刚度系数，计算更为合理．对于薄层单元的厚度，Desai建议厚度 t＝(0.01～0.1)B[5]，根据文献[6]的研究，在不产生显著误差的情况下，应使厚度尽可能的小．

设薄层单元沿接触面法线方向，即 z′方向应变均匀分布，忽略垂直于厚度方向的变形模量及其耦合作用，则薄层单元增量形式的本构关系可表达为

式中：Dnn为薄层单元法向弹性模量；Dns为剪切模量．

薄层单元法向应力应变关系，借鉴 Bandis[7]等关于岩石节理法向变形的双曲线模型，即

式中：σn为法向正应力：ΔVj为法向变形：a为法向初始刚度的倒数，即 1/Kni；a/b为应力应变双曲线的渐近线，即法向最大压缩量Vm．则可得法向刚度为

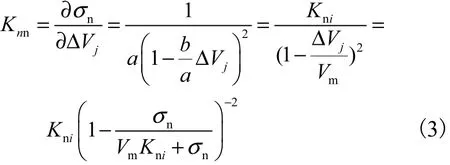
在法向压缩变形接近最大压缩量时，法向刚度会很大，使接触面自动满足在法向不会发生嵌入的条件．按照文献[8]，可将法向刚度转化为法向弹性模量表示，即

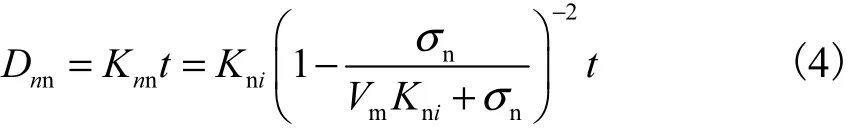
式中t为薄层单元厚度．

薄层单元切向应力应变关系，采用文献[9]的剪切双曲线模型，即

式中：τ为切向剪应力；dh为剪切破坏发生前的剪切变形；常数m为初始剪切刚度的倒数；n为τ-dh双曲线的水平渐近线的倒数，即 n =1/τult＝Rf/τp，Rf为破坏比，τp为临界剪应力，按摩尔库伦定律计算为τp=c−σnt anφ.则切向刚度可转化为切向弹性模量表示[9]，即

式中：Ksi为初始切面刚度系数；ap为大气压力．

在计算过程中根据薄层单元的法向正应力判断单元处于何种状态之中，具体见表 1．其中σn受压为负，受拉为正．

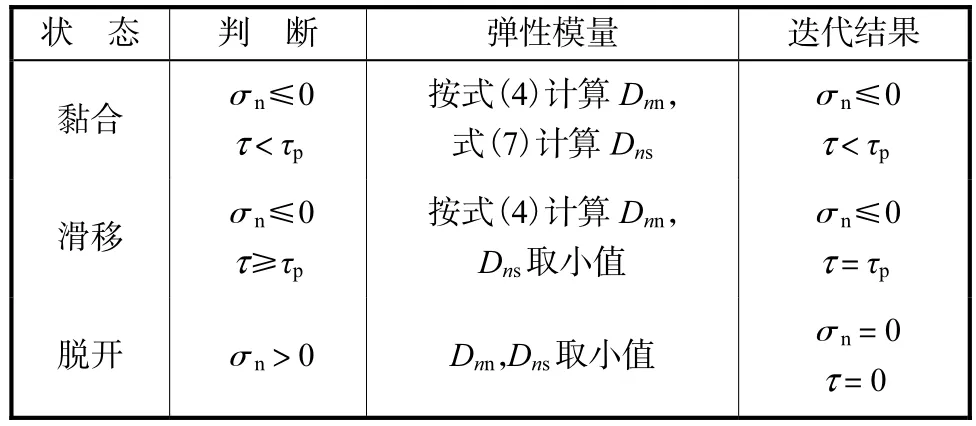
表1 接触单元状态说明Tab.1 Illustration of the contact element

此外，除了模拟接触面法向、切向刚度的非线性变化，还在薄层单元中加入了阻尼成分以模拟动接触问题中能量耗散问题．在动力计算过程中，接触单元的阻尼矩阵以Rayleigh阻尼表示，其中阻尼比取为接触面附近土的阻尼比，随着动剪应变的增大而非线性减少．实际计算中阻尼比非线性问题利用等效线性化的方法处理．

2 计算模型与计算参数

2.1 计算条件

根据中国地震局地质研究所完成的《金沙江观音岩水电站工程场地地震安全性评价和水库诱发地震评价报告》，坝址场地的地震基本烈度为Ⅶ度，基准期100年超越概率为2%的基岩场地水平加速度峰值为 0.229g，基准期 100年超越概率为 1%的基岩场地水平加速度峰值为 0.270g．由《水工建筑物抗震设计规范》(DL5073—2000)，观音岩大坝设计地震取基准期 100年超越概率 2%，校核地震取基准期100年超越概率为1%．

综合考虑观音岩坝址的地质结构、潜在震源的震级及震中距等因素，选取了美国 Taft地震波、人工地震波与云南丽江地震波共 3条地震波进行分析．计算时将地震加速度峰值加速度调整至 0.229g，输入历时取30 s．根据计算结果，输入Taft地震波所得接触面反应较其他两条强烈，故本文中主要就Taft地震波所得计算结果进行分析．其中计算所取 Taft地震波顺河向加速度过程线如图2所示．

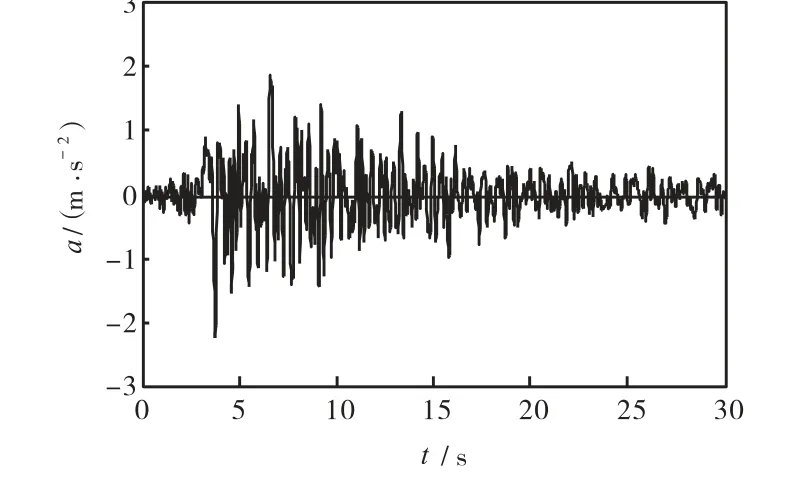
图2 Taft地震波顺河向加速度过程线Fig.2 Time history of transverse acceleration of Taft earthquake wave

2.2 计算模型

堆石及心墙料的静力本构关系采用 Duncan E-B模型[10]．动力计算中，坝体堆石与心墙料采用 Hardin非线性动力本构模型[11]．Hardin模型是一种等效黏弹性模型，它紧紧抓住了土在动力情况下非线性和滞后性2个主要特点，采用随剪应变幅和有效应力状态而变化的等效弹性模量和等效阻尼比来表达．模型概念明确，应用方便．Hardin模型中土在周期荷载作用下的应力应变骨干曲线为双曲线型，其动剪应力与动剪应变的关系为

式中：dτ为动剪应力；dγ为动剪应变；G0为起始剪切模量；τy为最大动剪应力．将 G0坡度线与 τy水平线的交点的横坐标称为参考剪应变fγ，则fγ=,τy/G0．可得动剪切模量为

其中起始动剪模量G0计算公式为

式中G0、0σ′和pa采用同一量纲．

阻尼比的计算式为

式中λmax可根据试验确定或经验公式计算．

静动力计算中，基岩和混凝土均采用线弹性模型，混凝土密度取2,400,kg/m3，弹性模量取25.5 GPa，泊松比0.167，动弹性模量在静弹性模量的基础上提高30%．静动力计算的参数见表 2，心墙与混凝土重力坝接触面参数见表 3．堆石与心墙料归一化的动剪切模量、阻尼比与动剪应变的非线性关系如图3所示．

目前，基于Serff等 提出的应变势概念的整体变形计算方法有着广泛的应用．本文主要就整体变形计算方法中的软化模型来计算堆石坝的地震永久变形．计算时，根据试验结果，残余体应变 εv与动剪应力比Δτ/σ0′、残余轴向应变 εp与动剪应力比Δτ/σ0′的关系可用幂函数形式近似表示，即

具体参数见表4．

表2 材料参数Tab.2 Material parameters

表3 接触面单元计算参数Tab.3 Calculation parameters for contact elements

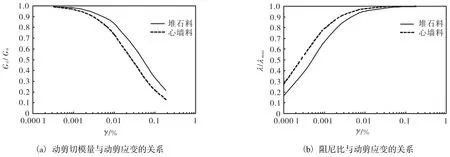
图3 动剪切模量、阻尼比与动剪应变的非线性关系Fig.3 Nonlinear relationship between shear modulus and damping ratio versus shear strain

表4 残余应变计算参数Tab.4 Calculation parameters for residual strain

2.3 有限元模型

有限元模型主要采用8结点6面体单元，为适应边界过渡采用了部分棱柱体单元．模型共有单元63,381个，结点 58,354个，图 4为有限元网格．接头心墙与混凝土接触面如图5所示，其中心墙与混凝土对接面为第1接触面，心墙外包混凝土的上游面为第2接触面．

图4 有限元网格模型Fig.4 Finite element mesh model

在动力计算中，地基范围在坝基面以下取1倍坝高，上下游方向各延伸 1.5倍坝高，基础底部为固定约束，基础四周为法向约束．为了消除坝基对地震动的放大作用，采用无质量地基方案进行分析，只考虑坝基岩体的弹性作用．

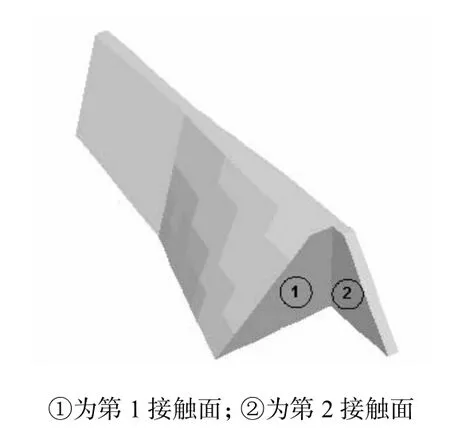
图5 接触面示意Fig.5 Illustration for contact surfaces

3 接触面动力反应分析

在接触面上取 3个典型接触点对以进行具体分析，接触点对 a位于第 1接触面的坝顶中央，接触点对b和c分别位于第1接触面和第2接触面坝顶中央以下，其高程为正常蓄水位．

3.1 接触面脱开度分析

表5列出了两接触面的最大脱开度及时间．

表5 接触面最大脱开度Tab.5 Maximum detachments of the contact surfaces

3.1.1 第1接触面

图6为第1接触面上2个典型接触点的脱开时程，文中选取了地震较为强烈的 2～12,s进行分析．图中可以看出，在地震波作用下，由于土和混凝土材料性质的差异，心墙与混凝土坝段接触面的顶部中央和接触面内正常蓄水位高程位置均出现了脱开和压紧相间的情况，但脱开度较小；并且，与接触面顶部相比，接触面内正常蓄水位高程位置脱开的次数与脱开持续时间明显较少．在30,s的地震过程中，第1接触面的顶部中央出现的最长脱开时间为 1.52,s，而正常蓄水位高程位置出现的最长脱开时间为0.36,s．

图 7(a)为第 1接触面的最大脱开度包络图，由图可知在地震过程中，坝顶、接触面上游侧边缘及下游侧出现了脱开，接触面边缘的部分比接触面内部开度大，整个接触面上最大脱开度出现在坝顶的上游侧，为 2.7,mm．图 7(b)为接触点对 b出现最大连续脱开时间时的接触面开度情况，此时坝顶附近脱开部分面积较大，但并未完全贯通，最大脱开度同样出现在坝顶的接触面上游侧，为 1.8,mm．图 7(c)和(d)分别为接触点对a和b出现最大脱开度时，整个接触面的脱开情况．在3种情况下，接触面上游边缘均脱开．

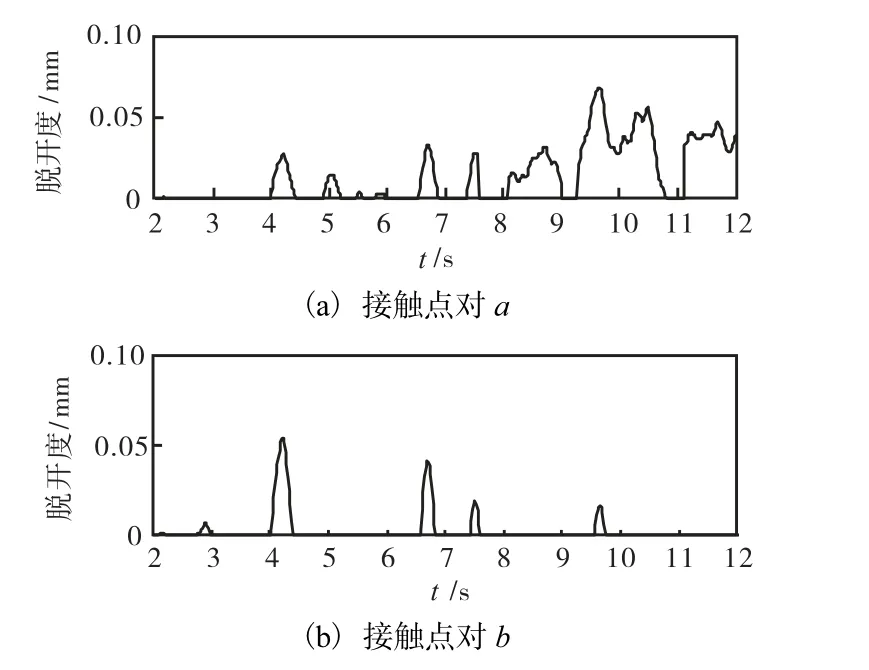
图6 第1接触面典型接触点对的开合时程Fig.6 Time history of the typical points’ detachments on Fig.6 the first contact surface

图7 第1接触面开度(单位：mm)Fig.7 Detachments of the first contact surface(unit：mm)

3.1.2 第2接触面

图8为心墙与混凝土坝段的第2接触面中，正常蓄水位高程位置在地震过程中的脱开时程，同样也是给出了地震最为强烈的 10,s历时．从计算结果可以看出，在地震波作用下，接触点对 c也出现了脱开和压紧相间的情况．在 30,s的地震过程中，该位置出现的最长脱开时间为0.92,s．

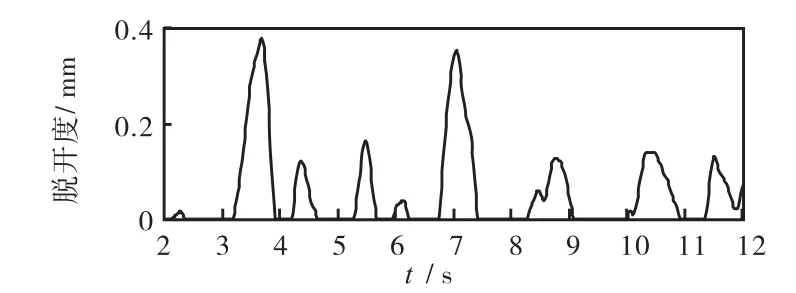
图8 第2接触面接触点对的开合时程Fig.8 Time history of the typical points’ detachments on the second contact surface

图 9(a)为第 2接触面的最大脱开度包络图，由图可知，在地震过程中，坝顶及接触面靠堆石坝一侧出现了脱开，而且接触面边缘的部分明显比接触面内部开度大，脱开的范围也比内部大．整个接触面上最大开度出现在坝顶的靠堆石坝一侧，为 3.25,mm．图9(b)为接触点对 c出现最大连续脱开时间时的接触面开度情况，此时靠堆石坝一侧有最大值为 0.6,mm的脱开，接触面内部的坝顶仍有一定范围的脱开，但开度很小．图9(c)和(d)分别为接触点对a和b出现最大脱开度时，第 2接触面的脱开情况，在这二种情况下，接触面内部有脱开，两侧边缘仍是压紧的．

3.2 剪切破坏分析

在接触面上定义应力水平为

式中：ϕ和 c为摩擦角和接触面黏聚力．当 S达到1时，说明接触面发生了滑动破坏．图 10显示了地震过程中接触面上的最大应力水平分布．在第 1接触面上，靠下游的边缘出现了剪切破坏；在第 2接触面上，接触面中部靠重力坝的方向出现了一定范围的剪切破坏．

3.3 永久变形分析

表 6列出了第 1接触面各方向的永久变形最大值，在地震以后，其顶部有较明显的永久变形，主要表现为在顺河向朝上下游变形，顺坡向下变形，以及在法向张拉变形．表 7列出了第 2接触面各方向的永久变形最大值，在震后接触面的顶部有较明显的永久变形，主要表现为在横河向朝堆石坝变形，顺坡向下变形以及在法向张拉变形．

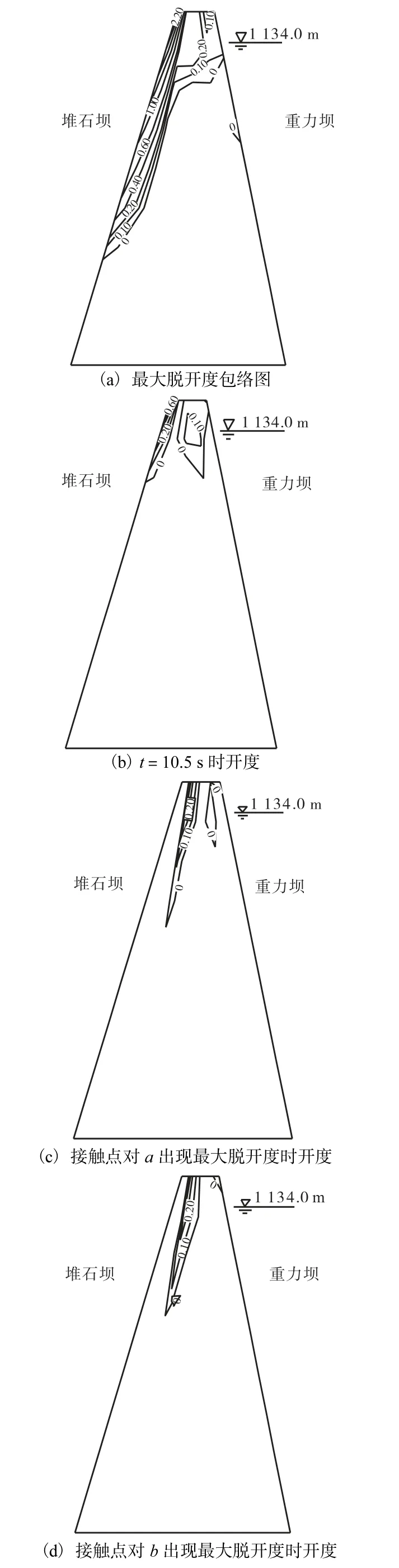
图9 第2接触面开度(单位：mm)Fig.9 Detachments of the second contact surface(unit：mm)

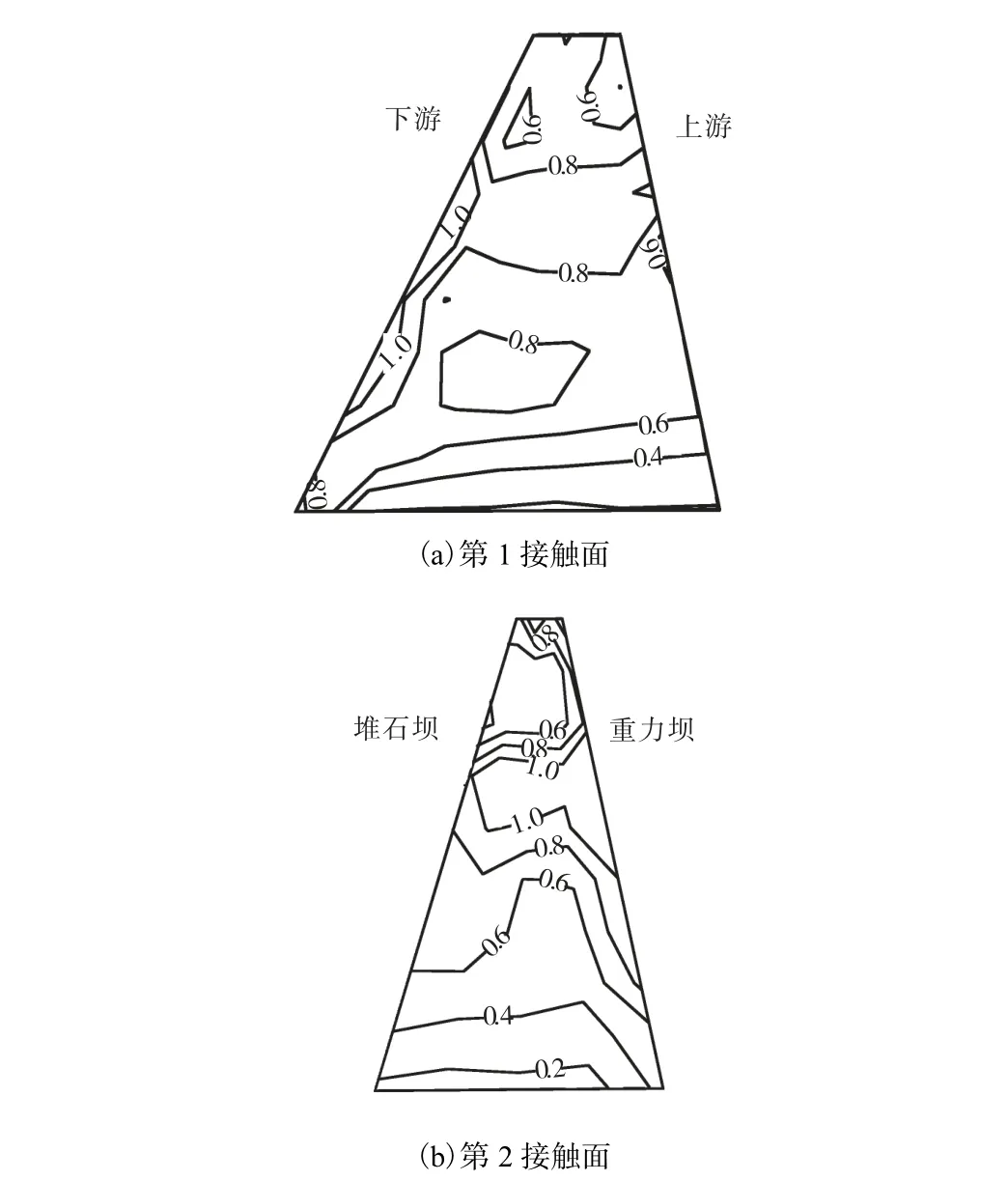
图10 接触面最大应力水平Fig.10 Maximum stress level of the contact surfaces

表6 第1接触面永久变形最大值Tab.6 Maximum seismic residual deformation of the first Tab.6 contact surface cm

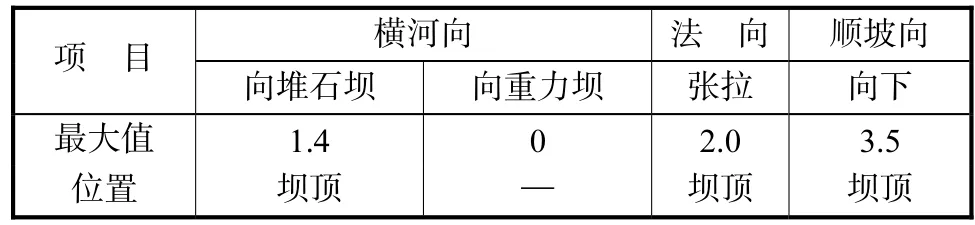
表7 第2接触面永久变形最大值Tab.7 Maximum seismic residual deformation of the second contact surface cm

4 接触面极限抗震能力分析

不断增大输入地震加速度的峰值，以考察接头接触面的极限抗震能力．在输入不同加速度下第 1接触面的脱开情况如图 11所示，剪切破坏情况如图 12所示．接触面具体脱开情况及剪切破坏面积见表8．

输入加速度为0.229g时，最大脱开度为2.7,mm，在接触面的中心线上、正常蓄水位以下3,m均为脱开的范围，但脱开度大于 0.5,mm 的范围仅限于坝顶接触面上下游的边缘．当输入加速度增大到0.270g时，最大脱开度增加到 3.39,mm，增加了约 26%；脱开的范围明显增大，接触面的中心线上、正常蓄水位以下10,m 均为脱开的范围，接触面下游边缘均脱开，坝顶接触面的上下游脱开度大于0.5,mm的区域也有一定的扩展．当输入加速度增大到0.4g时，最大脱开度增加到5.17,mm，相对于输入加速度为0.229g时增加了1倍；脱开的范围继续增大，接触面的中心线上、正常蓄水位以下 12,m 均为脱开范围，接触面的上下游边缘脱开度大于 0.5,mm 的区域有明显的扩展，接触面下游边缘脱开度增大．

输入加速度为 0.229g时，接触面上仅有下游边缘发生了剪切破坏，加速度增大到 0.270g时，破坏区域由下游向上游扩展．随着输入地震的增大，接触面上剪切破坏的区域逐渐扩展，剪切破坏范围主要在坝体的中部．输入加速度为0.4g时，接触面上半部则几乎已经全部被剪切破坏．

表8 不同地震输入下接触面脱开情况及剪切破坏面积Tab.8 Detachments and shear break areas of contact surfaces under different earthquakes

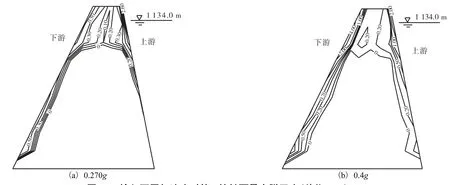
图11 输入不同加速度时第1接触面最大脱开度(单位：mm)Fig.11 Maximum detachments of the first contact surface under different earthquakes(unit：mm)

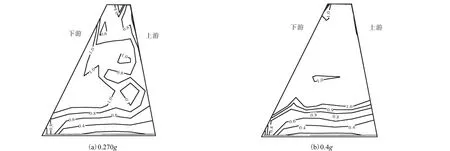
图12 输入不同加速度时第1接触面剪切破坏情况(单位：mm)Fig.12 Shear break areas of the first contact surface under different earthquakes(unit：mm)

5 接触面脱开度的敏感性分析

由于在计算中运用了土石料的非线性静动本构以及非线性的接触面模型，考虑到计算参数一定程度的不确定性，下文对土石料 Hardin本构模型以及接触面模型的相关参数进行了敏感性分析．根据以往研究经验，选取了 Hardin模型的参数 C和λmax、接触面模型的初始刚度系数、抗剪强度参数和接触面的厚度进行敏感性分析，主要考察这些参数在一定范围变化时接触面开度的变化情况．

通过对 Hardin模型的参数敏感性分析可知，当参数 C和λmax变化时，第 1与第 2接触面的开度情况显示出基本一致的规律，都是在接触面顶部及两侧开度较大，表9列出了接触面最大脱开度以及特征点的具体开度值．参数 C主要体现了土石料剪切模量的变化，λmax主要体现了阻尼的变化．由表知，当 C值增大时，接触面的最大脱开度增大，C值减小时最大开度减小，并且变化较为明显；而 C值的变化对接触面内部 3个特征点的开度则影响相对较小．最大阻尼比λmax对接触面开度值的影响没有剪切模量显著，但也有一定程度的影响．

通过对接触单元模型的参数敏感性分析可知，各种参数变化后，接触面开度所显示的规律仍基本一致，依然是在接触面顶部及两侧开度较大，并且接触面边缘的最大开度值随参数变化较大，接触面中央的开度值随参数变化较小．对于各种参数而言，抗剪强度参数对接触面开度的影响较小，而初始刚度系数及薄层单元厚度的影响较大．表 10列出了接触面最大开度以及特征点的具体张开值．由表中可知，当薄层单元厚度变大时，接触面的开度均减小；厚度变小时，开度则增大．当初始切向刚度系数增大时，接触面的开度增大；系数减小时，开度亦减小．当初始法向刚度增大时，接触面的开度减小；刚度减小时，开度增大．然而，以上开度值均没有量级上的改变．

表9 Hardin模型参数对接触面及接触点对最大开度敏感性分析Tab.9 Sensitivity analysis of the parameters in Hardin constitutive model on the maximum detachments of the contact surfaces and typical points

表10 接触单元参数对接触面及接触点对最大开度敏感性分析Tab.10 Sensitivity analysis of the parameters in contact elements on the maximum detachments of the contact surfaces and typical points

由以上敏感性分析可知，各种主要参数在一定范围内变化时，2个接触面的开度分布规律是一致的，接触面仅在靠近顶部和两侧部位发生一定程度的张开，但随着各参数的变化，具体开度值有所变化，而数量级基本不变．由文献[11]可知，在国内经历过地震考验的混合坝接头有辽宁三道岭大坝与甘肃碧口大坝．三道岭水库位于辽宁省营口县，距离海城地震震中18,km，坝址烈度8度．右坝头为混凝土溢流坝，以混凝土重力坝和混凝土心墙插入与土坝心墙相接，与观音岩工程的接头型式相同，连接处坝高 17.0,m．震后混凝土坝与土坝连接部位没有损坏，但在接触面上形成肉眼可见的裂缝，缝的深度达到 l,m 以上，运用中未发现漏水异常，说明这种结构形式具有一定的抗震能力．而甘肃省碧口水电站土石坝右坝端与溢洪道的翼墙相连接，接头型式与观音岩工程不同，其经过 1976年 8月松潘地震考验，未发现变形或裂缝．因此，本文中接触面的计算结果在定性上与实际震害现象是较为一致的，计算结果所反映的规律与结果应较为正确，但具体数值等定量上的正确性仍期待在实践中进行进一步的检验．

6 结 论

(1)在设防烈度地震作用下，土质防渗体与混凝土坝接触面仅在靠近顶部和两侧部位发生一定程度的张开，张开开度较小，张开持续时间短，张开度大于0.5,mm 的区域局限在接触面两侧较小范围内，并且在地震过程中接触面尤其正常蓄水位以下接触面并未形成贯通的张开面．此外，在心墙下游设置了 2层反滤层，并且在与插入段接触面附近处其厚度均由4,m变厚为6,m，下游内侧反滤层完全包裹插入段，而下游外侧反滤层则全包裹内侧反滤层，可以有效保护黏土心墙和接触面，达到滤水不滤土的目的，并促使可能出现的裂缝自愈，不会使心墙的细粒料流失而发生渗透破坏．因此，接头的抗震安全性是有保障的．

(2)在设防烈度地震作用下2个接触面出现了较小范围的剪切破坏．地震以后接头部位2个接触面的顶部有较明显的永久变形，变形的趋势主要是水平沿接触面向两侧、顺坡向朝下以及法向张拉变形．

(3)即使对应于 9度强震，接头部位工作状况虽有恶化，但并不存在即刻发生灾难性破坏的条件，震后及时降低库水位至开裂范围以下，可以防止接头发生进一步破坏；震后接触面裂缝修复难度较小，可以方便及时完成相关修复工作，恢复大坝正常运行．

(4)Hardin模型和接触单元模型的各种参数变化后，接触面开度所显示的规律仍基本一致，依然是在接触面顶部及两侧开度较大，但随着各参数的变化，具体开度值有所变化，而数量级则基本不变．接触面抗剪强度参数对接触面开度的影响较小，而接触面初始刚度系数、薄层单元厚度以及土石料的动剪切模量的影响较大．

［1］ 周 伟，常晓林，周创兵，等. 观音岩水电站混合坝接头结构形式研究[J]. 岩土力学，2008，29(2)：496-500.

Zhou Wei，Chang Xiaolin，Zhou Chuangbing，et al. Study on configuration shape of concrete connection of Guanyinyan mixed dam[J]. Rock and Soil Mechanics，2008，29(2)：496-500(in Chinese).

［2］ 彭云枫，何蕴龙，李建成. 混合坝接头型式与抗震安全性分析[J]. 武汉大学学报，2008，41(3)：60-63.

Peng Yunfeng，He Yunlong，Li Jiancheng. Structural patterns of junction of composite dam and aseismic safety[J]. Engineering Journal of Wuhan University，2008，41(3)：60-63(in Chinese).

［3］ 潘昌勇，柴余松. 观音岩水电站混凝土重力坝与土石坝接头型式研究[J]. 云南水力发电，2008，24(3)：32-36.

Pan Changyong，Chai Yusong. Study on junction structure between gravity dam and earth-rockfill dam of Guanyinyan hydropower station[J]. Yunnan Water Power，2008，24(3)：32-36(in Chinese).

［4］ Goodman R E，Taylor R E，Brekke T. A model for the mechanics of jointed rock[J]. Journal of Soil Mechanics and Foundation Division，ASCE，1968， 94(3)：637-659.

［5］ Desai C S，Zaman M M，Lightner J G，et al. Thin-layer element for interfaces and joints[J]. International Journal for Numerical and Analytical Methods in Geomechanics，1984，8：19-43.

［6］ 殷宗泽，朱 泓，许国华. 土与结构材料接触面的变形及数学模拟[J]. 岩土工程学报，1994，16(3)：14-22.

Yin Zongze，Zhu Hong，Xu Guohua. Numerical simulation of the deformation in the interface between soil and structural material[J]. Chinese Journal of Geotechnical Engineering，1994，16(3)：14-22(in Chinese).

［7］ Bandis S C，Lumsden A C，Barton N R. Fundamentals of rock joint deformation[J]. International Journal of Rock Mechanics and Mining Sciences，1983，20(6)：249-268.

［8］ 朱伯芳. 有限单元法原理与应用[M]. 北京：中国水利水电出版社，1998.

Zhu Bofang. The Finite Element Method Principle and Application [M]. Beijing：China Water Power Press，1998(in Chinese).

［9］ Clough G W，Duncan J M. Finite element analysis of retaining wall behavior[J]. Journal of Soil Mechanics and Foundation Engineering Division，ASCE，1971，97(12)：1657-1673.

［10］ Duncan J M，Zhang C Y. Nonlinear analysis of stress and strain in soils[J]. Journal of Soil Mechanics and Foundation Division，1970，96(SM5)：1629-1653.

［11］ 顾淦臣. 土石坝地震工程[M]. 南京：河海大学出版社，1989.

Gu Ganchen. Earthquake Engineering of Earth and Rockfill Dams[M]. Nanjing：Hehai University Press，1989(in Chinese).

［12］ Serff N，Seed H B，Makdisi F I，et al. Earthquake Induced Deformation of Earth Dams[R]. EERC-76-4. Berkeley：Earthquake Engineering Research Center，University of California，1976.