用Catmull-Clark细分及网格调整方法重构牙齿曲面

王玉慧， 张玉茹

（北京航空航天大学机械工程及自动化学院，北京 100191）

用Catmull-Clark细分及网格调整方法重构牙齿曲面

王玉慧， 张玉茹

（北京航空航天大学机械工程及自动化学院，北京 100191）

首先根据牙齿表面测量数据点，计算出其长方体包围盒；并据此构造细分曲面的初始网格；采用矩阵对角化方法，推导Catmull-Clark细分极限点的表达式，计算初始网格的顶点经过细分后的极限点；按照极限点逼近数据点的原则移动控制网格顶点，经过逐次再细分、再调整网格，使各级网格在数据点的“引导”下逐步变形，使网格逐步逼近牙齿表面的测量数据点集合，实现牙齿表面模型的三维重建。

计算机辅助几何设计；曲面重构；细分造型；牙齿模型

在虚拟现实环境中，虚拟场景建模是一项重要工作，直接影响系统的性能。本文研究力觉交互虚拟现实牙科手术培训中由测量数据点重构牙齿表面模型。

关于牙齿表面的重构，LI Zhong[1]采用双三次贝塞尔曲面进行了牙齿表面模型的重构，针对每一条轮廓线，用若干三次贝塞尔曲线段拼接得到；然后再对不同轮廓上的对应点进行贝塞尔曲线插值，得到由G2连续的双三次贝塞尔曲面片拼接而成的表面模型。文献[2]采用B-样条曲面进行牙齿表面曲面模型的重构，由于B-样条反算要解较大的线性方程组，计算量较大。Mikrogeorgis G[3]利用人类第六颗牙齿的断层图像得到断层轮廓数据点，通过人机交互的方式进行基于三角片的牙齿表面模型重构。Isaac Newton Lima da Silva[4]由牙齿的断层扫描图像得到牙齿的断层数据点，然后构建牙齿的多面体模型，再利用商用软件Pro/E得到牙齿的实体模型。

用曲面拟合进行物体表面模型的重构计算复杂、计算量较大；采用直接给物体表面的数据点建立拓扑关系的方法，所建立的物体表面模型的质量依赖于测量数据点的测量精度及数据点的分布情况。本文尝试采用细分造型构建牙齿表面模型。

细分方法是通过将多边形网格中的每个多边形按照一定的规则分成几个子多边形，从而得到更光滑的网格。其算法简单、直观，适用于构造复杂曲面，Chaikin[5]于 1974年提出了通过重复割去多边形的角，最终得到光滑的极限曲线的方法，后来被证明该极限曲线是以多边形为控制多边形的二次 B-样条曲线。Catmull和 Clark[6]提出基于四边形的细分方法，其细分极限曲面是双三次 B-样条曲面，文中指出曲面在规则点处（关联边数为4）能达到曲率连续，而在异常点处曲面是切线连续。Doo D, Sabin[7]采用离散付立叶变换的方法证明了Catmull和Clark的结论。A A Ball[8-9]分别采用矩阵的特征值性质和离散付立叶变换的方法证明了以上结论。Loop[10]提出了一种基于三角形网格的细分方法，较之基于四边形网格的细分方法算法更简单。Suzuki[11]提出了一种基于 loop细分和网格调整的曲面重构算法。本文采用 Catmull-Clark细分方法，并针对数据点有噪声，利用改进的网格调整方法进行牙齿曲面的三维重构，力图使重构的网格在逼近牙齿数据点的同时具有较好的光顺性。

1 算法原理

1.1 Catmull-Clark细分极限点表达式

由文献[9]，经过 Catmull-Clark计算细分后新的点点、边点和面点的公式为

图1 Catmull-Clark细分算法示意图

求得矩阵的特征值和特征向量如表1所示。

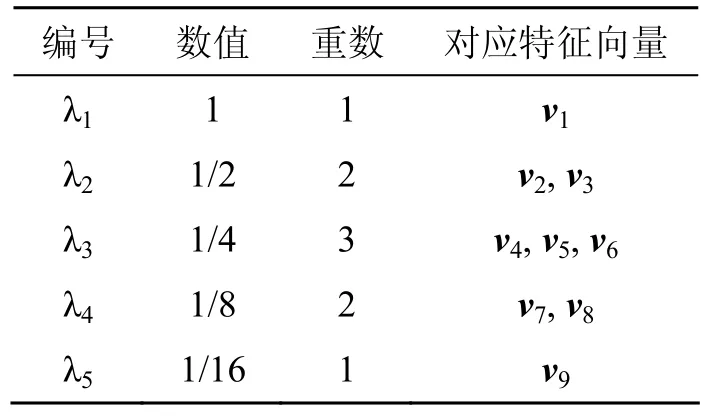
表1 矩阵的特征值和特征向量

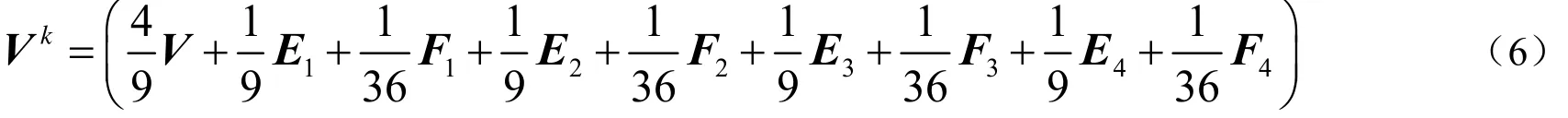
采用与n=4时同样的求细分极限点的方法求得，当n=3时

1.2 细分网格的构造与调整

首先，计算牙齿表面数据点的包围盒，将包围盒略作放大，然后建立如图2左所示的初始网格；对初始网格进行一次 Catmull-Clark细分得到图2右所示的网格；然后用式(3)、式(4)求出网格上每个顶点的细分极限点。

设牙齿数据点集合为 Pi(i = 0 ,1,… ,s )，网格顶点集合为 Vi(i = 0 ,1,… ,m)，其细分极限点集为( i = 0 ,1,… ,m)，其中 m为数据点个数。针对 n =4和 n =3两种情况，用式(6)和式(7)计算每一个极限点。再对于每一个极限点，在数据点集合中求出与它距离最近的点 Pj。

δi则表示 Vi的对应细分极限点与其最近数据点 Pj之间的向量差。

则网格中所有顶点距离其最近数据点的平均距离为

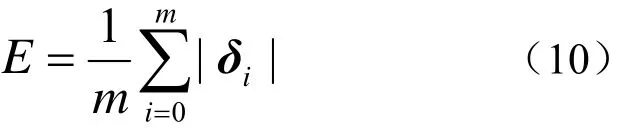
接下来进行网格调整，调整的原则是移动控制网格顶点V使得其所对应的新的细分极限点V∞'重合于其在牙齿表面数据点中的最近距离点。

如果要根据牙齿表面数据点按照网格顶点的调整原则计算出所有新的控制顶点V，则需要解庞大的线性方程组，本文参考[11]的方法，用每次仅移动V而不改变iE，iF进行迭代的方法，即，在考虑使得 'V 对应的细分极限点逼近数据点时，只移动V，而不考虑其周围的关联点。等到一个点作为V移动完毕后，再更换一个点作为V，这时就仅考虑当前V点的移动。通过逐次迭代，使得调整后的网格点对应的细分极限点逐步接近其对应的最近点，直到满足距离误差ε＜E为止。

根据网格顶点的调整原则，原则上应使得细分的极限点重合于牙齿表面数据点中距其最近的数据点，即使得

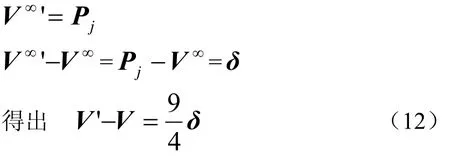
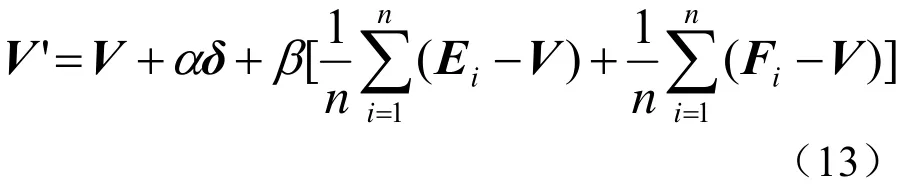
其中 α为细分极限点逼近牙齿表面数据点逼近项的系数；β为反映网格调整过程中，当一个控制网格上的顶点被调整过程中，其周围的点对该点的制约因素。这两个参数的选取视具体应用问题的要求，通过实验选定。

调整网格控制顶点算法步骤如下：

（1） 根据牙齿表面测量数据点建立初始网格；

（2） 分别用式(6)和式(7)计算网格中 4=n和 3=n 的每个控制顶点的 Catmull-Clark细分极限点；

（3） 求出牙齿表面测量数据点中距离每个极限点最近的点；

（4） 由式(9)计算网格上某一顶点的细分极限点与其最近数据点的距离；

（5） 由式(10)计算网格上所有点的细分极限点到其最近数据点的平均距离；

（6） 设定误差阈值ε，如果ε＜E，则不再调整网格；

（7） 如果ε＞E，则对于网格中所有顶点用式(13)计算网格顶点V经过一次移动后的新位置 'V，将V移动到 'V；

（8） 将调整后的网格进行一次 Catmull-Clark细分；

（9） 用细分得到的新网格代替上一级网格，然后重复(2)～(9)的过程。

2 实验结果

图2 网格建立及调整过程

表2 初始网格参数

将初始网格进行一次调整后的网格如图2(b)所示，调整后再细分一次的网格如图2(c)所示，在此基础上再次调整后的网格如图2(d)所示，图2(e)、图 2(f)分别为第二次调整网格后再进行一次、二次细分后的网格。图2(g)为牙齿模型的渲染图。

图3 平均误差与迭代次数的关系

3 结 论

本文把细分算法应用于力觉交互的虚拟现实牙科医生手术培训系统的虚拟场景建模中，构造出牙齿曲面的不同精确程度的网格，并且针对原始数据点云有噪声的问题，在网格调整中加入了光顺项使得构造的牙齿表面网格在满足精度要求的同时具备一定的光顺性。且细分算法简单，易于实现。

[1]LI Zhong, MA Li-zhuang, TAN Wu-zheng, et al.Reconstruction from contour lines based on bi-cubic Bézier spline surface [J]. Journal of Zhejiang University SCIENCE A, 2006, 7(7)：1241-1246.

[2]吴 雯. 人工牙的三维重建及其交互实现[D]. 北京：中国科学院, 2000.

[3]Mikrogeorgis G, Lyroudia K L, Nikopoulos N, et al.3D computer-aided reconstruction of six teeth with morphological abnormalities [J]. International Endodontic Journal, 1999, 32(2)：88-93.

[4]Isaac Newton Lima da Silva, Gustavo Frainer Barbosa,Rodrigo Borowski Grecco Soares, et al. Creating three-dimensional tooth models from tomographic images [J]. Stomatologija, Baltic Dental and Maxillofacial Journal, 2008, (10)：67-71.

[5]Chaikin G. An algorithm for high speed curve generation [J]. Computer Graphics and Image Processing, 1974, (3)：346-349.

[6]Catmull E, Clark J. Recursively generated B-spline surfaces on arbitrary topological surfaces [J].Computer-Aided Design, 1978, 10(6)：350-355.

[7]Doo D, Sabin M. Behaviour of recursive division surfaces near extraordinary points [J].Computer-Aided Design, 1978, 10(6) ：356-360.

[8]Ball A A, Storry D J T. Conditions for tangent plane continuity over recursively generated B-spline surfaces [J].ACM Trans. Graph., 1988, 7(2)：83-102.

[9]Ball A A, Storry D J T. A matrix approach to the analysis of recursively generated B-spline surfaces [J].Computer-Aided Design, 1986, 18(8)：437-442.

[10]Charles Teorell Loop. Smooth subdivision surfaces based on triangles [D]. Master's thesis, University of Utah, Department of Mathematics, 1987.

[11]Hiromasa Suzuki, Shingo Takeuchi, Fumihiko Kimura,et al. Subdivision surface fitting to a range of points[C]//Proceedings of the 7th Pacific Conference on Computer Graphics and Applications. Seoul Korea, 1999：158-167.

Tooth Surface Reconstruction by Catmull-Clark Subdivision and Mesh Modification

WANG Yu-hui, ZHANG Yu-ru
( School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics, Beijing 100191, China )

Bounding box of data points are obtained according to data points of tooth surface, based on which initial control meshes are constructed. The limit points of Catmull-Clark subdivision are calculated by the expression derived by means of matrix diagonalization. Vertexes of control mesh are moved in order that each limit point approximates to its data point. Then subdivision and modification of the meshes are applied repeatedly so that the mesh at each level becomes deformed gradually under the “guide” of points to approximate to data points of tooth surface. Thus the three-dimensional reconstruction of tooth model is achieved.

computer aided geometric design; surface reconstruction; subdivision; tooth model

TP 391

A

1003-0158(2010)06-0056-06

2009-04-15

王玉慧（1964-），女，河南郑州人，副教授，博士，主要研究方向为计算机图形图像处理。