双视三维重建的高精度运动参数估计方法
蔡 涛, 段善旭, 李德华
(1. 华中科技大学电气与电子工程学院,湖北 武汉 430074;2. 华中科技大学图像识别与人工智能研究所图像信息处理与智能控制教育部重点实验室,湖北 武汉 430074)
双视三维重建的高精度运动参数估计方法
蔡 涛1, 段善旭1, 李德华2
(1. 华中科技大学电气与电子工程学院,湖北 武汉 430074;2. 华中科技大学图像识别与人工智能研究所图像信息处理与智能控制教育部重点实验室,湖北 武汉 430074)
从两幅透视图像恢复被摄目标的三维结构是计算机视觉最基本的任务之一,其中,运动估计算法的性能决定了最终的三维重建精度。首先讨论了双视成像的基本数学模型,并介绍了几种现有运动参数估计方法的基本原理和不足。随后,基于投影误差最小判决函数,提出了用于双像运动估计的改进非线性迭代优化方法。数值仿真结果表明,在大平移小旋转角及小平移大旋转角2种运动条件下,采用文中提出的方法,运动估计精度均有所提高。此外,根据运动参数的估计值对真实目标进行三维重建实验,结果表明尺度重建误差小于2%且角度误差在3°以内。
计算机视觉;三维重建;运动参数估计;Levenberg-marquard优化算法
空间3D目标的运动估计和几何重建是计算机视觉和虚拟现实中的重要研究内容[1]。随着光学器件及数字信号处理技术的不断提高,高性能的消费类数码相机日益普及,使得非专业人员进行计算机视觉的应用研究成为可能。然而,不同于标准双摄像机立体视觉系统[2],通常条件下只有单个数码相机可以利用,为此需要在两个视角获取同一目标的2幅透视视图[3]。此时摄像机的相对运动参数估计算法的性能对后续的3D重建或测量的精度起着决定性的因素。经典的线性算法,如两步估计法[4]、奇异值分解法[5]等,具有简单、快速的优点,但是对图像噪声极其敏感,导致后续重建精度不够理想。为改善运动参数的估计精度,本文在Horn的迭代优化方法[6]基础上提出了改进的参数优化判决函数,并采用Levenberg-Marquard非线性优化方法获得了高精度的运动估计结果。仿真和实验结果表明,本文方法非常适合基于数码相机的低成本视觉系统。
1 双视成像模型
若已获得某刚性目标的两幅透视投影图像,计算机视觉的一般任务就是确定两幅图像间的对应关系并由此估计目标的3D几何结构。总的来讲,摄像机与目标间存在3种配置情况:① 单摄像机从不同角度拍摄静止目标获得2幅图像,需确定摄像机相对运动参数及目标3D结构;②单个固定摄像机在不同时刻拍摄运动目标获得2幅图像,需确定目标的运动参数及其3D结构;③ 2个摄像机在同一时刻获取静止目标的 2幅图像,需确定2摄像机的相对位姿及目标3D结构。

图1 双视成像模型
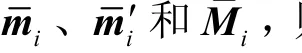
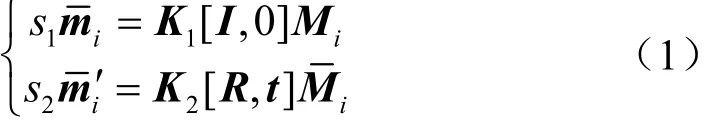
式中 K1和K2分别是两个摄像机的内参数矩阵,s1和s2是常数因子。经过变换和整理可消掉s1、s2和,得[1]

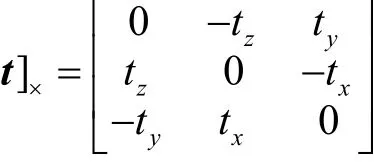
式(2)可改写为所谓的极线方程


其中 E=[t]×R=t×R 即所谓本质矩阵(Essential Matrix)。易知,F矩阵和E矩阵的转换关系为

式中的等号在相差一个比例因子意义下成立。在得出摄像机的相对位姿及内部参数后,就可以在相差某个常数因子的条件下实现物体的3D欧氏重建。
2 算法描述
2.1 运动参数的初值计算
前已说明:若摄像机的内参数已经标定,则从F矩阵可以得到E矩阵,其包含了两摄像机间的运动关系,即平移向量和旋转矩阵。为求取这两个值,Maybank和Faugeras[5]在研究双像运动估计问题时给出并证明了下列定理:
定理1 实数3阶矩阵E能够分解成一个反对称矩阵T和一个旋转矩阵R的乘积E=TR,当且仅当它有一个奇异值为零,另两个奇异值相等。
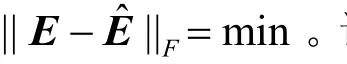
为确定T和R的符号,可选取一对图像匹配点数据作为测试点,在4种符号配置条件下分别计算该点的3D位置,由此确定该3D点在两摄像机中的深度,选择在两个摄像机中深度均为正值的R和t,即为正确解。
2.2 改进的迭代优化
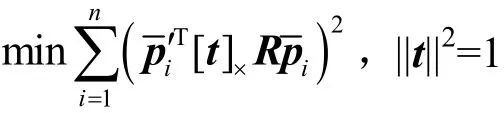

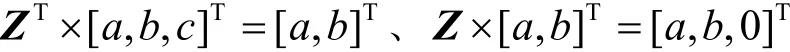

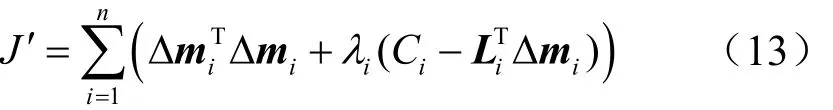
令J′关于iΔm的偏导数为O,于是有
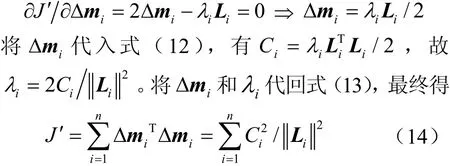
引入拉格朗日乘子 λ,将约束优化问题(10)转变为最小化下式实际上

为了最小化准则函数(15),本文采用Levenberg-Marquard非线性优化方法[8]。需要注意的是,E=[t]×R包含5个自由参数,其中旋转角 R有 3个(3维旋转向量)、单位平移向量 t有 2个(单位球面坐标),故整个优化过程在 5维参数空间内进行。
3 性能比较和分析
3.1 运动估计仿真实验

实验1 t=[500, 0, 0]T、r对应欧拉角为[10°,10°, 0°]T,代表大平移小旋转角情况,实验结果如图2(a)、图2(b)所示。
实验2 t=[100, 0, 0]T、r对应欧拉角为[60°,10°, 0°]T,代表小平移大旋转角情况,实验结果如图2(c)、图2(d)所示。
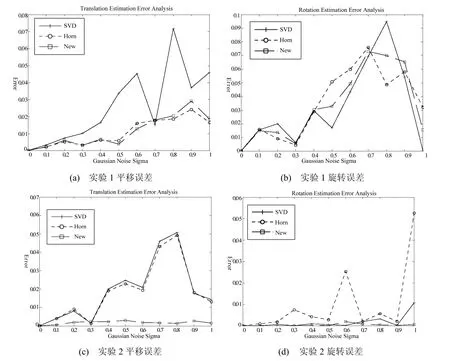
图2 运动参数估计误差分析
从实验中可以发现 SVD法的结果最差,而使用Horn迭代优化方法后运动参数的误差都有所改善,特别是对平移估计的改善较为显著。但是,Horn迭代对于旋转量改善不多,在某些情况下甚至会变差(如图 2(b)),这一现象也说明了最小化准则式(6)并不是最优的。相比之下,使用最优准则式(9)的本文方法,在 2中条件下平移和旋转参数的估计都能够得到改进。
3.2 3D重建实验
为评估本文方法改善双目视觉3D重建精度的能力,分别对模拟3D目标和真实3D目标进行了运动估计和3D重建实验。
3.2.1 模拟3D目标重建
选取的模拟摄像机参数同3.1节,观测目标为模拟的摄像机定标物,如图 3(a),其中两块板夹角90°,每块大小为200×400单位,其重心距离第一个摄像机光心600单位。摄像机相对运动参数 t =[-40, 0, 0]T,r =[0, 0, π/10]T,图像点叠加σ=0.5高斯噪声。图3(b)和图3(c)分别是模拟目标在左、右摄像机上的成像。
分别采用 SVD、Horn迭代以及本文方法估计运动参数并使用迭代最小二乘三角测量方法[10]重建每个空间点的3D坐标。随后将重建3D点分别反投影到2个摄像机平面上计算重投影误差。表1中列出了运动参数估计结果以及重投影误差均方根。从中可以发现一个比较有趣的现象,那就是真实结构的重投影误差居然比改进的优化方法还大,这可能与使用的重投影误差最小准则有关,具体原因有待进一步研究。

表1 模拟3D目标重建实验结果
3.2.2 真实3D目标图像重建
这里,实验所使用的图像输入设备是UnisDC-Q8数码相机。采集图像时,相机处于手动调焦状态并始终保持不变。图像原始分辨率为1600×1200,降采样成为800×600。采用文献[11]中的方法定标,后得到内部参数为:主点u0=357.1、v0=347.1、焦距au=2101.8、av=2113.5。重建过程中忽略镜头的畸变效应。
重建的目标为UnisDC-Q8的包装盒。图4(a)显示的是采集的两幅图像以及使用改进Harris角点检测算法[12]提取到的特征点。使用三角测量方法重建得到3D散乱点云,其俯视图如图4(c)而左视图如图4(d)。将最终的三维点集三角化、计算每个特征点的纹理坐标生成 VRML文件,其显示效果如图4(d)。
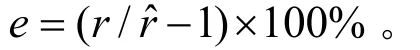

表3 矩形ABCD的内角重建值
4 结 论
提出了一种用于双像三维重建的改进运动参数估计算法。该算法首先从基础矩阵和摄像机的内参数矩阵估计本质矩阵,然后采用奇异值分解方法获得旋转矩阵和平移向量的初始估计,最后通过对投影误差目标函数进行 L-M 非线性迭代优化对运动参数进行求精。实验结果表明,该算法计算精度高,极大的改善了后续的3D重建精度,即便是手工选取匹配点,尺度重建误差仍低于2%、角度重建误差在3°以内。因此,该算法非常适合基于简易摄像设备的3D测量及目标3D重建。
[1]马颂德, 张正友. 计算机视觉——计算理论与算法基础[M]. 北京:科学出版社, 1998. 72-116.
[2]Dhond U R, Aggarwal J K. Structure from stereo–a review [J]. IEEE Transactions on Systems, Man and Cybernetics, 1989, 19(6):1489-1510.
[3]Longuet-Higgins H C. A computer algorithm for reconstructing a scene from two projections [J].Nature, 1981, 293:133-135.
[4]Weng J, Huang T S, Ahuja N. Motion and structure from two perspective views:algorithms, error analysis,and error estimation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(5):451-476.
[5]Faugeras O, Maybank S. Motion from point matches:multiplicity of solutions [J]. International Journal of Computer Vision, 1990, 4(3):225-246.
[6]Horn B K P. Relative orientation [J]. International Journal of Computer Vision, 1990, 4(1):59-78.
[7]Zhang Zhengyou. A new multistage approach to motion and structure estimation:from essential parameters to euclidean motion via fundamental matrix [R]. Research Report 2910, INRIA Sophia-Antipolis, France, 1996.
[8]MathWorks. Optimization toolbox for use with matlab,matlab user’s guide, version 2.0 [M]. The Math Works,Inc. 2001. 2-24.
[9]Hartley R I. In defence of the 8-point algorithm [C]//Proceedings of the 5th Proc. International Conference on Computer Vision. IEEE Computer Society Press,Boston, MA, 1995:1064-1070.
[10]Richard I Hartley, Peter Sturm. Triangulation [J].Computer Vision and Image Understanding, 1997,68(2):146-157.
[11]Zhang Zhengyou. A flexible camera calibration by viewing a plane from unknown orientations [C]//Proceedings of the 7th International Conference on Computer Vision, 1999:666-673.
[12]Harris C, Stephens M. A combined corner and edge detector [C]//Proceedings of the 4th Alvey Vision Conference, 1988:147-151.
High Accuracy Motion Estimation Method Used for Three Dimensional Reconstructing from Two Views
CAI Tao1, DUAN Shan-xu1, LI De-hua2
( 1. College of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan Hubei 430074, China;2. Institute for Pattern Recognition and Artificial Intelligence, State Education Commission Key Laboratory for Image Processing and Intelligent Control, Huazhong University of Science and Technology, Wuhan Hubei 430074, China )
Recovering the 3D geometric structure of an observed object from its two perspective views is one of the most important tasks in the computer vision research. It’s well known that the accuracy of 3D reconstruction is mainly decided by the performance of motion estimation method. In the paper, the fundamental model of two-view imaging system is introduced and the principles and disadvantages of some motion estimation methods are analyzed. To improve the estimation accuracy, a modified non-linear iterative optimization method is proposed based on the projective error minimization. The numerical simulations prove that the estimation accuracy is improved either under large translation and small rotation or under small translation and large rotation. Furthermore, the proposed method is verified by reconstruction from two view images of simulated object and real object. The result shows that the metric error is below 2% and the angle error below 3°.
computer vision; 3D reconstruction; motion estimation; Levenberg-marquard algorithm
TP 391
A
1003-0158(2010)06-0023-06
2009-03-03
国家自然科学基金资助项目(50737004/E0706)
蔡 涛(1974-),男,湖北武汉人,讲师,博士,主要研究方向为信息检测技术与计算机视觉。

