代数三角混合Bézier型插值曲线

苏本跃， 盛 敏,

（1. 安庆师范学院计算机与信息学院，安徽 安庆 246011；2. 合肥工业大学计算机与信息学院，安徽 合肥 230009）

代数三角混合Bézier型插值曲线

苏本跃1， 盛 敏1,2

（1. 安庆师范学院计算机与信息学院，安徽 安庆 246011；2. 合肥工业大学计算机与信息学院，安徽 合肥 230009）

通过一类代数三角混合Bézier型基函数的定义，构造了一类C2连续的代数三角混合Bézier型插值曲线。该曲线继承了Bézier曲线的一些优良特性，并能充分克服Bézier型基函数不能精确表示二次曲线曲面以及某些超越曲线曲面的弱点。另外，利用形状控制参数可以灵活调节曲线形状，进一步增强了曲线曲面的表现能力。最后实例表明了新的插值曲线应用于几何造型的有效性。

代数三角混合多项式；Bézier型曲线；曲线插值；形状参数

在计算机辅助设计(CAD)领域，用代数三角混合多项式来表示参数曲线曲面是近年来出现的一类比较崭新的自由曲线曲面造型方法，目前已经成为 CAGD领域研究的一个新热点。张纪文[1]在空间Span{1, t, cost, sint}上提出了均匀节点的C-曲线概念。2001年，Mainar等[2]在代数三角混合函数空间中提出了规范B基的构造。汪国昭等[3-5]在扩展的代数三角混合函数空间中提出了k阶代数三角多项式样条。Han，吴晓勤，苏本跃等[6-9]在三角函数空间定义了一类 Bézier型曲线，使其具有Bézier曲线的类似性质，同时又具有三角函数的若干优点。

上述代数三角混合样条曲线的特点是：①样条基函数是由代数多项式函数与三角多项式函数混合构造而成，故由此构造的代数三角混合样条曲线一方面继承了多项式样条曲线的特点，另一方面可以克服工业产品外形设计中某些曲线不能用多项式基函数精确表示的缺点；② 样条基函数的参数定义区间由形状参数α控制，是可变的。当形状参数α发生变化时，代数三角混合样条曲线形状也发生相应的改变。然而，形状参数α又决定了定义区间的大小，在产品设计过程中往往需要重新参数化；并且随着形状参数α的改变，曲线只能从单边逼近同阶的 Bézier曲线。

然而，上述曲线造型方法是逼近型的，在构造插值型曲线时显得较为复杂，本文通过一类代数三角混合 Bézier型曲线的定义，构造了一类C2连续的代数三角混合Bézier型插值曲线。一方面继承了Bézier插值曲线的特性，另一方面可以充分克服 Bézier基函数不能精确表示二次曲线及某些超越曲线曲面的弱点，以此进一步加强插值型曲线曲面的表现能力。

1 代数三角混合Bézier型曲线曲面

1.1 代数三角混合Bernstein型基函数的定义

若令参数t的定义区间为[0, π/2]，在由多项式函数与三角函数构成的混合函数空间{1, t, sint,cost, …, sinkt, coskt}以及{1, t, t2, sint, cost, …,sinkt, coskt}中可构造与 Bernstein基函数的性质相类似的拟 Bernstein型基函数。由于现有的造型曲线几乎均定义在区间[0, 1]上，故定义拟三次Bernstein型基函数如下：

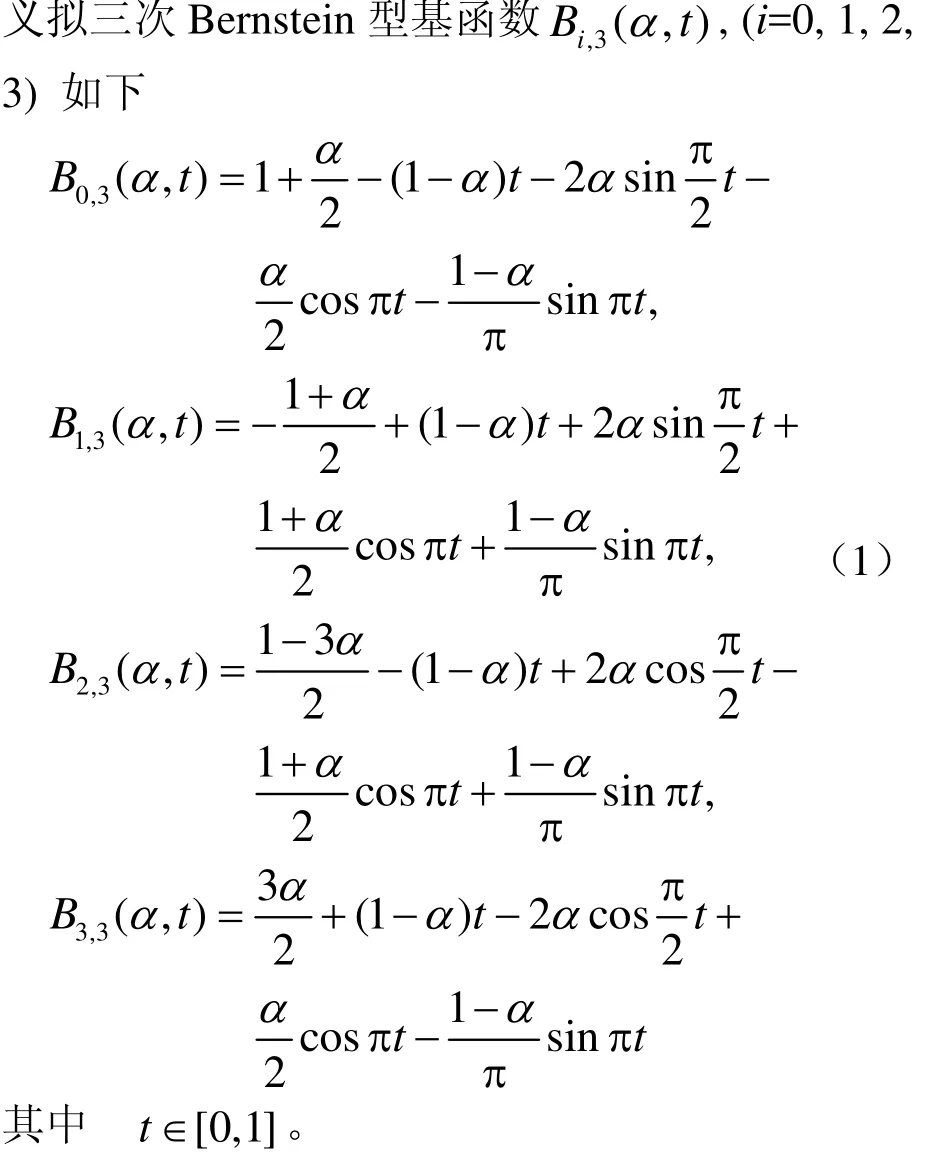
1.2 Bernstein型代数三角混合多项式基函数的性质

以上构造的拟三次 Bernstein型基函数Bi,3(t)具有Bernstein基函数类似性质：

性质1 拟三次Bernstein型基函数具有非负性，即

性质2 拟三次Bernstein型基函数具有以下端点性质

性质3 拟三次Bernstein型基函数具有对称性，即

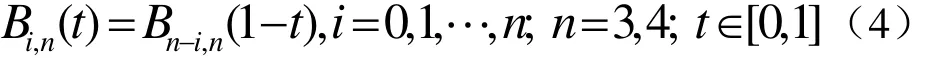
性质 4 拟三次 Bernstein型基函数具有权性，即

注：性质1～4可由拟三次Bernstein型基函数定义直接推出。并且由式(2)及式(5)知，拟三次Bernstein型基函数同样具有单位剖分性。

1.3 代数三角混合Bézier型曲线

定义2 设给定四个控制顶点 q0, q1, q2,q3，以及任取实数α, α ∈ [ 0,1]，则可定义一条带有形状控制参数的代数三角混合Bézier型曲线

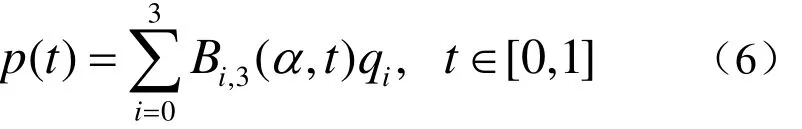
其中 Bi,3(α,t), i =0,1,2,3为拟三次Bernstein型基函数，如图1所示。

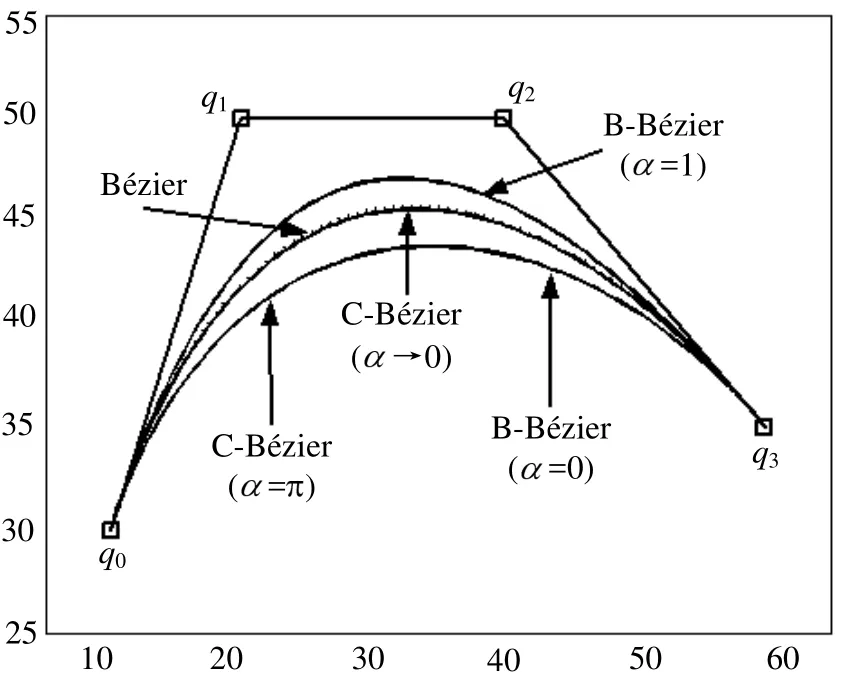
图1 代数三角混合Bézier型曲线

令 k (α) = 2 (1 - α ) + πα , m =π2/4，则由性质2容易推得拟三次Bézier型曲线具有以下端点性质

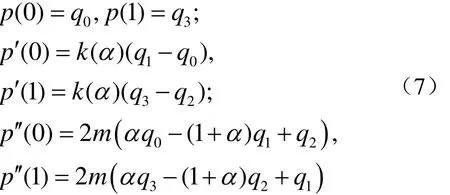
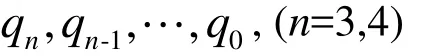
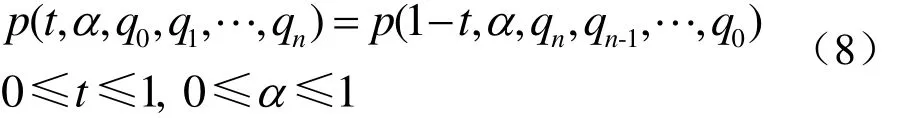
同时拟 Bézier型曲线的形状与坐标轴的选取无关，而且由拟 Bernstein型基函数的单位分解性知，整条 Bézier型曲线位于由控制顶点q0, q1,… ,qn张成的控制多边形的凸包中。

2 代数三角混合Bézier型插值曲线

定义3 给定[a,b]上连续函数f在已知分割

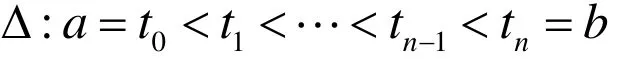
上的值为 f ( ti),i = 0 ,1,… ,n , 若分段代数三角混合Bézier型曲线p(t)满足下列条件：

（1） p(t)为定义 2表示的代数三角混合Bézier型曲线，且在子区间[ti, ti+1]上表示为pi(t),则称 p(t)为 C2连续的分段代数三角混合 Bézier型插值曲线。

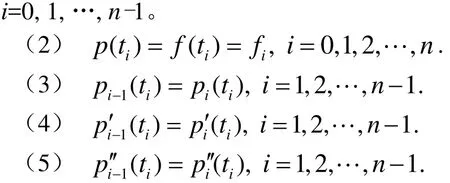
由定义3分段代数三角混合Bézier型插值曲线p(t)可改写为

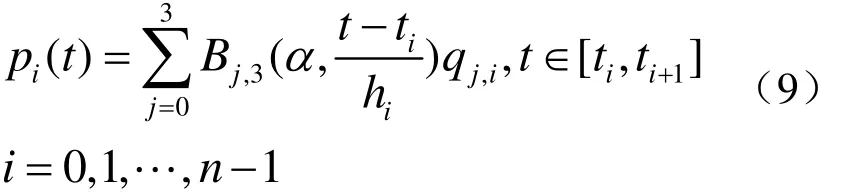
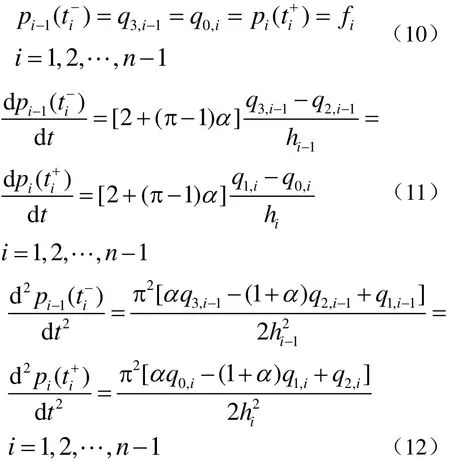
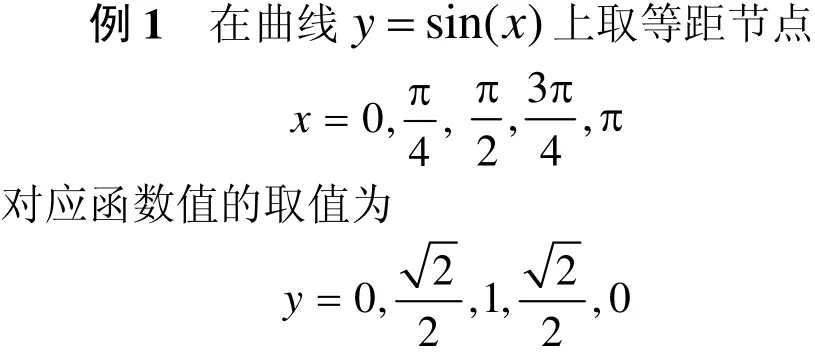
由分段代数三角混合Bézier型插值曲线的定义，在区间[a, b]上n-1个内节点 t1, t2, … ,tn-1处应满足则插值该5个数据点的代数三角混合Bézier型插值曲线如图2所示。并且由图2可知，不改变曲线的 C2连续性，调节控制参数α可以提高插值曲线逼近阶。

图2 给定型值点的代数三角混合Bézier型插值曲线

3 结 论

本文通过一类代数三角混合 Bézier型曲线的定义提出了相应的插值算法。具有下列优点：首先，它继承了相应的Bézier曲线的基本性质，如端点性质、对称性、几何不变性、凸包性等以及三次样条的 C2连续性等。其次，提供了一个形状控制参数，用户除了利用控制顶点调节曲线曲面形状外，还可以通过形状控制参数调整曲线曲面形状，增强了曲线曲面形状调整的灵活性。而且在几何连续性的意义下，曲线曲面形状的调整既可以局部调整又可以全局调整。第三，利用局部控制参数调节曲线形状使得曲线变化的范围更大，选取合适的控制参数可以使曲线从两边逼近同阶的Bézier曲线及B样条曲线。最后，选取合适的形状控制参数以及合适的控制顶点，本文提出的 Bézier型代数三角混合多项式曲线可精确表示一些常用的圆锥曲线和心脏线、摆线、螺旋线等超越曲线。 这使得工程师在CAD造型设计以及数控加工中，可以只需要选取很少的曲面片就可以精确表示用户所需要的某些特殊曲面造型，而不需要像传统多项式方法一样需要多片曲面片的拼接以达到用户满意的精度。由此可大大提高曲线曲面的生成效率和表示精度。

[1]ZHANG J W, KRAUSE F L. Extending cubic uniform B-splines by unified trigonometric and hyperbolic basis [J]. Graphic Models, 2005, 67：100-119.

[2]MAINAR E, PEÑA J M. A basis of C-Bézier splines with optimal properties [J]. Computer Aided Geometric Design, 2002, 19：291-295.

[3]WANG G Z, LI Y J. Optimal properties of the uniform algebraic trigonometric B-splines [J]. Computer Aided Geometric Design, 2006, 23：226-238.

[4]HOFFMANN M, LI Y J, WANG G Z. Paths of C-Bézier and C-B-spline curves [J]. Computer Aided Geometric Design, 2006, 23：463-475.

[5]WANG G Z, CHEN Q Y, ZHOU M H. NUAT B-spline curves [J]. Computer Aided Geometric Design, 2004, 21：193-205.

[6]HAN X L. Cubic trigonometric polynomial curves with a shape parameter [J]. Computer Aided Geometric Design, 2004, 21：535-548.

[7]苏本跃, 黄有度. 一类Bézier型的三角多项式曲线[J].高等学校计算数学学报, 2005, 27(3)：202-208.

[8]SU B Y, TAN J Q. A family of quasi-cubic blended splines and applications [J]. J. Zhejiang Univ.SCIENCE A, 2006, 7(9)：1550-1560.

[9]吴晓勤, 韩旭里, 罗善明. 带形状参数的二次三角Bézier曲线[J]. 工程图学学报, 2008, 29(1)：82-87.

Algebraic Trigonometric Blending Bézier-type Interpolation Curves

SU Ben-yue1, SHENG Min1,2
( 1. School of Computer and Information, Anqing Teachers College, Anqing Anhui 246011, China;2. School of Computer and Information, Hefei University of Technology, Hefei Anhui 230009, China)

A class of C2continuous algebraic trigonometric blending Bézier-type interpolation curves is constructed based on the definition of free form algebraic trigonometric blending Bézier-type curves. The introduced curves inherit some characteristics which the Bézier interpolation curves have. Meanwhile, the new curves can accurately represent some conic and transcendental curves, which are more powerful than the Bézier interpolation curves. Moreover,the shapes of curves can be adjusted freely by an introduced control parameter in the base functions. At last, the illustrations show that the new interpolating curves are effective in practice on geometric modeling.

algebraic trigonometric blending polynomial; Bézier-type curve; curve interpolation; shape parameter

TP 391.72; O 241.3

A

1003-0158(2010)06-0039-06

2009-02-24

国家自然科学基金资助项目（60773128）；安徽省教育厅自然科学研究资助项目（KJ2009A123）；安徽省高等学校优秀青年人才基金资助项目（2009SQRZ156）

苏本跃（1971-），男，安徽芜湖人，副教授，博士，主要研究方向为计算机图形学，数字图像处理，科学与工程计算。

book=44,ebook=81