改进变论域模糊控制及其在混沌系统中的应用

路永坤，夏超英

(1. 天津大学电气与自动化工程学院，天津 300072；2. 天津科技大学自动化学院，天津 300222)

变论域自适应模糊控制器[1-4]根据跟踪误差的大小，来改变模糊论域的伸缩因子．在模糊规则形式不变的情况下，论域变小，相当于增加模糊规则．反之，相当于减少模糊规则．

文献[4]中给出了一种基于观测器的鲁棒自适应变论域模糊控制．但其稳定设计未考虑反馈增益向量对观测器估计误差的影响，所以稳定设计需要进一步改进．

从模糊系统逼近误差角度看，文献[5]中模糊系统的前件(条件)部分的隶属度函数固定，是其模糊逼近误差产生的一个主要原因．但在文献[1-4]中，仅是一种针对论域的比例改变．而模糊系统隶属度函数的中心和宽度的相对关系，尤其是前件隶属度函数，则具有非线性特点，对模糊逼近误差的影响更大．为了进一步减小模糊逼近误差，原模糊系统结构中的非线性因素也需要能被在线调整．

文献[4]中不确定项包含模糊逼近误差以及外部扰动．而鲁棒控制项表达式中需要知道不确定项的界．若不确定项的界不易获得，由此设计的鲁棒控制项过小时，起不到应有的补偿效果；而鲁棒控制项过大的，又容易引起输入控制信号抖振[6]．为了减小鲁棒控制项的设计难度，在变论域模糊控制器中，需要设计一种可以在线动态减小最小模糊逼近误差的算法．

在文献[7]中利用级数展开式，得到了关于模糊基函数的宽度和中心的线性展开式，并由此推出模糊系统隶属度函数的宽度和中心都可在线调整的自适应律．但这种级数展开式仍含有非线性部分，其中的非线性因素仍然是模糊系统逼近误差的主要来源．虽然文献[7]中亦探讨了模糊系统动态结构的问题，但其中动态增加的新模糊规则中隶属度函数宽度以及输出权重缺乏设计依据．这种设计难免因为新加入的规则，使得系统稳定性变差．

在文献[8]中，提出一种自组织结构算法．但其中有关减规则和替换规则的方法，基于“当前”的控制情况，对整个模糊系统结构缺乏考虑，也需要进一步改进．

基于上述问题，笔者提出一种在线自组织结构算法，并运用到改进的基于观测器的鲁棒自适应变论域模糊控制器中．

1 改进变论域模糊控制算法

1.1 改进稳定设计

考虑单输入单输出的非线性系统

令观测误差向量e～ = e − eˆ ．

若 f (X)和 g (X)可知，则系统最优控制律为

若 f (X)和 g (X)未知，分别用其估计值 fˆ(Xˆ)和gˆ(Xˆ )代替，则系统最优控制律为

式中：uD为鲁棒控制项；uS(X ˆ ) 为监督控制项；uC( X ˆ /β)为变论域模糊控制项；β为变论域模糊控制器伸缩因子．

由式(1)～式(5)可得

式中 Δ g ( X,Xˆ ) = gˆ ( X ˆ ) − g(X)．

若观测器亦选如下形式

则可得改进观测误差方程为

式中，观测增益向量 kT=[kn kn −1 … k 2 k1]．

若通过选择向量k和 kc，使系数阵 ( A − k CT−B)的特征多项式严格 Hurwitz稳定，则存在对称矩阵P，使得

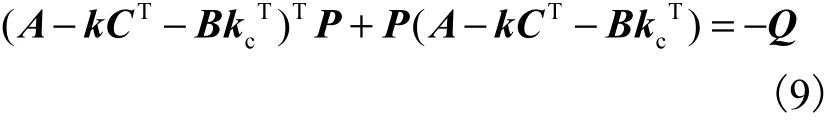
式中Q为任意的正定矩阵．

有关李亚普诺夫函数的选取，以及监督控制律uS( Xˆ ) 、变论域模糊控制律 uC(X ˆ /β)、伸缩因子α和β的自适应律与文献[4]中结论相同．

鲁棒控制项 uD表达式的推导过程与文献[4]中相同，结论形式也类似．但由于观测误差方程表达式的变化，不确定项θ表达式需要修正．新的鲁棒控制项uD的表达式为

式中：sgn(x) 为符号函数；β*和α*分别为β和α的最优参数．

由于仅输出y和参考信号向量yr已知，观测误差向量e～是不可获得的.但如果调整控制器参数，使得满足如下假设，则式(8)和式(10)可实现．

假设：伸缩因子β 经过足够小的变化调整，就能逼近到β*．通过鲁棒补偿控制律 uD补偿后，不确定项θ对稳定设计的影响足够小.

式(9)中观测误差方程的系数阵为 ( A −kCTB kcT).而文献[4]中的观测误差方程的系数阵为 ( A−kCT)．并且，要求选取反馈增益向量k，使得 ( A−kCT)的特征多项式严格 Hurwitz稳定．则存在对称矩阵 P0，使得

式中0Q为任意的正定矩阵．

改进后的式(9)，说明不仅要考虑选择观测增益向量k，反馈增益向量 kc也和观测误差向量收敛的速度大小有直接关系．一般在左半s平面上，观测器(A−kCT)的Hurwitz稳定的根位置，要远离控制器(A−B)的Hurwitz稳定的根位置[9]．对于式(8)中观测误差方程的特征系数矩阵而言，当选择观测增益向量k的增益越高，则反馈增益向量 kc对观测误差向量收敛的速度的影响就越小．而高增益观测增益向量k使得闭环极点右移，稳定性变差，对闭环系统控制是不利的．所以，在变论域模糊控制稳定设计中，根据改进后的式(9)，综合考虑选择观测增益向量k与反馈增益向量ck更合理些．

1.2 自组织结构算法

文献[8]和文献[10]中，分别针对模糊系统和神经网络系统，给出了相应的自组织结构算法．而文献[8]和[10]中基于“当前”的控制情况，对整个模糊系统结构缺乏考虑．结合变论域模糊控制器特点，这里给出新的自组织结构算法的实现步骤．

对于一个模糊系统，设 Xi=[− Ei, Ei](i = 1 ,2,… ,n)是输入变量 xi(i = 1 ,2,… ,n )的论域，Y = [− U ,U]是输出变量y的论域． Ai= { Aij}(1≤j≤m)是论域 Xi上的一个模糊划分．B = { Bj}(1≤j≤m)是Y的模糊划分，yj是 Bj的峰点．从模糊规则结构上看，Ai和B分别是前件和后件的模糊划分．

（1）||eˆ||反映当前模糊控制器是否适当.定义W(t)和 G(t)，分别为上下界时变函数.e0＞ 0 为设计参数.当||eˆ||∈[G(t),W(t) + e0]时，当前模糊系统的结构是适当的;当||eˆ ||∈ [W (t) + e0,+ ∞]时，需增加模糊系统的规则；当||eˆ||∈[0,G(t ))时,则需减少模糊系统的规则.

通常取

式中λ为正定常衰减率．根据要求的精度来设定0e．

(2)定义jz是前件隶属度函数中心．当同时满足以下2个条件时，需要增规则

式中：μ为正的阈值；z+是离当前模糊系统输入()xt最近的隶属度函数中心，即

新加的模糊子集初值设定为：取当前输入 ()xt作为新模糊前件隶属度函数的中心，当前模糊系统的输出作为新模糊后件的jy．

(3)减规则判断条件为

式中1T为设计参数，1T0＞.

式中：jr为模糊基函数；0Δ＞为匹配度设计参数.

文献[8]中，仅要求式(15)符合||eˆ||＜G(t)．若整个控制系统的跟踪误差处于振荡发散时，仅根据某时刻||eˆ||＜G(t),就判断系统已经稳定在一定跟踪精度范围，显然是不正确的.

(4)规则替换

文献[8]中提出，当到达规则数量上限时，与当前模糊输入距离最远的模糊子集被替换掉．

从整个控制过程来看，文献[8]的替换操作中认为，距离当前最远的模糊子集的信息对当前控制影响最小．但文献[8]的替换操作，不能保证被替换模糊子集的信息对整个控制过程影响最小．如果把相邻模糊子集的间距以相邻模糊子集的峰点间距为定义，则从整个论域上看，峰点间距越密，该划分信息的冗余就越大[11-12]．所以，文献[8]中的规则替换，不仅要考虑距离当前模糊输入的远近，还应该考虑模糊子集合包含冗余信息的多少．进而改进为被替换模糊子集满足，距离当前输入超过一定距离 λ1，并且被替换模糊子集相邻间距小于λ2．在所有满足替换条件的模糊子集中，距离当前输入最远的模糊子集将被替换掉．其中的减规则参数 T1，以及替换规则参数λ1和λ2，可通过具体系统仿真效果反复调试确定．值得注意的是，增规则中的μ和替换规则中 λ2是不同的．增规则中，虽然阈值μ保证相邻模糊子集的间距必须超过一定限度，即考虑当前所增加模糊子集的冗余信息要小．这里的λ2保证在满足与当前模糊输入一定距离的基础上，要选择冗余信息比较大的做为被替换模糊子集．

新替换模糊子集初值设定如下：取当前输入 ()xt作为新模糊前件隶属度函数的中心，当前模糊系统的输出作为新模糊后件的jy．

通过自组织结构算法，保证变论域模糊控制器的模糊结构具有“合适规模”．进而动态减小式(10)中不确定项中的模糊逼近误差．从而，鲁棒控制项的幅值选取不必很大．甚至当模糊逼近误差很小时，可以不设计鲁棒控制项Du．

1.3 带自组织结构算法变论域模糊控制器稳定性

文献[8]证明了所提出的自组织结构算法并不影响其控制系统的稳定性．这里亦可规定，在t时刻自组织结构算法起作用．由第 1.2节可知，自组织结构算法保证了控制输入的连续性，即 u(t−) = u (t+)．进而由式(1)可得 X ( t−) = X ( t+)．所以有e～ ( t−) = e～ ( t+)．而自适应律[4]1018为

式 中 ： β～ = β*− β ,α～ = α*− α ，可 得 β (t−) = β (t+)和α(t−) = α (t+)．

最后，由李亚普诺夫函数[4]1018

可得 V (t−) = V (t+)．因此，变论域模糊控制器由李亚普诺夫方法所保证的稳定性，并不受所加入的自组织结构算法影响．

2 Chua′s混沌系统的仿真

Chua′s混沌电路动态方程经过线性变换后的状态方程和输出方程为

控制的目的是使得状态变量x1，跟踪给定的参考信号 yr(t) = 9 sint．设定约束[4]1021为

式中：f0和 g0分别是函数f和g的上界函数和下界函数；gL是函数g的下界函数．

为了验证改进变论域控制器的有效性，先用文献[4]中控制 器 ，实现有 关 控制目标 ．uC(X ˆ /β)和gˆ(X ˆ /α)分别逼近u*和g(X)，其中α和β为用自适应律调节的伸缩因子．然后，在原来的控制器基础上，加入有关改进算法．

取观测器增益向量 kT=[52373]．取反馈增益向量为=[123]．自适应律调节的自适应系数γ= 0 .0009．由式(10)，鲁棒控制项设计为

式(11)中的

取误差e和误差变化率e˙的模糊论域分别为E和EC.由式(2),e和 e˙亦可记为1e和2e.若定义,分别是模糊论域E和EC上的模糊划分, B = { Bj}(1≤j≤m)是Y的模糊划分．A1j与 A2j分别称为 A1与 A2的模糊子集．E和EC上的隶属度函数,分别如图1(a)和图2(a)所示.

模糊规则可以选取为：若E是 A1j，并且EC是A2j，则Y是 Bj( j = 1,2,… ,m ).

图1 e的隶属函数Fig.1 Membership function of e

图2 e˙的隶属函数Fig.2 Membership function of e˙

改进控制器在式(9)中的

若记μe和μe˙分别为自组织结构算法对模糊论域E和EC进行增规则操作时的阈值μ，并记λ1e为改进后自组织结构算法对模糊论域E进行替换规则操作时的依据λ1，同理，λ2e、λ1e˙和λ2e˙有类似定义．自组织结构算法部分参数为λ=20,G ( 0)=0.1,W ( 0) = 0 .5,e0= 0 .1,μe=0.062,μe˙=0.4,Δ=0.25,T1=0.02s,λ1e=1.7,λ2e=0.3,λ1e˙=6,λ2e˙=0.5.

在改进后控制器作用下，经过30 s调节后，E和EC上的隶属度函数分别如图1(b)和图2(b)所示．这时隶属度函数为

图3 e的响应Fig.3 Response of e

图 4 e˙的响应Fig.4 Response of e˙

图 3和图 4分别给出了e和e˙的动态响应曲线．由图3和图4可以看出，改进后的控制器对跟踪误差的响应有明显改善．

3 结 语

针对一类变论域模糊控制器中未考虑反馈增益向量对观测器估计误差影响的问题，给出修正的稳定设计．针对一类在线自组织结构算法中，基于“当前”的控制情况，而对整个模糊系统结构缺乏考虑的问题，给出一种新的自组织结构算法．为了减小不确定项的界函数对鲁棒控制项设计的影响以及提高原变论域模糊控制器的适应性，将新的在线自组织结构算法运用到改进变论域自适应模糊控制中．尤其注意的是，这种自组织结构算法并不影响由李亚普诺夫方法所保证的变论域模糊控制器的稳定性．所提出的有关改进，对系统跟踪误差的收敛、闭环稳定性和模糊系统逼近都有贡献．仿真研究表明所提出的改进是有效的．

［1］ 李洪兴. 四级倒立摆的变论域自适应模糊控制[J]. 中国科学 E 辑，2002，32(1)：65-75.

Li Hongxing. Variable universe adaptive fuzzy control on the quadruple inverted pendulum[J]. Science in China Seri E，2002，32(1)：65-75(in Chinese).

［2］ Shan Weiwei，Ma Yuan，Ncwcomb R W，et al. Analog circuit implementation of a variable universe adaptive fuzzy logic controller[J]. IEEE Trans on Circuits and Systems，2008，55(10)：976-980.

［3］ Wang Jiang，Zhang Zhen，Li Huiyan. Synchronization of Fitz-Hugh-Nagumo systems in EES via H∞variable universe control[J]. Chaos，Solitons and Fractals，2008，36(5)：1332-1339.

［4］ Wang Jiang，Qiao Guodong，Deng Bin. Oberver-based robust adaptive variable universe fuzzy control for chaotic system[J]. Chaos，Solitons and Fractals，2005，23(3)：1013-1032.

［5］ Wang L X. Stable adaptive fuzzy control of nonlinear systems[J]. IEEE Trans on Fuzzy Syst，1993，1(2)：146-155.

［6］ 胡跃明. 变结构控制理论与应用[M]. 北京：科学出版社，2003.

Hu Yueming. Variable Structure Theory and Its Applications [M]. Beijing：Science Press，2003(in Chinese) .

［7］ Chen Chaio-shiung. Adaptive fuzzy control systems with dynamic structure [J]. International Journal of Systems Science，2008，39(2)：163-172.

［8］ Phan P A，Gale T J. Direct adaptive fuzzy control with a self-structuring algorithm [J]. Fuzzy Sets and Systems，2008，159(8)：871-899.

［9］ 张 莲，胡晓倩，王士彬，等. 现代控制理论[M]. 北京：清华大学出版社，2008.

Zhang Lian，Hu Xiaoqian，Wang Shibin，et al. Moden Control Theory [M] . Beijing：Tsinghua University Press，2008(in Chinese) .

［10］ Chen Chaio-Shiung. Dynamic structure neural-fuzzy networks for robust adaptive control of robot manipulators [J]. IEEE Trans on Industrial Electronics，2008，55(9)：3402-3414.

［11］ Jin Yaochu. Fuzzy modeling of high-dimensional systems：Complexity reduction and interpretability improvement[J]. IEEE Trans on Fuzzy Systems，2000，8(2)：212-221.

［12］ 李盼盼，朱伟兴. 基于改进遗传算法的 TS模糊模型的优化设计[J]. 传感器与微系统，2008，27(8)：100-102.

Li Panpan，Zhu Weixing. Optimized design of TS fuzzy model based on improved genetic algorithm [J]. Transducer and Microsystem Technologies，2008，27(8)：100-102(in Chinese) .