两边连接钢板剪力墙试验与理论分析
马欣伯,张素梅,郭兰慧
(1. 哈尔滨工业大学土木工程学院,哈尔滨 150090;2. 住房和城乡建设部科技发展促进中心,北京 100835)
钢板剪力墙是建筑结构中的一种新型抗侧力构件,与最为常用的钢筋混凝土剪力墙相比,其刚度适中,在地震荷载作用下承受适度的水平地震力,通常表现为延性破坏,避免了钢筋混凝土剪力墙因刚度较大而在地震中承受较大的水平力,裂缝出现较早且呈现脆性破坏的缺点,具有较强的耗能能力.同时,因其厚度较小而节约了使用空间,减轻了结构自重,节约了基础造价,地震破坏后容易修复[1].
目前国内外针对与周边框架梁、柱均连接(四边连接)钢板剪力墙的研究和应用较多.由于薄钢板在抵抗剪力初期即发生屈曲,我国规范[2]建议采用厚钢板或设置纵向和横向加劲肋的钢板剪力墙,但在使用过程中并不经济.加拿大和美国学者注意到受剪薄钢板的屈曲后性能,于20世纪70年代开始对四边连接且未设置加劲肋的薄钢板剪力墙进行了较为系统的试验研究与理论分析,获得了其抗震性能方面的诸多研究成果,并先后被加拿大及美国规范采用 .研究表明:尽管其具有较高的承载力和耗能能力,但框架梁、柱作为嵌固边界对四边连接钢板剪力墙的性能影响显著,薄钢板剪力墙中沿对角线方向形成的拉力带使框架柱中产生较大的弯矩,厚钢板剪力墙因面内均匀受剪使框架柱中产生较大的轴力,上述因素往往造成框架柱过早破坏,严重影响钢板剪力墙抗震性能的充分发挥[5].此外,钢板沿整跨布置不利于开设过道和门窗,难于满足建筑使用功能的要求.
两边连接钢板剪力墙由钢板和周边框架组成,钢板通过高强螺栓或焊缝仅与框架梁连接.该种剪力墙消除了对柱子的依赖,避免了框架柱过早破坏;小跨高比的两边连接钢板剪力墙布置灵活,可以在一跨中分段布置,便于门窗、过道的布置,且通过调整钢板尺寸或墙板数量,使剪力墙的刚度和承载力发生改变,方便工程师进行不同部分结构刚度匹配地调整.在实际工程应用时,待框架结构施工完毕后再安装钢板剪力墙,进而使剪力墙在受力过程中仅承受水平剪力,而不承担竖向荷载.
美国的Xue和Lu[6-7]两位学者于1994年率先提出该种剪力墙,并对其进行了数值分析,研究表明该种剪力墙及其组成的结构体系具备良好的承载力和耗能能力;2004年清华大学的缪友武[8]采用有限元方法对其进行了研究.截至目前,国内外鲜见关于两边连接钢板剪力墙试验研究的报道,理论研究也不够深入,还需对其进行系统的试验研究与理论分析,进而探讨其抗震性能与工作机理.
1 试验方案
1.1 试件设计与材料属性
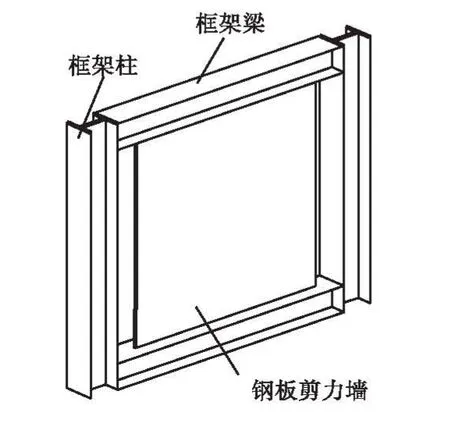
图1 两边连接钢板剪力墙Fig.1 Steel shear wall with two-side connections
试验设计了缩尺比为1∶3的两边连接钢板剪力墙试件(如图 1所示),试件尺寸如图 2所示.螺栓中心线间钢板的跨高比 L/H为 1.0,加工过程中对螺栓孔附近区域的钢板表面进行喷砂处理以提高接触面的摩擦系数.钢材厚度 2.75 mm,相应钢板高厚比 λ为400,通过标准试件的拉伸试验获得的钢材应力-应变关系曲线具有明显的屈服平台,其屈服强度 fy为294.65 N/mm2,抗拉强度fu为429.90 N/mm2,弹性模量 Es为 2.151×105N/mm2,泊松比ν 为 0.306,延伸率35.46%.

图2 钢板剪力墙试件Fig.2 Specimen of shear wall
1.2 试验装置
采用拟静力试验分析两边连接钢板剪力墙在低周往复荷载作用下的抗震性能,试验在日本建研式水平加载装置上进行(如图3所示),电液伺服作动器一端固定在反力墙上,另一端与加载装置的“L”形梁固定,侧边设置 4个侧向支撑并通过光滑滚轴与“L”形梁接触,以防止其发生面外位移或晃动.为使剪力墙承担作动器施加的全部水平荷载而不承担竖向荷载,在水平加载装置内安装一铰接框架,通过压梁与水平加载装置相连.剪力墙试件采用摩擦型高强螺栓通过角钢与铰接框架进行连接(如图 4所示),为防止钢板发生滑移,保守地按每个螺栓承受的剪力大于所分担钢板区域达到极限抗拉强度的原则进行设计,同时考虑钢板鼓曲引起的翘力影响,通过计算[9]确定钢板与角钢的连接螺栓采用 10.9级 M20高强螺栓,角钢与钢梁的连接螺栓采用8.8级M20高强螺栓,其间距均为 70,mm,螺栓孔直径均为22,mm.
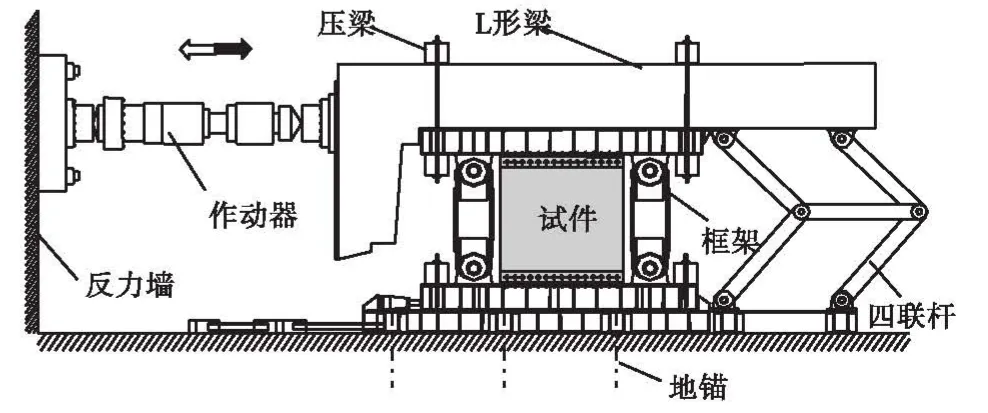
图3 试验装置示意Fig.3 Testing setup
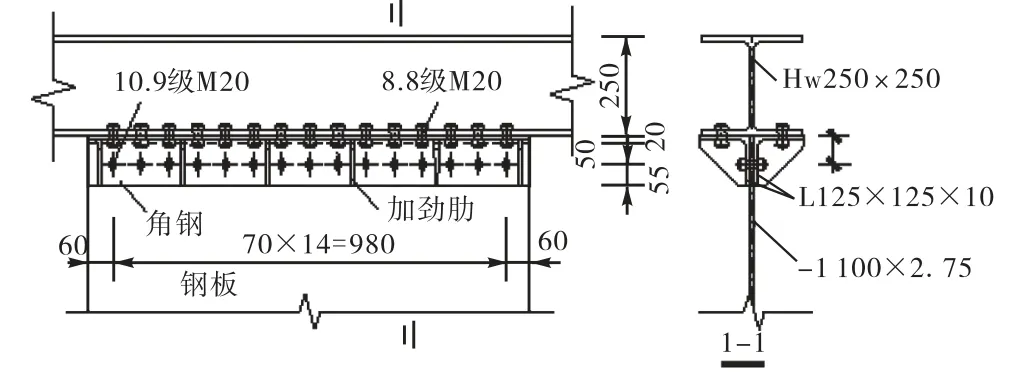
图4 连接方式Fig.4 Details of connection
1.3 加载方式
根据《建筑抗震试验方法规程》(JGJ 101-96)[10]的规定,在正式试验前先进行预加载以检查试验量测设备是否正常.正式加载时由正向开始加载,采用荷载-位移双控制的方法,即试件屈服前,根据预先预测的屈服荷载,采用荷载控制分级加载,直至试件屈服,该阶段对应于每级荷载循环 1次;试件屈服后,采用位移控制加载,以试验测得的屈服位移的倍数分级施加,该阶段对应每级荷载循环2次.
1.4 数据采集
试验中所施加的水平力由作动器上的荷载传感器直接测得,位移则通过高精度位移计测量.测量水平位移的位移计在顶梁两侧对称布置,将两者测得的数据取平均值以消除框架面外扭转的影响,并根据实际情况在钢板背面布置位移计测量试件的面外变形,荷载值和位移实时采集,以便于监控试验进程,确定屈服荷载和屈服位移.此外,为监测钢板的内力分布情况,在钢板中部和角部对称布置三向应变花,其数值由静态应变测量系统采集,每级荷载幅值和荷载卸载至零时刻时各采集 1次.由于着重从宏观上展示该类钢板剪力墙在往复荷载作用下的耗能性能,进而揭示该类剪力墙的抗震性能,因此对钢板在抗剪过程中局部的应变与应力情况暂不做详细介绍.
2 试验现象
在弹性加载阶段,起初的几个荷载循环并无明显现象,当荷载加至±80,kN时,试件负向位移为3.3,mm(层间侧移角1/300左右),此时钢板角部在局压作用下出现鼓曲,板心的最大面外位移为16.5,mm;继续加载至±160,kN 时,试件负向位移达到8.5,mm(层间侧移角1/130左右),钢板除在角部出现的鼓曲外,沿钢板对角线方向的鼓曲逐渐形成(即拉力带形成,如图 5(a)所示),在该阶段的反向加载过程中,钢板沿对角线方向的鼓曲由一个方向向另一个方向转换,角部的鼓曲位置随之发生变化,波形转换过程伴有巨大响声,但转换前后钢板鼓曲方向没有变化,板心的最大面外位移为26.7,mm.
进入弹塑性阶段后,当位移加载至±12,mm(层间侧移角 1/100左右)时,钢板的变形特征保持不变,板心的最大面外位移达到 31.7,mm,波形转换过程中产生“跃越失稳”现象并伴随清脆响声;当位移加载至±16,mm(层间侧移角1/70左右)时,钢板鼓曲已相当明显,沿对角线方向开始形成 2条半波拉力带,此时板心的最大面外位移达到36,mm,为防止损坏将面外位移计拆下;此后随位移继续增加,钢板沿对角线方向形成的 2条拉力带愈加明显(如图 5(b)所示),尽管试件在往复荷载作用下仍存在“跃越失稳”现象,但波形转换过程中的响声逐渐减弱,钢板面外变形逐渐增大的过程中板心处的鼓曲方向始终保持不变.当加载至±40,mm(层间侧移角 1/28左右)时,尽管试件仍未出现明显破坏现象,但由于水平位移计已经达到量程,结束试验.试验结束卸载后发现,钢板仍存在较大的残余变形(如图5(c)所示).

图5 试验现象Fig.5 Experimental phenomenon
3 试验结果分析
3.1 滞回曲线与骨架曲线
图 6为试件的荷载-位移(V-Δ)滞回曲线.由图6中可见:在弹性加载阶段,试件的承载力随水平位移地增加近似呈线性增大,滞回环包围的面积较小,基本不具备耗能能力.进入弹塑性阶段后,承载力提高幅度逐渐减慢,波形转换过程中产生的“跃越失稳”使滞回曲线出现波动,且由于试件在反向加载时需首先恢复已经形成的鼓曲,滞回曲线出现“捏缩”现象并随位移增加逐渐加重;当正向位移加载至 19.6 mm(层间侧移角 1/55左右)时,试件达到正向极限承载力 206.94,kN;当负向位移达到-18.6,mm 时,试件达到负向极限承载力 202.36,kN.图 7绘出了试件的骨架曲线,其主要指标见表 1,表中 Δy为屈服位移,Vy为屈服承载力,Δu为极限位移,Vu为极限承载力,Δmax为试验结束时的最大位移,Vmax为最大位移时的承载力.可以看出:该试件的骨架曲线具有较好的对称性,且包括弹性、弹塑性和塑性3个阶段,塑性阶段的承载力随位移增加下降缓慢,直至试验结束时承载力仍未下降到极限承载力的 85%,说明该试件具有良好的延性,正向荷载作用下的延性系数大于 5.32,负向荷载作用下的延性系数大于3.95.

图6 试件的滞回曲线Fig.6 Hysteretic curves of specimen
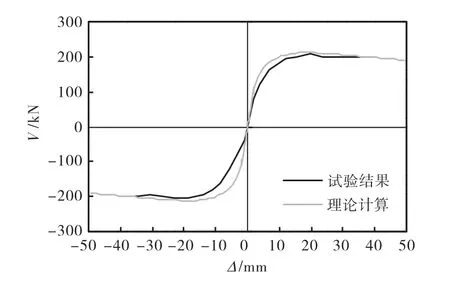
图7 试件的骨架曲线及与有限元结果对比Fig.7 Skeleton curve of specimen and comparison with Fig.7 FEM results

表1 试件骨架曲线主要指标及与有限元结果对比Tab.1 Values on the skeleton curve of specimen and compared with FEM results
3.2 耗能面积与能量耗散系数
图8和图9分别为滞回环面积Ad及能量耗散系数E随位移Δ的变化曲线.由图中可见:在弹性加载阶段,滞回环包围的面积较小,能量耗散系数在 0.4左右,基本不具备耗能能力;进入弹塑性后,试件的滞回环面积随位移呈线性增加,当位移加载至±12 mm(层间侧移角 1/100左右)时,能量耗散系数迅速提高至 0.8左右并保持不变,钢板已经开始通过塑性变形耗能;当位移达到±24,mm(层间侧移角 1/45左右)时,能量耗散系数继续小幅度提高,此后保持在0.9左右,直至试验结束.整个试验过程中,尽管滞回曲线出现“捏缩”现象并逐渐加重,但滞回环面积始终线性增大,能量耗散系数相对稳定,说明其具备良好的耗能能力.

图8 试件的Ad-Δ曲线Fig.8 Ad-Δ curve of specimen
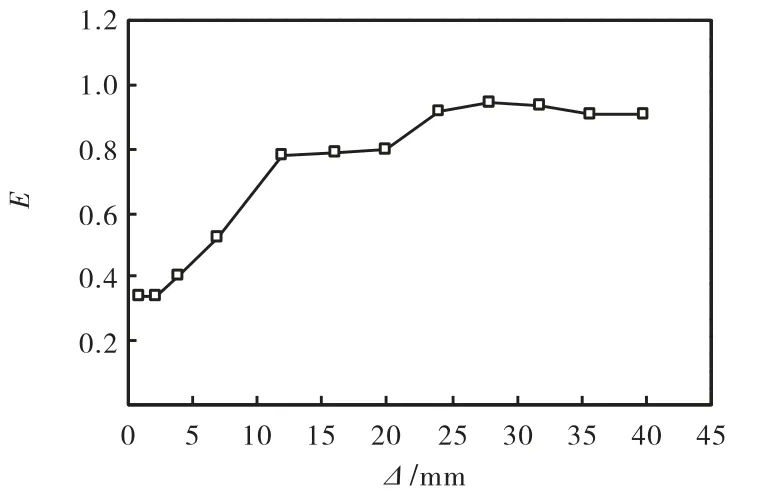
图9 试件的E-Δ曲线Fig.9 E-Δ curve of specimen
3.3 割线刚度
图10 为试件的割线刚度K随位移 Δ的变化曲线,由图 10可见,试件的割线刚度随水平位移的增大而降低,但降低的幅度逐渐减小.
3.4 试验总结
综上所述,两边连接钢板剪力墙试件在抗震规范[11]规定的多遇地震作用下的层间侧移角 1/300内均处于弹性阶段,具备较高的刚度和承载力;超过规范规定的罕遇地震作用下的层间侧移角 1/50时,试件以沿对角线形成的拉力带发展塑性耗能,屈曲后强度得以充分发展,尽管滞回曲线出现“捏缩”现象,但剪力墙仍具备稳定的承载能力和耗能能力,且具备良好的延性.采用该剪力墙的结构符合“小震不坏、中震可修、大震不倒”的抗震设计原则和“三个水准”的抗震设防要求.但该类剪力墙的缺点在于其在往复荷载作用下将产生较大的面外变形且难于修复,波形转换过程中发出的清脆响声使人产生恐惧感.
与钢筋混凝土剪力墙相比,近年来尽管有许多学者对钢筋混凝土剪力墙的抗剪性能进行了改进,使其延性得到改善,但从试验结果看,当层间侧移角超过1/30后,钢板剪力墙试件尚未发生破坏,若继续加载仍能保持稳定的承载力和延性;而对于钢筋混凝土剪力墙,达到如此大的层间侧移角,由于混凝土开裂将难以保证其仍具备稳定的耗能能力和延性.
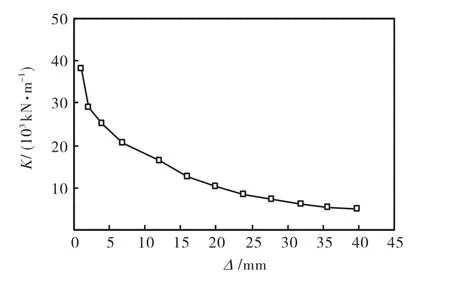
图10 试件的K-Δ曲线Fig.10 K-Δ curve of specimen
4 有限元分析
4.1 有限元模型建立
为检验有限元分析方法的可行性,本文采用Ansys有限元软件建立了如图11(a)所示的简化力学模型.其中梁、柱采用 BEAM189单元模拟,钢板采用 SHELL181单元模拟.模型中框架梁、柱均按试验中的实际尺寸建立,且节点为铰接,支座位于低梁两端并采用铰支形式,水平荷载以集中力的形式作用于顶梁端部,有限元模型如图 11(b)所示.在进行有限元分析前,考虑到钢板剪力墙在形成拉力带后进入大变形状态,曾采用了与实际钢材本构关系更为相近且考虑了强化阶段的“三折线”本构关系模型进行了计算,结果表明,采用“理想双线性本构关系模型”的计算结果与试验结果更为接近,因此在分析过程中,对钢材的本构关系采用理想双线性模型,对施加的初始缺陷采用一阶弹性屈曲模态,其幅值根据实测情况取为钢板跨度的1/100.

图11 试件的简化力学模型和有限元模型Fig.11 Simplified mechanical model and FEM model of specimen
4.2 试验结果与有限元结果对比
图 7为采用有限元得到的荷载-位移曲线与试验骨架曲线对比.可以看出:单向加载时有限元方法获得的荷载-位移曲线与试验得到的骨架曲线趋势相同,且与正向加载时骨架曲线的吻合程度优于负向加载时的骨架曲线,计算曲线与试验曲线在弹性阶段吻合较好,而进入弹塑性阶段两者间的差距较大,这是因为在试验过程中螺栓连接处的钢板难以避免地发生一定滑移,并且有限元结果并非采用试验中的循环加载获得,忽略了循环荷载作用下累积损伤等因素的影响.表 1中列出了两者初始刚度、屈服荷载和极限荷载的对比结果,可见理论计算结果均比试验结果高,除初始刚度的计算结果比试验结果高 50.7%差距较大外,屈服荷载和极限荷载的计算结果与试验结果的差距均较小,分别仅为2.0%和2.2%,进而说明采用有限元方法对两边连接钢板剪力墙进行理论分析是可行的.
4.3 理论分析
采用有限元方法对两边连接钢板剪力墙的进行理论分析时,为使框架梁、柱在受力过程中不先于墙板发生破坏,以便重点分析剪力墙的受力机理,在如图 11(a)所示的简化模型中,框架梁、柱的抗弯刚度和抗压刚度均取无穷大.采用有限元方法分析了跨高比L/H和高厚比λ对其抗剪性能的影响,其中钢板高度H为3,000,mm保持不变,跨高比的变化范围为0.5~2.0,高厚比的变化范围为 100~500,钢材屈服强度 fy为 235,N/mm2,弹性模量 Es为 2.06×105N/mm ,剪切模量Gs为7.9×10,N/mm .
图12分别为不同λ和L/H下的平均剪应力τ(剪力与钢板截面面积的比值)随层间侧移角θ的变化曲线(τ-θ 曲线).由图中可见:不同λ和 L/H 下的 τ-θ 曲线均存在弹性、弹塑性及下降段 3个阶段,且都存在峰值点,但弹塑性阶段随λ较减小而不明显;当L/H一定时,τ-θ曲线的峰值点随λ的降低而逐渐增高,但下降段的斜率随之增大,构件的延性逐渐降低;当λ一定时,τ-θ曲线的峰值点随L/H的增大而逐渐增高,但下降段的斜率变化不大.此外,不同λ下的 τ-θ曲线随λ的增大而逐渐接近.
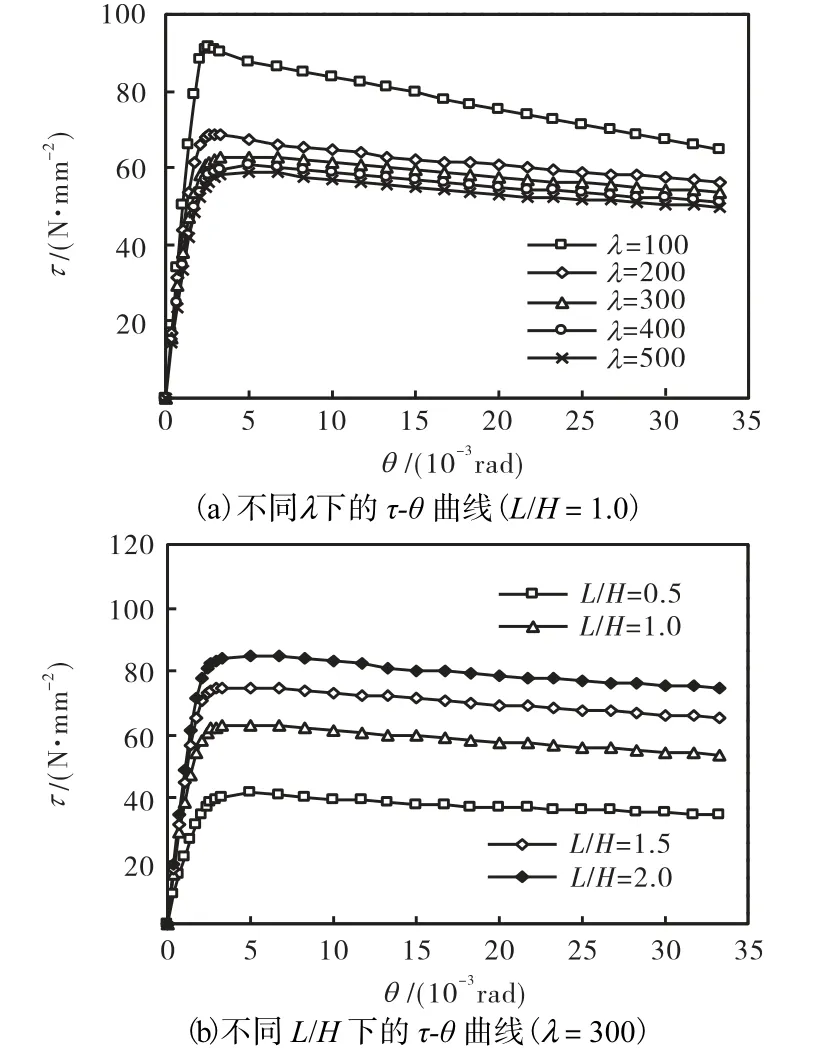
图12 不同λ和L/H下的τ-θ曲线Fig.12 τ-θ curves under different λ and L/H
图13 为极限平均剪应力τu与钢材屈服剪应力fv的比值随λ和 L/H 的变化曲线.由图中可见:当 L/H一定时,τu随λ的增大而减小,但减小的幅度逐渐降低;当λ一定时,τu随 L/H 的增大而增大,但增大的幅度逐渐降低;由此说明采用厚板或大跨高比板将获得较高的平均应力水平,更充分地利用材料强度,但不够经济.
将 τ-θ曲线在原点处的斜率定义为“初始等效剪切模量”,用“Geq0”表示,其单位为 N/mm2.Geq0与初始刚度K0存在换算关系Geq0=K0H/A,其中A为受剪面面积.图 14为不同λ下初始等效剪切模量与钢材剪切模量比值 Geq0/Gs随 L/H的变化曲线,由图中可见:不同λ下的 Geq0/Gs-L/H曲线几乎重合, Geq0随 L/H的增大而增大,但增大的幅度逐渐减小,由此说明Geq0与λ的大小无关,仅受L/H的影响.

图13 τu /fv 随λ和L/H变化的关系曲线Fig.13 τu /fv-λ and τu/fv- L/H relative curves under different L/H and λ
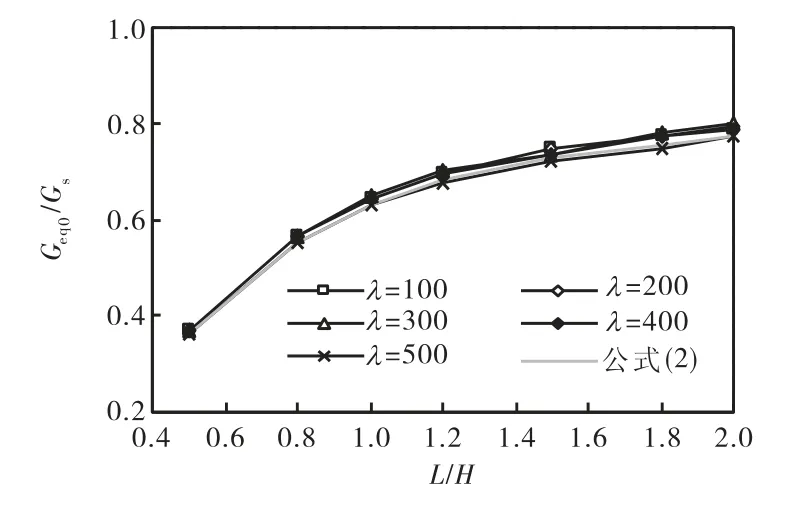
图14 不同λ下Geq0/Gs随L/H的变化曲线Fig.14 Geq0/Gs-L/H curves under different λ
5 骨架曲线的简化计算模型
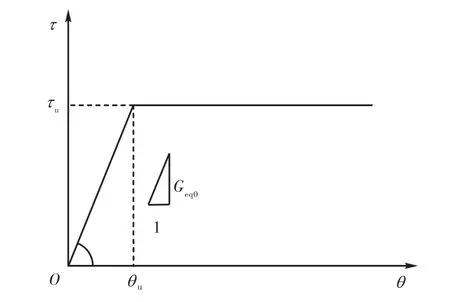
图15 τ-θ骨架曲线的简化计算模型Fig.15 Simplified model of τ-θ skeleton curve
综合考虑各参数下 τ-θ曲线的形状,为便于实际应用,本文将其简化为如图 15所示的理想双折线模型,该曲线分弹性段和塑性段,弹性段的斜率为初始等效剪切模量 Geq0,超过极限平均剪应力 τu后,τ保持不变.
5.1 初始刚度和等效剪切模量的确定
由试验和理论分析可知,两边连接钢板剪力墙在初始阶段以面内受力为主,根据结构力学中位移计算的一般公式[12],两端固定构件在水平荷载作用下的总水平位移由弯矩引起的水平位移和剪力引起的水平位移2部分组成,由此可推导出计算初始刚度的公式为
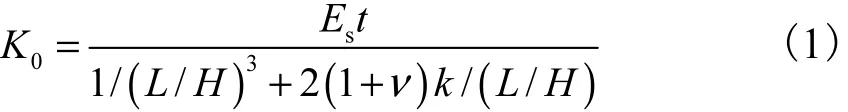
则初始等效剪切模量的计算公式为
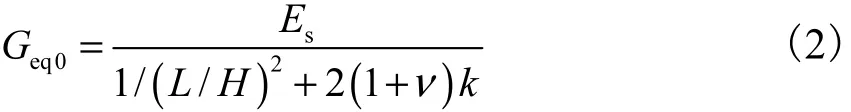
式中:v为钢材泊松比;k为截面修正系数(对于矩形截面取1.2).由式(2)可见,当材料属性一定时,初始刚度除与钢板跨高比有关外,还与钢板厚度有关,而初始等效剪切模量只与钢板跨高比有关,这与图 14揭示的理论分析结论相同.将采用式(2)得到的理论结果与相应有限元结果进行对比(如图 14所示),两者吻合较好,最大仅相差2.2%.
5.2 极限承载力的确定
对不同参数下的极限承载力有限元分析结果进行拟合,得计算极限平均剪应力的公式为
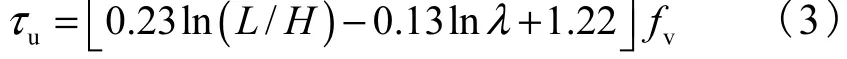
将采用式(3)得到的计算结果与相应有限元结果进行对比,两者比值的均值为1.002,方差为0.045,两者吻合较好.
5.3 简化模型与有限元结果对比
图16为骨架曲线简化模型结果与相应有限元结果对比,由图中可见,所提出的简化模型能够较好地反映两边连接钢板剪力墙的骨架曲线,但相对高估了试件后期的承载力和延性.
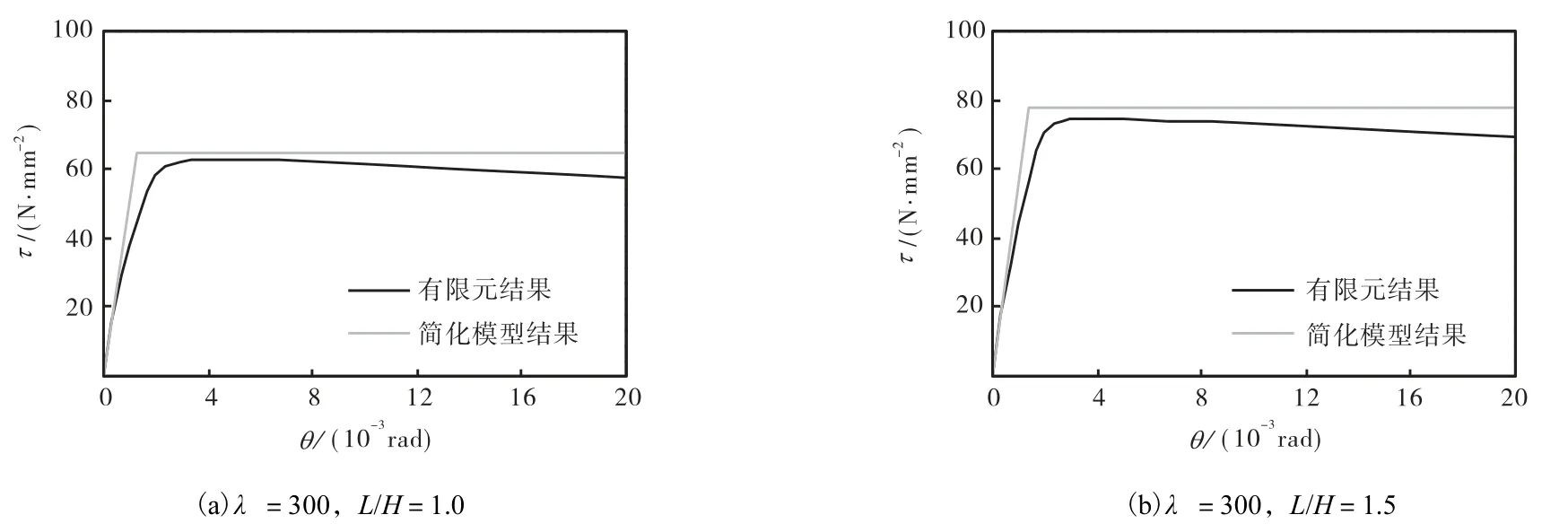
图16 简化模型与有限元骨架曲线对比Fig.16 Comparison between skeleton curve of simplified model and that of FEM results
6 结 语
两边连接钢板剪力墙具有较高的初始刚度和承载力,在受荷后期通过沿对角线形成的拉力带发展塑性承担荷载并耗能,尽管滞回曲线出现“捏缩”,但其仍具有稳定的耗能能力和良好的延性,符合现行国家规范的设计要求,其极限承载力随钢板高厚比和跨高比的增大而增大,该类剪力墙的骨架曲线可采用本文提出的理想双线性简化模型计算得到.
[1] Astaneh-Asl A. Seismic behavior and design of steel shear wall. Steel Tips Report [R]. American Structural Steel Educational Council,2001.
[2] 中华人民共和国行业标准. JGJ 99-98 高层民用建筑钢结构技术规程[S]. 北京:中国建筑工业出版社,1998.
Trade Standard of PRC. JGJ 99-98 Technical Specification for Steel Structures of Tall Buildings [S]. Beijing:China Architectural Industry Press,1998(in Chinese).
[3] Canadian Standard Association. CAN/CSA-S16.1-94 Limit State Design of Steel Structures [S]. Toronto,Ontario,1994.
[4] American Institute of Steel Construction. ANSI/AISC 341-05 Seismic provisions for Structural Steel Buildings [S]. 2005.
[5] Lubell A S,Prion H G L. Unstiffened steel plate shear wall performance under cyclic loading [J]. Journal of Structural Engineering,2000,126(4):373-385.
[6] Xue M,Lu L W. Interaction of infilled steel shear wall panels with surrounding frame members [C] // Proceedings of Structural Stability Research Council Annual Technical Session. Bethlehem,PA,1994:339-354.
[7] Xue M,Lu L W. Monotonic and cyclic behavior of infilled steel shear panels [C] // Proceedings of 17th Czech and Slovak International Conference on Steel Structures and Bridges. Bratislava,Slovakia,1994:152-160
[8] 缪友武. 两侧开缝钢板剪力墙性能研究[D]. 北京:清华大学土木水利学院,2004.
Miao Youwu. The Investigation to Structural Behavior of Steel Plate Shear Wall slotted at Two Edges [D]. Beijing:School of Civil Engineering,Tingshua Universigy,2004(in Chinese).
[9] 中国人民共和国国家标准. GB 50017—2003 钢结构设计规范[S]. 北京:中国计划出版社,2003.
National Standard of PRC. GB 50017—2003 Code for Design of Steel Structures [S]. Beijing:China Planning Press,2003(in Chinese).
[10] 中华人民共和国行业标准. JGJ 101-96 建筑抗震试验方法规程[S]. 北京:中国建筑工业出版社,1997.
Trade Standard of PRC. JGJ 101-96 Specification of Testing Methods for Earthquake Resistant [S]. Beijing:China Architectural Industry Press,1997(in Chinese)
[11] 中华人民共和国国家标准. GB 500011—2001 建筑抗震设计规范[S]. 北京:中国建筑工业出版社,2001.
National Standard of PRC. GB 50011—2001 Code for Seismic Design of Buildings [S]. Beijing:China Architectural Industry Press,2001(in Chinese).
[12] 龙驭球,包世华. 结构力学教程[M]. 北京:高等教育出版社,1999.
Long Yuqiu,Bao Shihua. Course of Structural Mechanics[M]. Beijing:Higher Education Press,1999(in Chinese).

