考虑参数和线型不确定性的水文设计值估计的贝叶斯方法
梁忠民,李 磊,王 军,戴 荣
(1. 河海大学水文水资源与水利工程科学国家重点实验室,南京 210098;2. 河海大学水文水资源学院,南京 210098;3. 中国水电顾问集团西北勘测设计研究院,西安 710065)
水文频率分析的主要任务是根据水文样本推求指定设计频率(标准)的设计值,为水利工程设计提供依据,其方法分为参数估计方法和非参数估计方法,但目前国内外均采用参数估计方法.当采用参数估计方法进行水文频率分析计算时,一般认为存在3种不确定性[1]:①水文事件本身存在的自然不确定性;②由于资料短缺及估计方法选择等原因,导致对参数的估计存在着不确定性;③鉴于不论采用哪一种水文统计模型(线型),都缺乏物理依据,仅仅是对客观物理现象的一种拟合,因此线型的选择存在偏差,即线型选择的不确定性.
在国外,Wood等[2-3]首先应用 Bayes理论分析了参数的不确定性,随后又综合考虑了参数和线型选择的不确定性;Kuczera[4]提出了基于Bayes理论的单站/地区信息综合的设计洪水计算方法;Tang[5]假定极值与频率之间服从线性关系,推导了可以根据拟合情况自动设置权重的贝叶斯方法;Kuczera[6]根据 Bayes理论考虑了皮尔逊Ⅲ型(P-Ⅲ)和对数皮尔逊Ⅲ型(LP-Ⅲ)等线型下参数估计的不确定性问题,并采用“重要性抽样法(importance sampling)”搜索参数的后验状态空间,构造设计值的抽样分布,进而给出设计值估计的置信区间.在国内,吴伯贤、梁忠民等[7-8]研究了在水文频率分析中的Bayes应用问题,强调了在单站样本缺乏时考虑参数的地区信息(先验分布)可以降低设计值估计的抽样误差;刘攀等[9]针对线型选择的不确定性问题,研究了贝叶斯因子法在线型选择与线型综合中的应用,并通过统计实验验证了所用方法在一定程度上可以识别样本的真实线型.
基于此,笔者根据贝叶斯理论,分别建立了考虑参数估计不确定性和线型选择不确定性的水文设计值推求方法,再根据全概率公式,提出了同时考虑这2种不确定性影响的水文频率分析方法.作为示例,选用了皮尔逊Ⅲ型(P-Ⅲ)和对数正态(LN)2种线型,通过对某河水文站年洪峰设计值的分析计算,提供了本文方法的应用流程和分析结果.
1 基于参数估计不确定性的水文设计值推求1 方法
1.1 水文极值变量的概率密度函数
在 Bayes框架下,统计分布函数中的参数θ作为随机变量,水文变量Q的分布可看成是给定参数θ下的条件分布,即f(Q θ).依据全概率公式,样本D估计的水文变量Q的概率密度函数可表示为

式中p(θ D)为参数θ的后验概率密度函数,其计算公式为

式中:g(θ)为参数θ的先验分布;l(D θ)为样本的似然函数.水文频率分析计算中的样本一般都是所谓的“非简单样本”,即包括实测样本系列和调查样本系列(如历史洪水),本文采用文献[6]的方法对似然函数描述如下:
以 X = { O,H}代表水文的“非简单样本”,其中,代表实测样本系列,代表调查样本系列,( Q(j2),uj, vj)表示 uj年中水文数据大于 Q(j2)的年数为 vj.针对以上情况,假设样本之间相互独立,Qi(1)(i = 1 ~ n )服从一般水文分布,如 P-Ⅲ分布等;中的 vj服从二项分布,则可以得到

其中

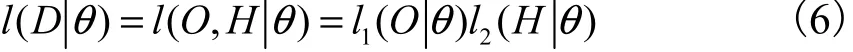
1.2 设计值的推求
由式(1)得设计频率为p的设计值pQ为

2 基于线型选择不确定性的水文设计值推求方法
2.1 水文极值变量的概率密度函数及设计值的推求
本研究根据贝叶斯公式,计算样本属于某一线型的后验概率,以此作为各线型分析结果的权重,再根据全概率公式则可以得到考虑线型选择不确定性条件下的估计值估计方法.
假定样本D属于线型(总体分布模型) Mi的先验概率为 p (Mi) ,则根据贝叶斯公式,其属于线型 Mi的后验概率为

式中:i=1~k,k为备选线型的个数;先验概率p(Mi)在没有特别信息的条件下,按照“无信息贝叶斯先验准则”取1/k;l(D Mi) 表示样本来自模型 Mi条件下的似然函数.
以后验概率p(MiD)对备选的线型进行加权,则根据全概率公式可以得到水文极值变量Q的概率密度函数为
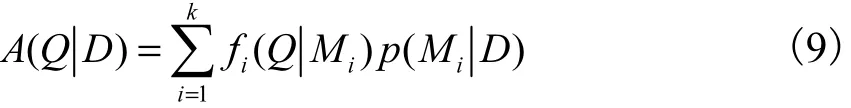
由于式(9)中仅考虑线型选择的不确定性,所以第i种线型的概率密度函数fi( Q Mi) (或其中的参数)可以采用常规的参数估计方法(如适线法或线性矩法等)估计.
由式(9)得指定设计频率p的设计值pQ为
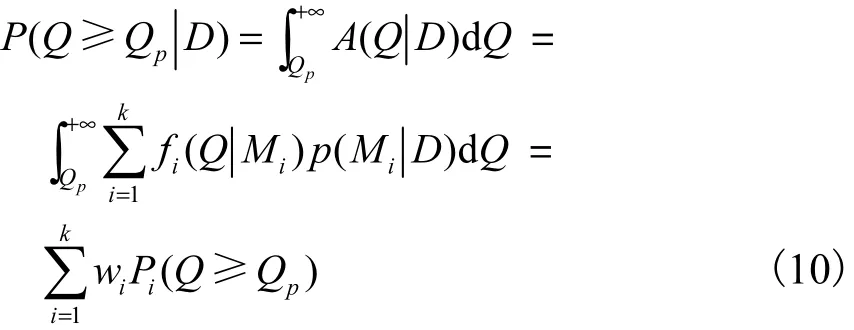
式中:wi为对线型 Mi的加权,wi= p(MiD);Pi(Q≥Qp)为采用线型 Mi条件下设计值 Qp对应的频率.
2.2 后验概率估计
由式(10)可见,推求设计值的关键在于计算各线型的后验概率p(MiD),本文采用贝叶斯因子法对p(MiD )进行估计[10].
记 Bji代表任意 2个备选线型似然函数的比值(也称为贝叶斯因子),且有

将jiB代入式(8)得

因此,只要估计出贝叶斯因子的值就能计算出各线型的后验概率p(MiD )值,进而可根据式(10)得到设计值估计.贝叶斯因子的计算式为

3 综合考虑参数估计和线型选择不确定性的设计值估计方法
3.1 水文极值变量的概率密度函数及设计值的推求
上述研究中,只分别涉及了给定样本条件下参数估计或线型选择的不确定性对设计值估计的影响问题,实际的水文频率分析计算中包含了这2种不确定性的共同作用,根据全概率公式,本文提出综合考虑参数估计和线型选择不确定性的设计值估计方法.
水文极值变量Q的概率密度函数可以表示为

式中:Ii(Q D )的意义类同式(1),反映的是参数估计的不确定性;p(MiD)表示样本D属于线型 Mi的后验概率,反映的是线型选择的不确定性;φ( Q D)是同时考虑参数和线型这 2种不确定性情况下水文极值变量的概率密度函数.
根据式(14),指定设计频率p的设计值pQ为

3.2 设计值估计的数值算法
从式(7)和式(15)可以看出,直接推求设计值时需要复杂的积分运算,求解困难.为避免积分运算,本研究采用基于“马尔可夫链蒙特卡罗(Markov chain Monte Carlo,MCMC)”方法,通过随机抽样方式推求设计值.MCMC方法的基本思想是建立马尔可夫链对参数进行抽样模拟,根据 MCMC方法不仅可以获得设计值的各类点估值(如期望值估计),同时也可以得到设计值的抽样分布,据此也可以对设计值估计的不确定性做出定量评估.在众多 MCMC算法中,自适应 Metropolis(adaptive Metropolis,AM)抽样应用最为广泛.相比传统的 MCMC算法,AM 不再需要事先确定参数θ的推荐分布,而是由后验参数的协方差矩阵来估算,且后验参数的协方差矩阵在每一次迭代后自适应地调整,具体做法详见文献[11-12]介绍.作为例子,本文设计的基于 MCMC抽样技术求解式(15)的算法如下.
(1)运用MCMC法对式(2)中的参数θ进行随机抽样,进而构造各线型参数θ的后验分布.
(2)根据式(13)计算贝叶斯因子,再由式(12)确定各线型权重wi= p(MiD).
(3)根据各线型的权重{w1,… ,wk},随机抽选一个线型i.
(4)利用线型i参数θ的后验分布,随机抽出参数的一个样本,代入线型i的概率密度函数,进而推求出某一频率下的洪水设计值 Qp.
(5)重复以上步骤(3)~(4)m次,得到一系列洪水设计值 Q1p, … ,Qpm.
(6)对上述的设计值系列进行统计,即可获得设计值的点估值(如期望估计值);同时,也可得到对估计的不确定性评价,如估计方差或某一置信水平的置信区间等特征量.
4 计算实例
4.1 资料情况
某河水文站实测洪峰流量资料[13]共30年,历史特大洪水 2年,历史考证期 102年,如表 1所示.根据前述确定样本似然函数的方法,将历史特大洪水归为 H 类,即(2,520,102,1)和(2,200,102,2),其余实测洪峰流量都归为O类.

表1 某水文站洪峰流量观测系列Tab.1 Observations of peak flow at the studied gauge m3/s
4.2 设计值估计
本研究选择了 P-Ⅲ和 LN两种常用的总体分布作为备选线型.
1)考虑参数估计不确定性的设计值估计
在本例中,由于缺乏研究断面洪峰流量统计参数的区域信息,所以,采用贝叶斯理论中的“无信息贝叶斯先验准则”,将各统计分布参数的先验分布取为其取值范围内的均匀分布.对 P-Ⅲ型:作为例子,均值的取值区间为实测系列中的最大、最小值,vC的取值区间为[0.3,1],sC 的取值区间为[0.6,4];对 LN 型:均值u的取值为[5.0,8.0],σ的取值区间为[0.1,1.0].同时采用MCMC算法,可以得到各统计分布参数的后验分布直方图,如图1和图2所示.根据这些参数样本,可以获得设计值的抽样分布,基于该分布就可以得到设计值的点估计及区间估计,表2列出了设计值的期望值、变差系数、90%置信区间以及置信区间的离散度(定义为置信区间变幅与期望值之比).本计算实例表明,随着设计频率的减小(设计标准的提高),设计值的变差系数和置信区间的离散度都在增大,表明设计标准越高,估计的不确定性越大;相同设计频率下,P-Ⅲ型分布的估计不确定性略小于LN分布估计的不确定性.

图1 P-Ⅲ型参数后验分布直方图Fig.1 Parameter posterior distribution histograms of P-Ⅲ distribution

图2 LN分布参数后验分布直方图Fig.2 Parameter posterior distribution histograms of Lognormal distribution

表2 设计值估计结果Tab.2 Estimation of design values
2)考虑线型选择不确定性的设计值估计
对给定的样本系列,采用式(11)~式(13)可得备选线型的后验概率,以此作为各线型的概率加权权重,P-Ⅲ线性的权重为0.52,LN的权重为0.48;再由式(10)可得考虑线型选择不确定性的设计值估计,见表3,同时给出P-Ⅲ和LN经验适线法结果,以便对比.
计算结果表明,对研究的样本系列,选择P-III分布的概率略大于选择LN分布的概率.
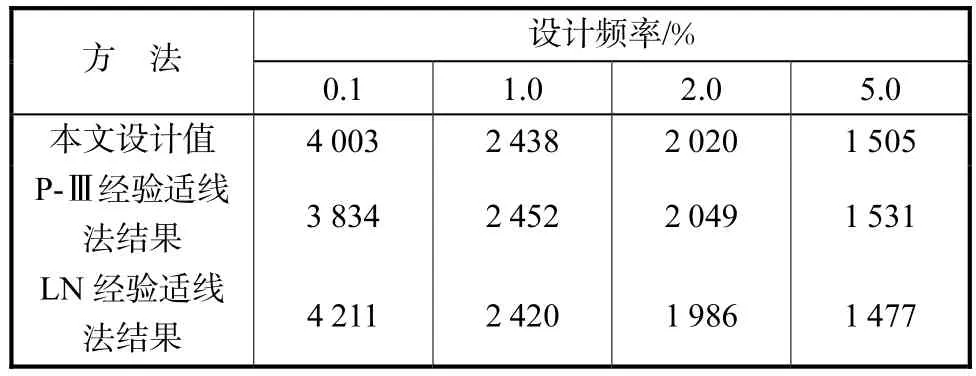
表3 考虑线型不确定性的设计值及经验适线法结果Tab.3 Design values considering model uncertainty and those of empirical curve-fitting method m3/s
3)同时考虑参数估计和线型选择不确定性的设计值估计
根据式(15)的MCMC算法,给出了综合考虑线型参数和线型选择不确定性的设计值估计结果,见表2;图3提供了本文方法与经验适线法的频率曲线对比,并显示了按照本文方法估计的90%置信区间.
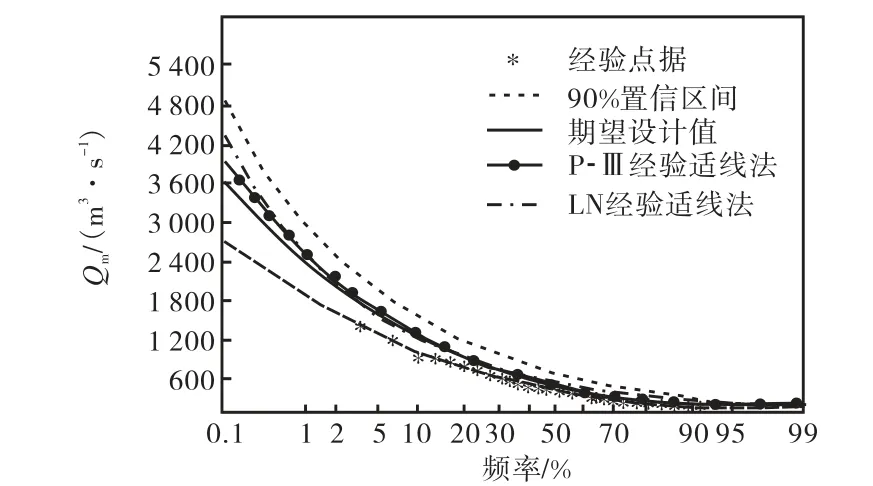
图3 Bayes方法与经验适线法的频率分析结果Fig.3 Frequency analysis results of Bayesian method and empirical curve-fitting method
4)结果分析
将表 2中的 2种方法的设计值变差系数和置信区间离散度数值单独列于表 4.其中,第 3列是同时考虑参数估计和线型选择不确定性的结果;第4列是只考虑参数估计不确定性的结果(以表 2中 P-Ⅲ和LN结果的平均值表示);第5列是只考虑线型选择不确定性的结果,由下列方法求得.
在给定样本条件下,水文设计值估计的不确定性是由线型选择或参数估计的不确定性引起的,而线型选择和参数估计可以认为是相互独立的,所以,根据数理统计原理,设计值估计的总误差(以离差平方和表示)应等于线型选择误差()与参数估计误差()之和,据此,可以根据表4中第3列和第4列的“设计值变差系数”求得第5列中的相应数值.

表4 设计值估计不确定性对比Tab.4 Comparison on uncertainties of design value estimation
由表 4中数据可知,同一设计频率下,不管是设计值变差系数还是置信区间离散度,同时考虑线型选择和参数估计不确定性的数值都大于只单独考虑参数估计不确定性或线型选择不确定性时的数值.这说明,只单独考虑参数估计或线型选择的不确定性,都不能对设计值估计的不确定性做出完整的评价.另外,随着设计频率的减小(设计标准提高),这种差值变大,说明估计的不确定性在增大.对比分析只考虑参数估计不确定性和只考虑线型选择不确定性两种情况的结果表明,前者的设计值变差系数和置信区间离散度整体上都大于后者的相应数值,说明对本计算样本,参数估计的不确定性是引起设计值估计不确定性的主要因素.
5 结 论
(1)根据 Bayes原理和全概率公式,分别推导了单独以及同时考虑线型选择和参数估计 2种不确定性情况下的设计值计算公式.
(2)通过采用MCMC抽样技术进行设计值估计,可以获得设计值估计的抽样分布.由该抽样分布不仅可以得到设计值的点估值,如期望值估计,也可以对估计的不确定性进行定量评价,如设计值估计的偏差系数、置信区间等.
(3)实例结果表明,给定样本条件下,从完整描述估计不确定性的角度,应该采用同时考虑参数估计和线型选择不确定性的频率分析方法.
(4)本文计算实例中参数的先验分布取为均匀分布,仅是一个示例,有其局限性.在实际的水文频率分析工作中,可以获得设计断面临近站点或区域的洪水分布或统计参数信息,将这些信息作为设计断面的先验信息,从而对先验分布做出估计,使得根据后验分布作出的估计结果将更加合理.
[1] Benjamin J R,Cornell C A. Probability Statistics and Decision for Civil Engineers[M]. New York:McGraw-Hill,1970.
[2] Wood E F,Rodriguez-Iturbe I. Bayesian inference and decision making for extreme hydrologic events[J]. Water Resources Research,1975,11(4):533-542.
[3] Wood E F,Rodriguez-Iturbe I. A Bayesian approach to analyzing uncertainty among flood frequency models[J].Water Resources Research,1975,11(6):839-843.
[4] Kuczera G. Combining site-specific and regional information:An empirical Bayes approach[J]. Water Resources Research,1982,18(2):306-314.
[5] Tang W H. Bayesian frequency analysis[J]. Journal of the Hydraulics Division,1980,106(7):1203-1218.
[6] Kuczera G. Comprehensive at-site flood frequency analysis using Monte Carlo Bayesian inference[J]. Water Resources Research,1999,35(5):1551-1557.
[7] 吴伯贤. 贝叶斯方法在洪水频率分析中的应用[J]. 成都科技大学学报,1990(1):68-74.
Wu Boxian. Bayesian approaches to inference of probabilities of extreme hydrologic events[J]. Journal of Chengdu University of Science and Technology,1990(1):68-74(in Chinese).
[8] 梁忠民,丛树铮. 水文频率分析中的一种贝叶斯方法[J]. 河海大学学报,1994,22(1):7-12.
Liang Zhongmin,Cong Shuzheng. A Bayesian method in hydrological frequency analysis[J]. Journal of Hohai University,1994,22(1):7-12(in Chinese).
[9] 刘 攀,郭生练,田向荣,等. 基于贝叶斯理论的水文频率线型选择与综合[J]. 武汉大学学报:工学版,2005,38(5):36-40.
Liu Pan,Guo Shenglian,Tian Xiangrong,et al. Selecting and averaging of flood frequency models based on Bayesian theory[J]. Engineering Journal of Wuhan University,2005,38(5):36-40(in Chinese).
[10] Kass R E,Raftery A E. Bayes factors[J]. Journal of the American Statistical Association,1995,90(430):773-795.
[11] Haario H,Saksman E,Tamminem J. An adaptive metropolis algorithm [J]. Bernoulli,2001,7(2):223-242.
[12] Gelman A,Rubin D B. Inference from iterative simulation using multiple sequences [J]. Statistics Science,1992,7(4):457-511.
[13] 詹道江,叶守泽. 工程水文学[M]. 3版.北京:中国水利水电出版社,2000.
Zhan Daojiang,Ye Shouze. Engineering Hydrology[M]. 3rd ed. Beijing:China Water Conservancy and Hydropower Press,2000(in Chinese).

