一类弹簧复合振子系统行波解的运动复杂性

刘洁，胡艳霞，张洪光

（1.华北电力大学数理学院，北京102206；2.赤峰学院数学学院，内蒙古赤峰024000）

一类弹簧复合振子系统行波解的运动复杂性

刘洁1，胡艳霞1，张洪光2

（1.华北电力大学数理学院，北京102206；2.赤峰学院数学学院，内蒙古赤峰024000）

本文研究了一类弹簧复合振子系统行波解的运动复杂性，借助Melnikov函数方法讨论了该系统产生smale马蹄意义下混沌的可能性及成因，并结合顺行平面Hamilton周期-能量关系和KAM理论，给出受扰系统固有周期运动的理论解释.文中结论可为研究弹簧复合振子在机械装置中的应用提供一定的理论依据.

弹簧复合振子；混沌；Melnikov函数；KAM理论

近些年来迅速发展起来的混沌理论[1，2]等非线性系统理论，为解决复杂的非线性问题带来了希望.文献[3]研究了具有两种不同阻尼的线性弹簧振子运动情况，通过分析和数值计算方法求解其运动规律，得到了传统的采取空气阻力与速度的关系是线性关系在某些情况下是不符合实际的.文献[4]研究了一类非线性系统——弹簧摆耦合振荡器系统的动态，得到了该系统会发生分叉运动.

本文对一个典型的非线性系统——弹簧复合振子系统做了一定的理论分析，展示了弹簧复合振子系统行波解的运动复杂特性.首先建立了这类弹簧复合振子的运动微分方程，然后运用Melnikov函数方法[5]对该系统行波解发生混沌现象进行解析.也尝试结合KAM理论[6，7]和顺行平面Hamilton系统的周期-能量关系[8]对该系统的准周期运动状态及稳定性进行了理论证明.

1 数学模型和运动微分方程

我们考虑只作扭曲运动的水平弹簧上个吊着N振子的运动，振子在垂直于弹簧的水平面内转动，由角动量定理，则第i个振子的运动方程[9]，I，其中I为振子的转动惯量，φ为振子偏离平衡位置的夹角，K为弹簧的扭曲常数，F是重力产生的恢复力.设第i个振子受到一个很小的外力作用，致使方程右端还有一项-εcoswt，其中w为外力振动频率.则第i个振子的运动方程为

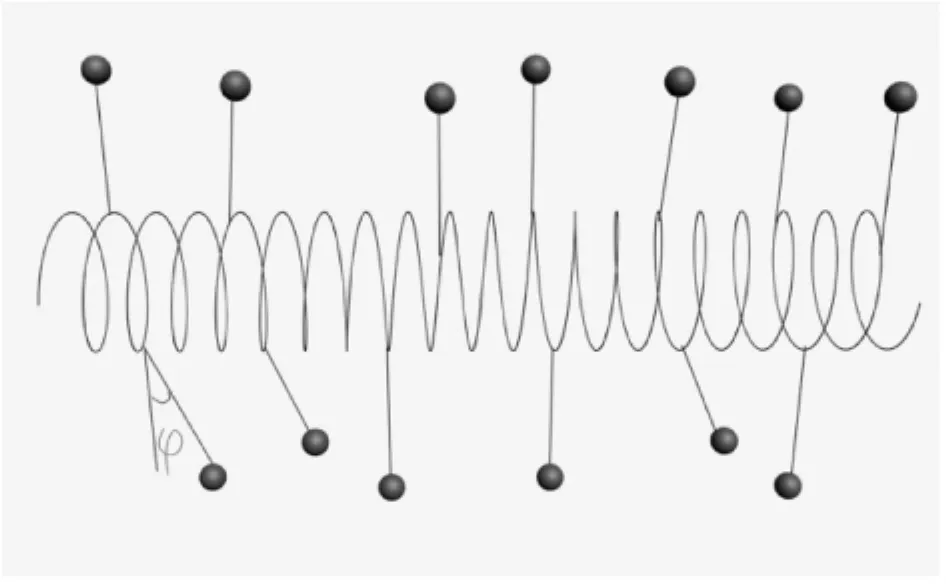
图1 水平弹簧上吊着N个振子

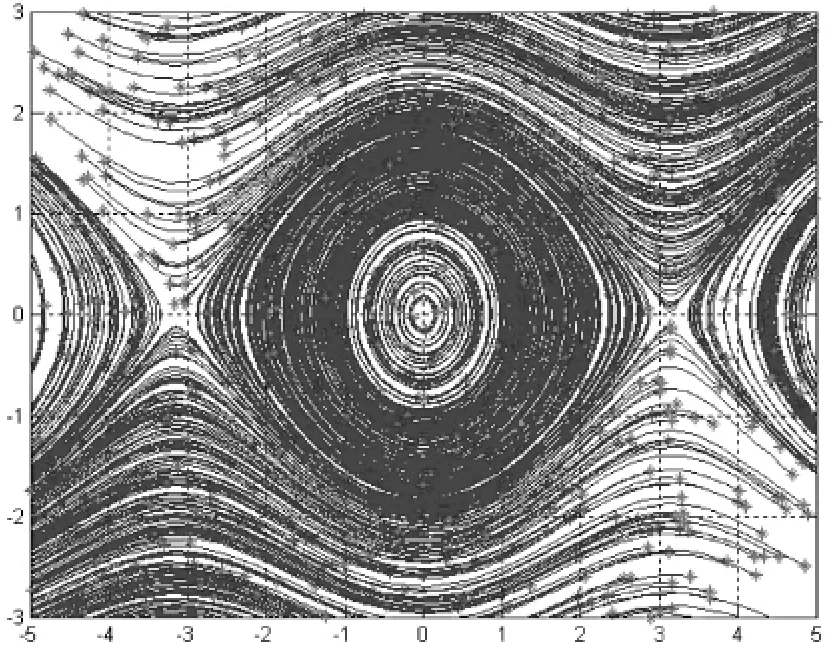
图2 时系统（6）的相图

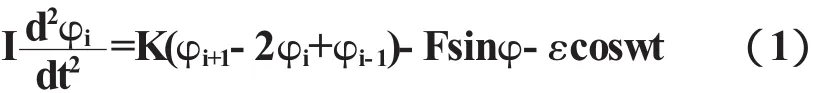
假设相邻两振子的距离是△x，则（1）可以写成

当λ>0，在(u,v)相平面上，系统（6）有平衡点(2kπ,0)，(±π+2kπ,0)，这里k为整数.由于平衡点的分布具有周期性，我们可以在一个周期内考虑，-π≤u≤π.该系统有三个平衡点A-(-π,0)O(0,0)，A+(π,0)，由微分方程定性理论[10]可以判断判定，A-和A+是鞍点，而O是中心，系统在平衡位置附近的相图如图2所示.当h=0时，系统退化为中心O，当0

3 受扰系统的动力特性分析

考虑c2>1，即λ>0（6）的动力特性.由前面知道，在ε=0时，系统有异宿轨线，其附近的结构不稳定，受扰后在系统的鞍点附近容易发生Smale意义下的混沌现象.下面用Melnikov函数方法讨论异宿轨附近结构的受扰特性.

定理1当c2>1时，系统（5）在鞍点附近的Poincare映射有一系列的横截异宿点，因此也就具有Smale意义下的马蹄混沌.

下面我们借助非线性KAM理论，对中心闭轨线的受扰特性及稳定状态进行理论界定和分析.

应用KAM理论需满足：未扰系统闭轨线的周期解析依赖于轨道；中心奇点附近Poincare映射为扭转映射两个必要条件.引入文[8]的相关结论记为引理1.

引理1假设一个Hamilton系统的Hamilton函数满足下面四个条件：（i）H(u,v)在(u,v)某区域内解析;（ii）(u0,v0)为系统的中心奇点；（iii）埚某正数h*，对任何h∈(0,h*)，对应轨道Γh:H(u,v)=h均为包含在区域内围绕中心奇点(u0,v0)的闭轨；(iv)(u,v)≠ (u0,v0)时，成立，则区间h∈(0,h*)的闭轨周期Th关于h解析依赖.

引理2当c2>1时，系统（6）的闭轨Γh的周期Th关于h解析依赖.

证明对系统（6），显然在区间h∈(0,2λ)内，闭轨Γh满足引理1的（i）～（iii），下面证明满足(iv).因

从而闭轨的周期Th关于h∈(0,2λ)解析依赖.

在c2>1的情况下，为研究系统（6）的中心(0,0)附近的映射Poincare映射.引入作用量-角动量坐标(I,φ),令轨道h=H(I)，则轨道沿闭轨Γh的运动频率表达为∧(I)=dH/dI=2π/T(h)，

从而得到频率的变化率为

定理2当c2>1时,有∧'(I)≠0.

证明由文[8]闭轨周期对能量导数的显式关系

令f(u)=sinu-ucosu，u∈(-π,0)U(π,0)，有f'(u) =usinu，故f(u)在定义域内为增函数，且f(0)=0，所以当u∈(-π,0)，f(u)0，所以T'(h)≠0，从而由（7）式得∧'(I)≠0.

定理3对任意小的ε>0，若∧'(I)≠0，即Poincare映射为扭转映射，则扰动系统（6）的Poincare映射有一族具有正Lebesgue测度μ(ε)的不变轨线，并且当ε→0有.这些不变闭曲线周围充满稠密的无理轨道.

4 结论

本文考虑了一类弹性复合振子系统行波解的运动复杂性.通过上面分析，得到在c2>1的情况下系统在鞍点附近会发生Smale意义下的马蹄混沌现象，即此时系统的行波解的运动是无序的；系统在中心附近发生准周期运动，即非扰动系统的大量闭轨几乎都保留了下来，此时系统的行波解几乎做周期运动.文中结论可以为研究一类弹簧复合振子在机械装置中的应用提供一定的理论依据.

〔1〕Ott.Edwart.Chaosindynamicalsystems[M]. London:Cambridge University Press,2002.

〔2〕MorrisW.Hirsch,StephenSmale,Robert Devaney.Differential Equations,Dynamical Systems,and an Introduction to Chaos 2ed[M]. Academic Press,2007.

〔3〕J.Bartos.Linear spring oscillator with two different types of damping[J].Contributed Papers, 2005,Part III 649–654.

〔4〕A.Gonzalez-Buelga,Y.Kyrychko,D.J.Wagg. Bifurcations on a spring-pendulum oscillator[J]. PAMM,2007.

〔5〕V.I.Arnold.Mathematical methods of classical mechanics,2ed[M].New York:Springer-Verlag, 1989.

〔6〕J.E.Marsden,T.S.Ratiu.Introductiontomechanicsandsymmetry[M].NewYork: Springer-Verlag,1994.

〔7〕管克英,雷锦志.顺行平面Hamilton系统的周期—能量关系[J].北方交通大学学报,2001,25(6): 61-65.

〔8〕高普云.非线性动力学[M].长沙:国防科技大学出版社,2005.

〔9〕谷内俊弥,西原攻修.非线性波动[M].北京:原子能出版社,1981.

〔10〕王高雄,常微分方程[M].北京:高等教育出版社, 2006.

〔11〕庄圻泰,张南岳.复变函数[M].北京:北京大学出版社,1984.

O175

A

1673-260X（2010）11-0003-03

中央高校基本科研业务费专项资金资助（09ML55,09QL49）