关于正六边形旋转对称群的研究

董鸿飞

（赤峰学院物理与电子信息工程系，内蒙古赤峰024000）

关于正六边形旋转对称群的研究

董鸿飞

（赤峰学院物理与电子信息工程系，内蒙古赤峰024000）

本文简要描述了正六边形旋转对称群——D6群,通过对正六边形的旋转运动的分析，得到正六边形的旋转对称群的群表，并对正六边形旋转对称群的性质进行了分析，列出D6群的特征表.

群；群元；群表；特征标

1 引言

尽管物理学中有许多复杂的细节,但仍然存在着很多优美之处及简单性,这多是来源于物理系统的对称性.对称性在物理学中起着重要的作用.对称的概念和变换密切联系在一起.所谓系统的对称性是指它对某种变化保持不变的性质.保持系统不变的变换越多，系统的对称性就越高.群的概念出现于十九世纪初,早期只是一种物理学家研究对称性十分有效的数学工具,但很快有物理学家发现了它在物理学中有着很多用处.1890年Federov和1891年Schoenflies相继用群论方法系统地解决了晶体分类问题,总结出230种空间群.空间群理论自建立以来,在解释晶体结构、对晶体进行分类、帮助人们加深对哈密顿方程解的理解、简化哈密顿本征方程的求解等方面,起到巨大的作用.

2 正六边形旋转对称群的构造

本文只简单讨论正六边形的旋转对称群：

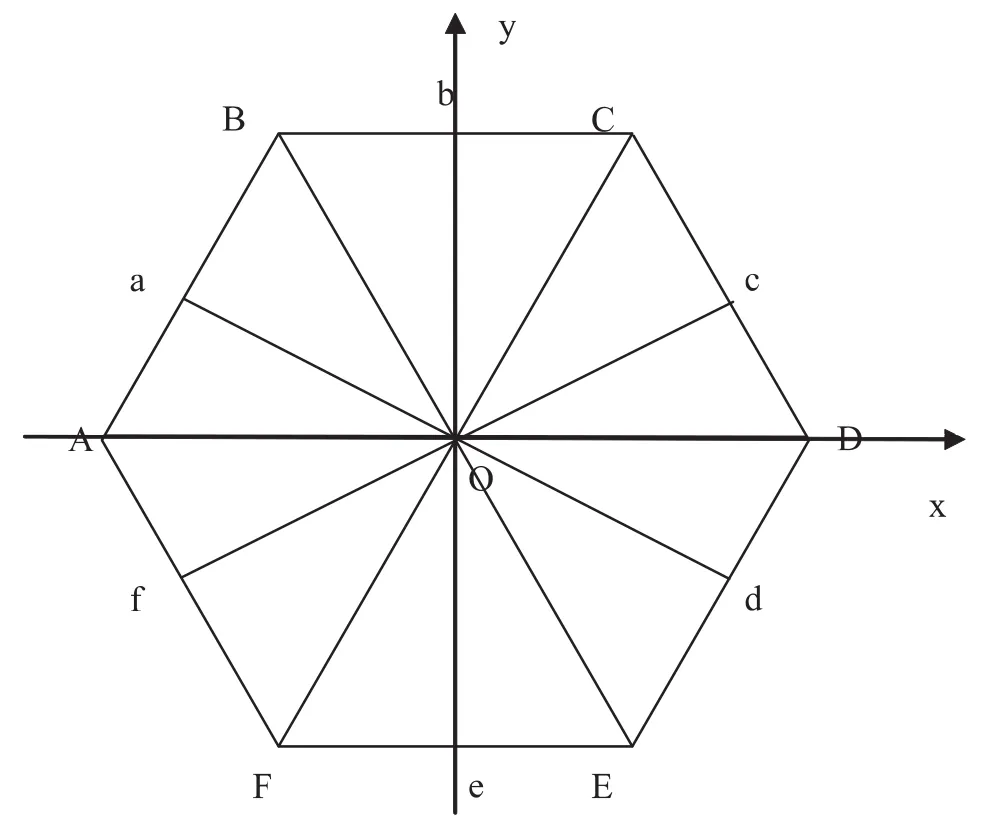
图1

正六边形有6个顶点,6条边,如图1所示正六边形ABCDEF.联结对边的中心，得到线段ad,be,cf.对于正六边形ABCDEF分别以其3条对角线AD,BE,CF为轴，规定顺时针方向为旋转正方向，用ma,mb，mc表示绕三个轴正向转动π的变换.

以正六边形的3对对边的中心连线ad,be,cf为旋转轴,用md,me，mf表示绕轴正向转动π的变换.

以垂直于正六边形的平面且过正六边形中心的直线为旋转轴Z，用C6，C62，C63，C64，C65表示绕Z轴转动π/3,2π/3, π,4π/3,5π/3的转动.

以上述12个元素为群元建立的群，为正六边形的旋转对称群，命名为D6群.

3 正六边形的旋转对称群群表

正六边形的12个群元，分别为C6，C62，C63，C64，C65、ma、mb、mc、md、me、Mf.则正六边形的旋转对称群群表如表1：

4 正六边形旋转对称群的性质

D6群为正六边形旋转对称群,有12个群元,所以D6群是12阶群.这12个群元可以分六类,分别是

5 正六边形旋转对称群表示的构造

点的坐标的变换，变换前的坐标记作（x,y）,变换后的坐标记作(x',y'),他们都用列矩阵表示，而变换元素表为2×2矩阵

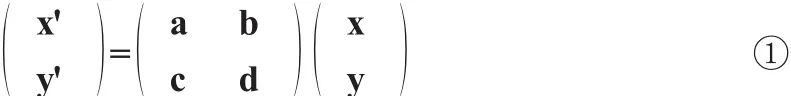
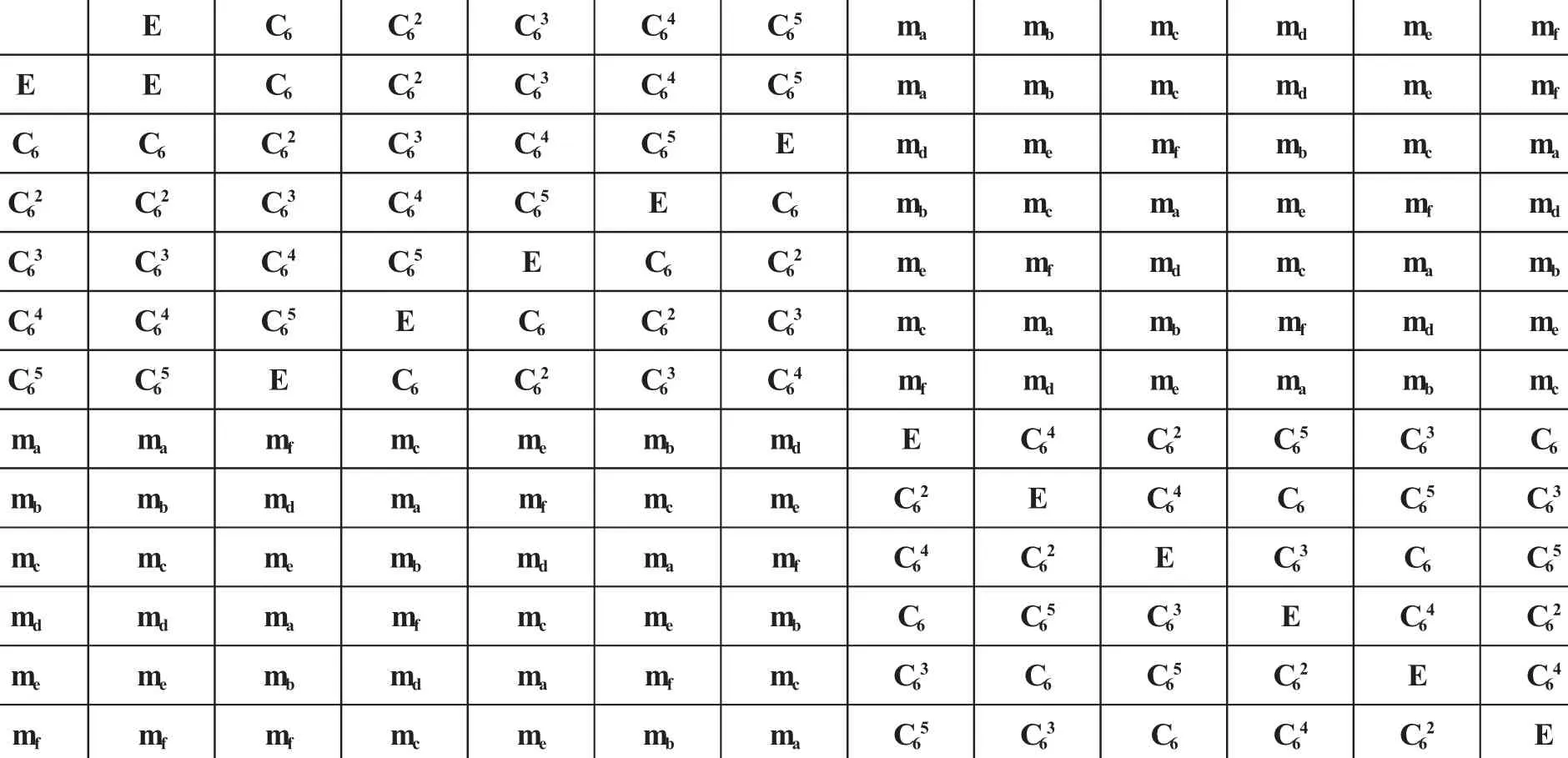
表1

对每一个变换，把变换前后正六边形的顶点坐标代入①式，就可定出群元素对应的矩阵形式.

例如：变换ma把B点变换到F点，把C点变换到E点，于是有等式：

6 正六边形旋转对称群的特征标表

D6群有12个群元，有六个自逆类，由12+12+12+12+22+22=12知，它有四个一维、两个二维不等价不可约的自共轭表示.得到D6群的特征标表如下：

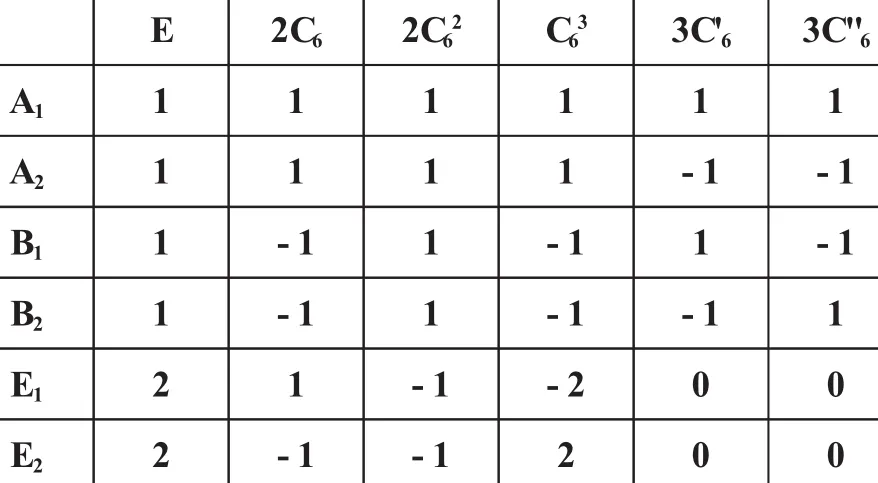
E2C62C62C633C'63C"6A1111111 A21111-1-1 B11-11-11-1 B21-11-1-11 E121-1-200 E22-1-1200

〔1〕马中骐.物理学中的群论（第二版）.科学出版社，2006.

〔2〕A·W·约什.物理学中的群论基础.科学出版社，1986.

〔3〕陈金全.群表示论的新途径.上海科学技术出版社，1984.

〔4〕俞文海.晶体结构的对称群.中国科学技术大学出版社，1991.

O711

A

1673-260X（2010）11-0010-02