AHP 与0-1整数规划在招聘中的应用研究

● 董福荣 叶欣逢

AHP 与0-1整数规划在招聘中的应用研究

● 董福荣 叶欣逢

层次分析法是人才测评的重要方法，本文通过对定性与定量因素进行综合处理,并针对其无法解决条件约束问题提出了用层次分析法和0—1整数规划法相结合构建出人才招聘模型，最后试图通过案例证明该模型的有效性与科学性。

层次分析法 0-1整数规划 招聘

人才是组织生存和发展的第一要素，而招聘作为人力资源管理的第一步，其质量如何直接影响人力资源管理的有效性。成功的招聘、招聘质量的提高会大大促进组织人力资本的积累和增长。

科学的人才测评是帮助寻找和识别合适人才的有效方法。20世纪70年代美国运筹学家T·L· Satty经过深入研究，运用定量与定性相结合的系统分析方法，提出了层次分析法(AHP—Analytic Hierarchy Process)，这种方法不仅弥补了以往测评中的不足，而且被证明在行为目标结构复杂且缺乏必要数据情况下更为实用。但是，决策者在做出录用决策时仍然要受到一系列要素——特别是资源的限制，如工资成本、员工数目、员工平均年龄、公司形象（学历等问题）等，而通过0-1整数规划方法的运用则会有效解决招聘过程中条件约束的问题。因此，两种方法结合起来是解决招聘中主观愿望与客观现实相互矛盾的有效方法。

基于上述分析，本文借鉴有关理论提出了用AHP和0-1整数规划相结合的方法来解决组织招聘问题，为人才选拔和配置提供了一种比较可靠的计算方法。

一、招聘模型的建立

首先，建立招聘模型，通过专家评定，用AHP方法确定各备选人员的权值；其次，利用该权值结合约束条件构建出AHP和0-1整数规划结合模型，由此确定最优人选。

（一）层次分析法（AHP）

层次分析法解决问题的思路如下图：

1.建立层次结构模型

AHP的关键在于建立层次结构模型。根据系统分析方法，结合所要解决的问题和达到的目标对系统因素和层次的分析，进而设计系统层次结构的表示模型。招聘过程中涉及的因素很多，选择时要考虑各因素的重要性、影响力或者有限程度等，选取差异较大、放弃条件基本相同的因素，建立准则层和方案层。如图1，录用权重为目标层A，选择知识面、理解能力、应变能力、表达能力等作为准则层C，N个应聘者作为方案层P，据此建立层次结构模型。

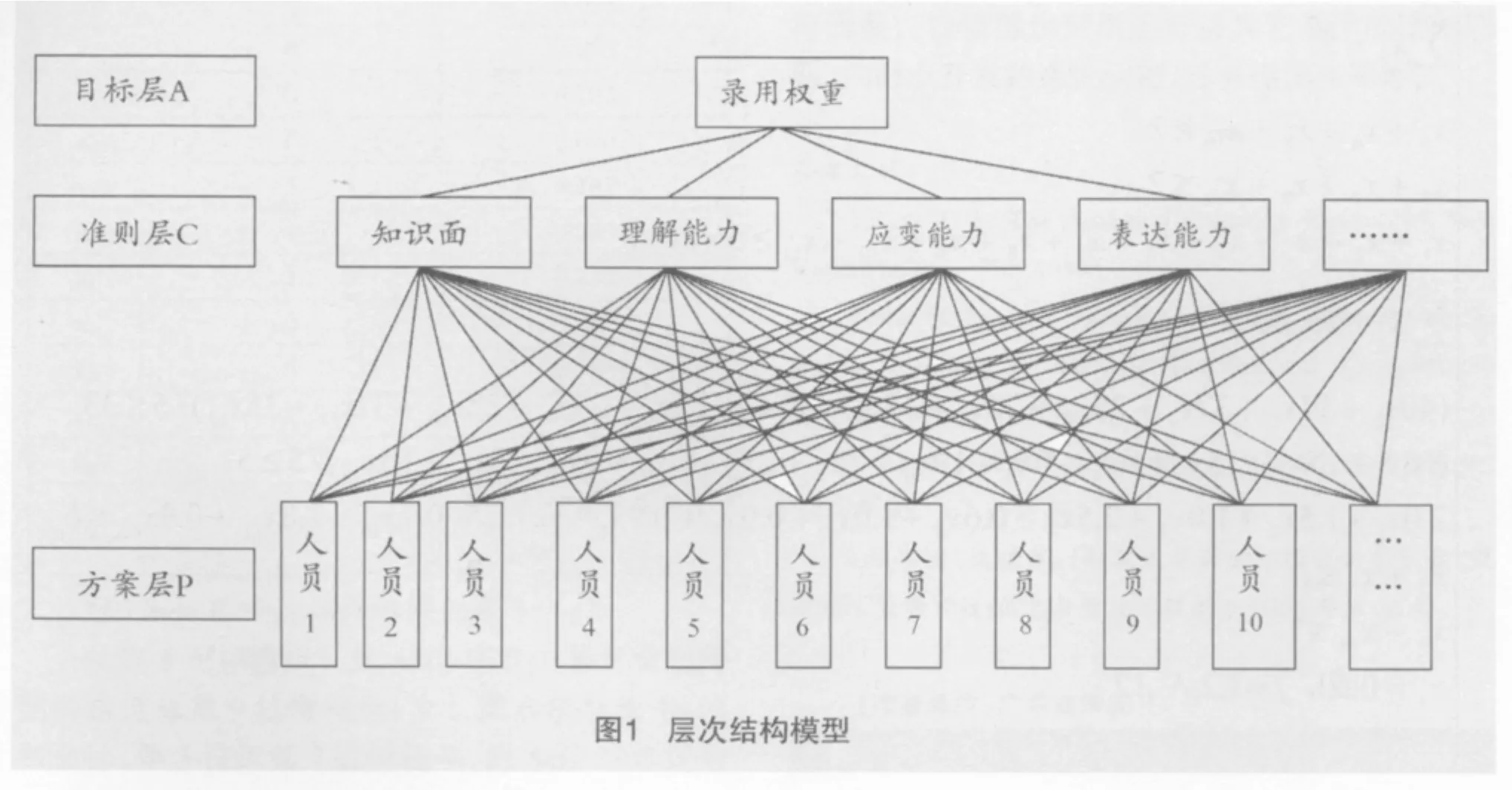
2.构造各层判断矩阵

任何系统分析都以一定的信息为基础，基于人们对客观事实的认识，对每一层次各元素的相互重要性作出判断，并标值量化，进而构造出判断矩阵，这是AHP的关键一步。判断矩阵主要是对上层次某要素而言，说明本层次与之相关的各要素之间的相对重要程度。

3.层次单排序及其一致性检验

层次单排序是根据判断矩阵计算对于上层某元素而言，是基于本层次与之有联系元素的重要性次序的权值。它是对本层次所有的元素针对上一层次而言的重要性进行排序的基础，即求出权重。判断矩阵仅仅是专家对实际情况作出主观判断的数值矩阵，一般来说，这种判断能力可能是不准确的，或者存在较强的主观性。因此，有必要检验判断矩阵是否满足一致性的标准。当CR≤0.1时，判断矩阵满足了一致性要求，否则由于判断矩阵偏离一致性程度过大，而必须考虑对判断矩阵进行重新修订以满足判断矩阵的要求。

4.层次总排序并作出决策

利用上一步对同一层次中所有层次单排序的结果，即每一层元素对其上一层各要素的相对权重，再进一步计算出层次分析模型中的每一层中所有要素相对于目标层的组合权重；根据权重的大小，判断各方案的优劣，从而为选择最优方案、使整个系统达到最优化提供决策依据。同理，层次总排序也需通过一致性检验，否则需要进一步调整判断矩阵直至满足一致性。

通过在教材中渗透“数学建模思想”，培养学生的数学应用意识与能力。在教学内容的安排上考虑：第一，让学生认识到每一个数学概念、公式、定理。从广义上说都是数学模型，如从实例中抽象出导数概念即给这类问题建立了数学模型；第二，让学生了解数学建模的方法和过程。教材从经济函数关系的确定到经济问题的建模求解，应给出分析和说明；第三，课程末另设专篇介绍综合运用数学知识建模的几个范例，培养学生初步应用数学建模的创造能力，同时为参加数学建模大赛做好准备。

应用AHP方法能够有效提高招聘选拔的科学性和合理性，但是由于没有考虑到约束条件的限制，得到的结果可能与实际差距较大。为了弥补这一不足，我们认为，人才招聘选拔录用可采用AHP和0-1整数规划方法相结合的模型。

（二）0-1整数规划

在整数规划中有一类特殊情形，它的变量仅能取0或者1，这时的xi成为0-1变量，这类问题也就是0-1整数规划。而在人员招聘中，由于是有n个人和n个职位，并由AHP方法知道第i个人被录用做第j个职位的录用权重为wij，i=1,2Λ N；j= 1,2Λ R（在招聘过程中，wij可能为能力权重，使得总录用权重最大），要求在招聘过程中使得总录用权重最大，才能保证招聘到的员工整体能力最强，因此其成为最优模型如下：

设xij为决策变量，则有：

目标函数：

约束条件：

二、案例分析

（一）用AHP法求得各个应聘人员的录用权重

某单位招聘科长、秘书、会计等五名人员，在初试中，使用层次分析法的原理，建立如图1递阶层次结构，目标层为录用权重（能力值）；准则层为知识面、理解能力、应变能力、表达能力、言谈举止；方案层为各个应聘人员。经过专家打分构成各层次判断矩阵，通过计算分别给出各个录用权重值（能力值）。如表1（包括个人应聘人员的基本资料）：

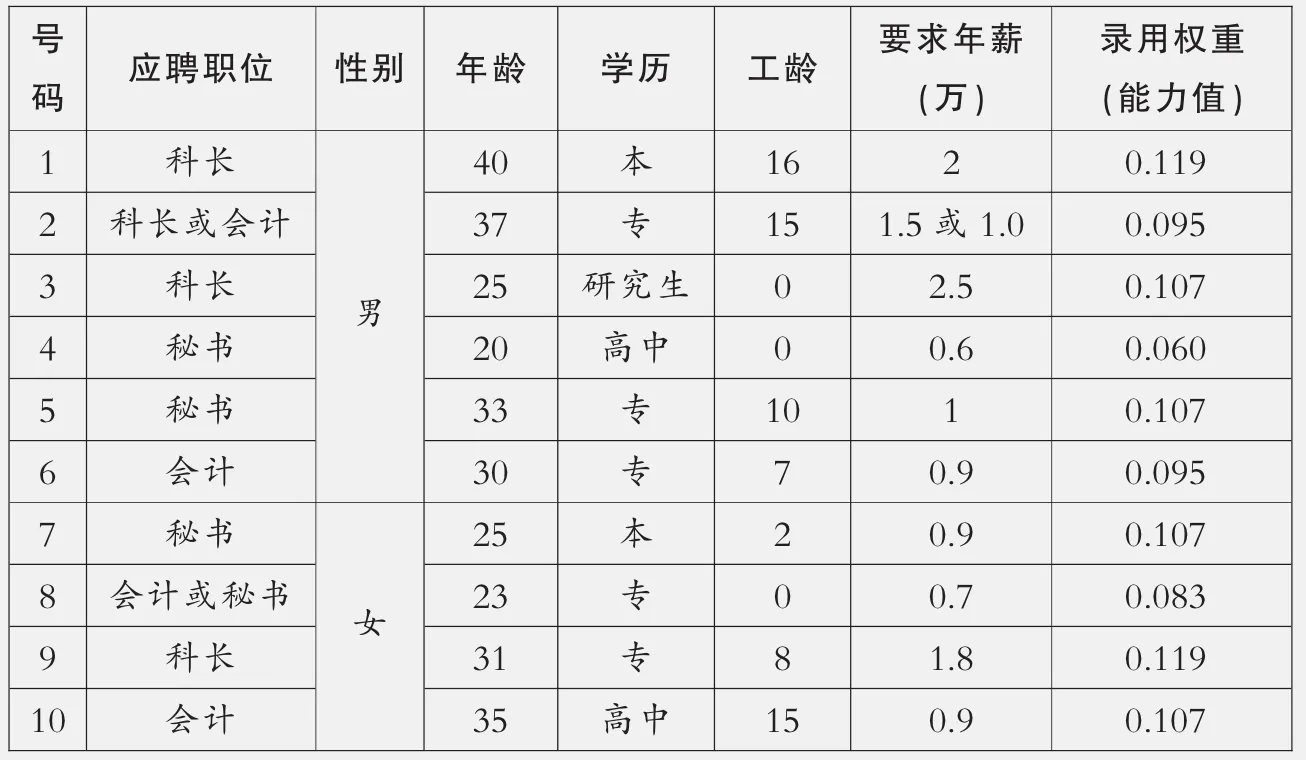
表1

现要求：

①秘书至少招聘二人

②会计不超过二人

③科长招聘一人

④专科及专科以上学历不低于80%

⑤女性比例不低于40%

⑥平均年龄不超过33岁

⑦应聘人员年薪总额不超过6万元

⑧每人最多只能占据一个职位

问：应聘请哪些人，使既能满足要求，又使整体录用权重最大（能力最高）？

（二）用AHP与0-1整数规划模型得出最优方案

首先，假设变量，如表2：

表2

可建立如下模型：

经Lindo软件计算得结果如表3：

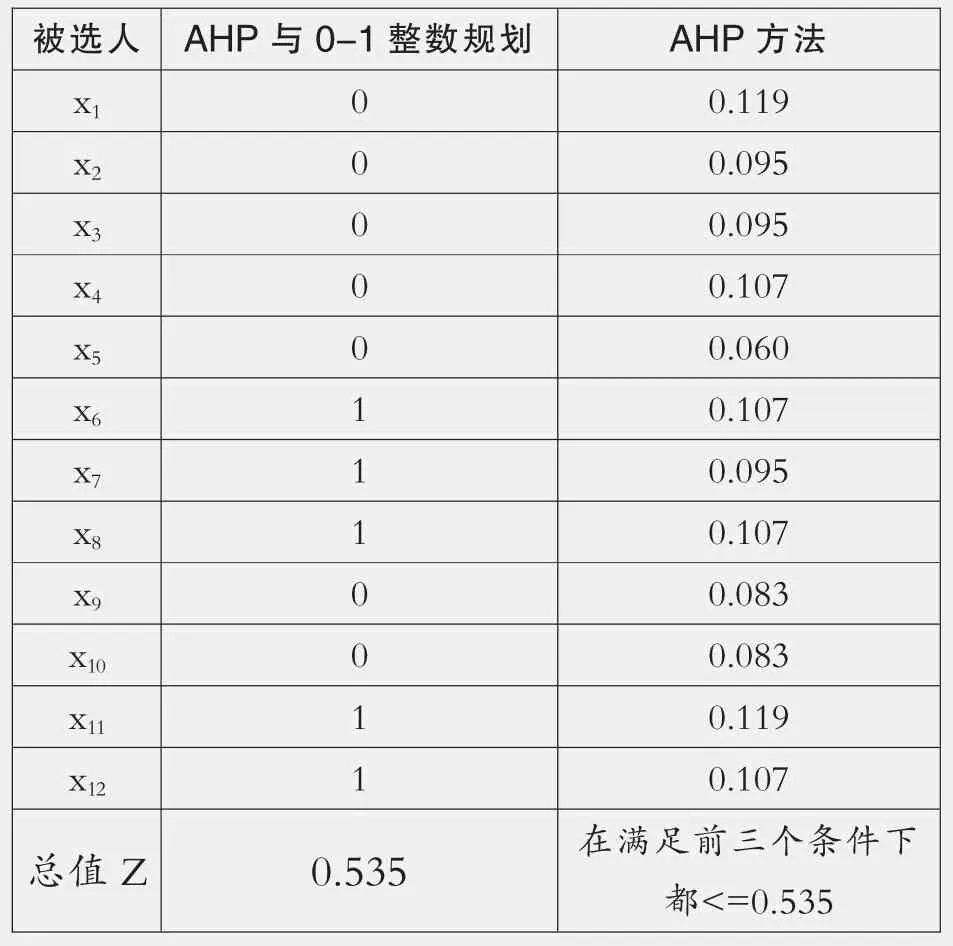
表3

从表3可以看出，经AHP和0-1整数规划得到的是选择第9位做科长（女）、第6位与第10位做会计、第5位和第7位做秘书，而AHP方法在前三个条件（录用五名，包括秘书至少两人、会计不超过两人、科长一人）得到的总体录取权重（能力值）不管怎样组合都小于或等于0.535，因此用AHP和0-1整数规划结合的模型求解，既可达到目标值，又能满足约束条件，实现最优求解。

综上所述，运用层次分析法和整数规划方法相结合来解决组织招聘中的人才选拔问题，充分体现了层次分析法在处理多目标、多准则、问题复杂等方面的优点，并把0-1整数规划处理条件约束的能力引入到该方法中。通过案例分析，表明该方法能较优地解决这类带有条件约束的选拔，是求解此类问题的有效方法。但是,考虑到运用该方法所得出的人才录取权重（能力值等）的大小会直接影响招聘效果，而且直接关系到能否通过一致性检验，所以利用层次分析方法确定权重时，要广泛征集有关人员和专家的意见。使得所计算出的权重较好地符合实际情况，从而最大限度地提高该模型的适用性。此外，根据待解决问题的实际情况，对评价指标进行调整，该模型也可用于解决其它类似的选择问题，如网点开发的选址问题，任务指派问题等。

1.Satty T.L.The Analytical Hierarchy Process[M].New York：McGraw-Hill，1980.

2.Min H.Location planning for airport facilities using the analytic hierarchy process [J].Logistics and Transportation Review，1994，30(1):79-94.

3.李荣钧：《模糊多准则决策理论与应用》，科学出版社，2002年版。

4.陈中文、饶从军：《科技成果的模糊综合评价》，载《武汉理工大学学报(信息与管理工程版)》，2004年第26期。

（作者单位：广东商学院）

■责编一心 Tel:010-68345891 E-mail：cqzlfr@163.com