ARIMA模型在城市年用电量预测中的应用

张士强，王 雯，王 健

（1.山东科技大学，山东 青岛 266510；2.泰山集团，山东 泰安 271000）

ARIMA模型在城市年用电量预测中的应用

张士强1，王 雯1，王 健2

（1.山东科技大学，山东 青岛 266510；2.泰山集团，山东 泰安 271000）

介绍了单整自回归移动平均模型（antoregressive integrated moving average model，ARIMA）及其建模思路，并结合Eviews软件将ARIMA模型应用于成都市年用电量的分析与预测。经检验此模型预测精度较高，拟合效果理想，体现了应用ARIMA模型进行用电量预测的可行性，可以为电力系统工作人员进行年用电量预测提供参考。

ARIMA；用电量预测；偏相关函数；自相关函数

用电量预测是电力系统调度与运营的重要任务，预测的准确程度，关系到国民经济、社会安定、居民生活及电力公司本身的发展。本文介绍了单整自回归移动平均模型，并给出了使用这一模型进行建模和预测的一般过程，而后进行了实证分析，通过建立相应的ARIMA模型，分析预测年用电量。

近年来，利用ARIMA模型对各行业时间序列进行预测的研究越来越多。文献［1］根据中国农产品贸易数据特点，构建了中国农产品进出口的ARIMA模型，对中国农产品进出口进行预测，得到的平均预测误差仅为3.291%和3.248%，达到了最小方差意义下的最优预测效果；文献［2］对中国能源消费总值数据序列进行分析，建立了中国能源消费的ARIMA模型，检验结果表明，ARIMA模型对原始数据序列有着较好的拟合效果；文献［3］利用ARIMA模型对土耳其主要燃料能源消费进行了预测，结果显示模型拟合效果理想；文献［4］建立ARIMA模型对售电价格进行预测，得出的短期预测效果优于长期预测效果。近年来，关于用电量预测的研究越来越多；文献［5］将一种新的灰色模型应用于城市年用电量预测中，在工程实践中具有一定的应用价值；文献［6］以华北电网月度售电量为基础，运用季节ARIMA模型进行分析，结果表明，该方法对售电量的短期预测有较高的预测精度。本文对成都市1950—2007年的年用电量的时间序列进行统计规律分析，结合统计软件Eviews，建立成都市用电量的ARIMA模型，以此来预测用电量的发展变化，具有一定的参考价值。

1 ARIMA模型概述［7］

时间序列模型是由博克斯·詹金斯1976年提出的。这种建模方法的特点是不考虑其他解释变量的作用，仅依据变量自身的变化规律，利用外推机制描述时间序列的变化。时间序列模型一般分为4种类型，分别是自回归过程、移动平均过程、自回归移动平均过程和单整自回归移动平均过程。

如果一个线性随机过程可表示为

式中：φi，i=1，…，p，为回归参数；ut为白噪声过程。则该过程为p阶自回归过程，记为AR（p）。

如果一个线性随机过程可表示为

自回归移动平均过程，是由自回归和移动平均2部分共同构造的随机过程，记为ARMA（p，q）。其中p、q分别表示自回归分量和移动平均分量的最大滞后阶数。它的表达式为

以上介绍了3种平稳的随机过程。当时间序列非平稳时，首先要通过差分使序列平稳后再建立时间序列模型。随机过程yt若经过d次差分后可变换为一个平稳可逆的ARMA（p，q），则称yt为（p，d，q）阶单整自回归移动平均过程，记为ARIMA（p，d，q）。ARIMA过程用Φ（L）Ddyt=θ0+Θ（L）ut表示，式中：Φ（L）和Θ（L）分别为p阶自回归算子和q阶移动平均算子；θ0为漂移项；Ddyt表示对yt进行d次差分后的平稳过程。它包括了单整的AR、MA和ARMA过程。

根据博克斯·詹金斯的建模思想［8］，建立时间序列模型通常需要以下步骤：

（1）数据预处理

在建模之前首先进行平稳化检验，判断是否为平稳序列，可以通过相关图判断。如果一个随机过程是平稳的，则其自相关函数呈指数衰减或正弦衰减，而且衰减得快；相反，如果是非平稳过程，则衰减得很慢。也可以用单位根检验（Dickey⁃Fuller test，DF检验）以及扩展DF检验（augmented Dickey⁃Fuller test，ADF检验），判断随机过程的平稳性。单位根检验是检验时序稳定性的一种正式的方法。若为非平稳序列，则通过差分变换、对数变换、季节差分对数据进行平稳化、均值化处理［9］。

（2）模型的识别与定阶

模型的识别主要依赖于对时间序列的相关函数（autocorrelation function，ACF）图与偏相关函数（partial autocorrelation function，PACF）图的分析：ACF图表现为拖尾衰减特征，而PACF图在p期后出现截止特征，则该过程适合AR（p）；ACF图在q期后出现截止特征，而PACF图表现为拖尾衰减特征，则该过程适合MA（q）；ACF图与PACF图都呈拖尾衰减特征，则该过程是ARMA。

通过图形分析选择模型的形式并初步确定p、q的值。同时利用赤池信息量准则（Akaike information criterion，AIC）和施瓦兹准则（Schwarz criterion，SC）对多种ARMA（p，q）模型进行对比与筛选，选出最优的ARMA（p，q）。

（3）参数的估计

对AR（p）模型的参数进行普通最小二乘法（or⁃dinary least squares，OLS）估计，而MA（q）和 ARMA（p，q）采用迭代式的非线性最小二乘法进行估计。

（4）模型的诊断与检验

模型的诊断与检验包括被估参数的显著性检验和残差的随机性检验。如果估计的模型中的某些参数不能通过显著性检验，或者残差序列不能近似为一个白噪声序列，则需再次对模型进行识别。

（5）模型的预测［7］

2 实证分析——以成都市为例

以成都市1950—2007年的历年用电量［10］为样本，利用统计软件Eviews对成都市1950—2005年的年用电量数据建立ARIMA模型，预测2006—2010年的用电量。2006—2007年的数据留作模型检验数据，用于同预测值比较，评价预测精度。

2.1 数据预处理

将原始数据记为x，作出其线形图，如图1所示。

智能变电站装配式建筑造价评价模型的合理构建重点在于探索科学的方法解决多个造价影响因子的群决策问题，本文在基于造价因子的识别基础上，提出的直觉梯形模糊数多因子群决策方法，能够更加细腻准确的刻画专家对影响因子的确定、不确定、犹豫度三种状态，同时，能够通过测度专家个体偏好与专家群体平均偏好的距离科学解决专家权重完全未知的问题。

图1 序列x折线图

从图1中可以看出，成都市的年用电量逐年上涨，曲线向右上方陡直倾斜，前后增长幅度不一致，呈指数增长趋势，很显然该数据不平稳并且存在异方差，所以先对数据取对数，以消除异方差，生成新序列LNX=lnx，并对LNX进行1阶差分，得DLNX序列如图2所示。

图2 序列DLNX折线图

从图中可看出，通过对序列进行差分处理，数据的趋势性已被消除，时间序列已基本平稳。再次通过Eviews对序列DLNX进行ADF检验。ADF检验的一般模型结构为式中：ut为白噪声［2］。零假设为H0∶γ=0；备择假设为H1∶γ＜0。接受零假设意味着该序列含有单位根，即该序列为非平稳序列［2］。检验结果如表1所示。

表1 DLNX单位根检验结果

由表1知1阶差分序列在1%、5%或10%的显著水平下，均拒绝原假设，接受不存在单位根的结论，因此该时间序列是平稳的时间序列，取d=1。

2.2 模型的识别与定阶

DLNX序列滞后12期的ACF图和PACF图如表2所示。

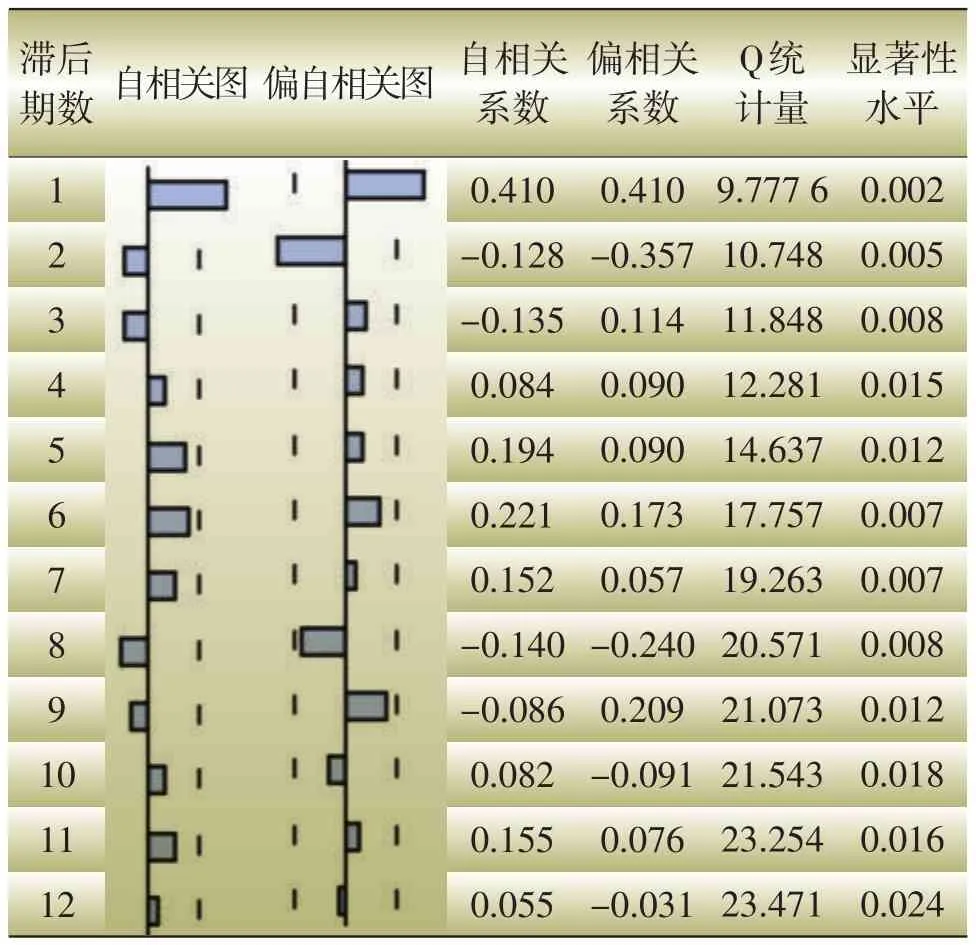
表2 DLNX序列滞后12期的ACF图和PACF图

由表2可以看出，该序列的ACF图和PACF图都是拖尾的，所以判断出此序列适合ARMA模型。图中虚线之间的区域为自相关或偏相关中正负2倍与估计标准差所夹成的。如果相关值在这个区域内，则在显著水平为5%的情况下显著不为0。其自相关函数在1阶处出现峰值并迅速衰减，偏相关函数在1、2阶显著不为0。所以初步选定模型为ARMA（2，1）。但这只是粗略估计，有较大主观性。

2.3 模型的建立

运用非线性最小二乘法中的迭代算法，借助Eviews对ARIMA（2，1，1）进行参数估计。具体结果见表3。

表3 模型估计结果

估计结果显示：模型ARIMA（2，1，1）中C、AR（1）、AR（2）、MA（1）的系数都显著异于0，模型是比较显著的。模型的复相关系数为0.291 993，修正复相关系数为0.248 646，回归标准为0.214 419，残差平方和为2.252 799，对数似然估计量为8.486 398，DW统计量为1.981 934，被解释变量均值为0.135 062，被解释变量标准为0.247 367，AIC信息量为-0.169 298。AR特征根的倒数为0.15+0.48i，0.15+0.48i；MA特征根的倒数为-0.31。特征根的绝对值都大于1，所以该序列为平稳序列。AIC=-0.169 298，较小的AIC值代表较高的拟合优度。可以初步确定ARIMA（2，1，1）是较为合理的。从而得到接下来对残差序列进行白噪声检验。根据初步确定的模型对序列进行回归拟合，如图3所示。图中实际值与拟合值基本一致。模型的残差图如图4所示。从图4中可以看出，残差序列类似白噪声序列，非常平稳，没有明显的趋势性，模型拟合效果比较好［2］。

图3 模型拟合折线图

图4 残差折线图

表4 模型残差序列滞后12期的ACF图和PACF图

对残差序列进行ADF检验，如表5所示。ADF值为-5.327 009，而在1%显著水平下，ADF的临界值为-3.562 669，因此序列在1%显著水平下被看作白噪声序列，模型的拟合值是实际值的无偏估计，模型拟合效果比较好。

表5 模型残差序列ADF检验结果

2.4 模型的预测

由ARIMA（2，1，1）模型，可得lnXt的预测公式为：

用ARIMA（2，1，1）对2006—2010年成都市用电量进行预测，预测结果见表6。其中2006—2007年的相对误差分别为1.5%和6.0%。这说明预测值与实际结果是比较接近的，预测精度比较高。模型对2008—2010年用电量进行预测，从预测结果看出，用电量仍然保持持续上涨趋势。

3 结束语

通过对1950—2005年成都市年用电量序列进行分析和所建立的模型检验结果表明，本文建立的ARIMA（2，1，1）模型对原始数据序列有着较好的拟合效果，模型的预测效果比较理想。但从2006—2007预测结果的相对误差随时间越来越大可以看出，该模型对于短期预测较合理，但对于长期预测，模型有一定的缺陷［11］。说明了ARIMA模型用于用电量预测的可行性，可以为电力系统工作人员进行年用电量预测提供参考。但是不同地区电力需求量的变化规律不甚相同，需要对原始数据进行深入分析后确定合适的模型参数才能使预测结果更符合实际。

表6 2006—2010年成都市用电量实际值与预测值

：

［1］汪艳涛，王记志.中国农产品贸易ARIMA模型的建立及预测［J］.经济与管理，2009（7）：11-15.

［2］杨伟传.中国能源消费的ARIMA模型预测分析［J］.统计与决策，2009（11）：71-72.

［3］Ediger V，Akar S.ARIMA forecasting of primary energy demand by fuel in Turkey［J］.Energy Policy，2007，35（3）：1701-1708.

［4］Contreras J.ARIMA models to predict next⁃day electrici⁃ty prices［J］.IEEE Transactions on Power Systems，2003，18（3）：1014-1020.

［5］李咏凯，张建华，王国栋，等.一种新的灰色模型在城市年用电量预测中的应用［J］.现代电力，2010（4）：13-16.

［6］崔和瑞，王娣.基于季节ARIMA模型的华北电网售电量预测研究［J］.华东电力，2009（1）：70-72.

［7］张晓峒.计量经济学基础［M］.天津：南开大学出版社，2004.

［8］Pankratz A.Forecasting with univariate Box⁃Jenkins mod⁃els：concepts and cases［M］.Greencastle：Depauw Uni⁃versity Press，1984.

［9］何书元.应用时间序列分析［M］.北京：北京大学出版社，2004：86-121.

［10］成都市统计局.成都市统计年鉴2008［M］.北京：中国统计出版社，2008.

［11］吴怀宇.时间序列分析与综合［M］.武汉：武汉大学出版社，2004：58-79.

［12］Greene W H.Econometric Analysis［M］.5th ed.New Jersey：Prentice Hall，2002：11-15

［13］张晓峒.Eviews使用指南与案例［M］.北京：机械工业出版社，2006.

Application of ARIMA model in forecasting annual city electricity consumptions

ZHANG Shi⁃qiang1，WANG Wen1，WANG Jian2
（1.Shandong University of Science and Technology，Qingdao 266510，China；2.Taishan Group，Taian 271000，China）

This paper briefly presented the principles and methods of ARIMA（auto regression moving average）model and applied the model to the analysis and forcasting of electricity de⁃mand of Chendu city.Upon examination it is further proved that ARIMA has high prediction accuracy and provides ideal forecast effect.It’s feasible to use ARIMA model to forecast electricity de⁃mand.The model provides reference for power system staff to fore⁃cast.

ARIMA；electricity demand forcast；partial au⁃tocorrelation function；autocorrelation function

TM715；F407.61

A

1009-1831（2010）06-0031-04

2010-08-02；修回日期：2010-09-03

张士强（1962—），男，山东梁山人，教授，博士生导师，研究方向为企业成本管理；王雯（1987—），女，山东泰安人，硕士研究生，研究方向为信息管理与信息系统；王健（1987—），男，山东泰安人，本科，研究方向为电气工程及自动化。